5 Elastostatics
5.1 INTRODUCTION
In this chapter we will study elastostatics problems assuming that we
have linear material behaviour and neglecting any changes in
orientation of the body due to displacements. In what follows we will
use the indicial notation for brevity.
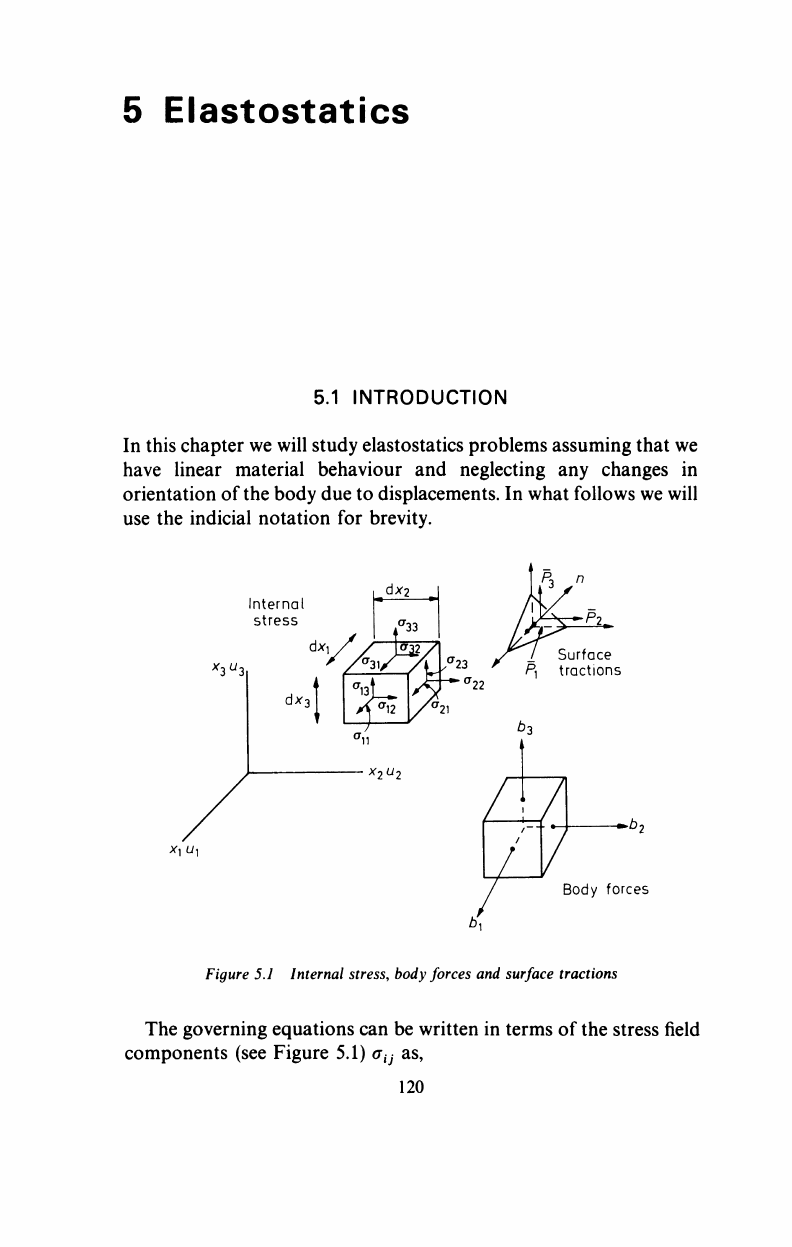
Internal
stress
*3
U
3
*1"1
Body forces
Figure 5.1 Internal stress, body forces and surface tractions
The governing equations can be written in terms of the stress field
components (see Figure 5.1) a
u
as,
120

ELASTOSTATICS 121
δσ
η
θσ
12
δσ
ί3
ϋ—
+
^—
+
~ä—
+
bl =ü
tfXi 0Χ
2
ν
χ
3
^ + ^ + ^ +
ί>
2
= 0 (5.1)
öx
x
dx
2
cx
3
θσ
3ί
δσ
32
θσ
33
+
&
3
= 0
cbcj δχ
2
<3χ
where σ
21
=
σ
12
,σ
31
=
σ
139
σ
32
= σ
23
.
Equations (5.1) can be written in indicial notation, simply as
pl + b
t
= 0 i= 1,2,3 )=l,2,3 (5.2)
OXj
The prescribed surface force intensities or tractions on the surface
Γ
2
of the body are denoted by
p
h
p
2
,p
3
(Figure 5.1). Equilibrium on
the boundary requires the satisfaction of the following boundary
conditions:
Pi =σ
11
Μ
1
+<7
12
Μ
2
+ σ
13
η
3
= ρ
1
Pi = σ
21
η
1
+σ
22
η
2
+ σ
23
η
3
= Ρι (5.3)
P3 = σ
31
«
1
+σ
32
η
2
+ σ
33
η
3
= p
3
where n
l
, n
2
, n
3
are the direction cosines of the normal with respect to
the x
1?
x
2
,x
3
axes, i.e.
n
x
= cos(n,x,) (5.4)
Equations (5.3) can be written in indicial form as,
Pi = Gijitj = ^ i = 1,2,3 7 = 1,2,3 (5.5)
The displacement field is defined by the three displacement
components u
l9
u
2
,u
3
. Let Γ
ί
denote the portion of
the
boundary on
which displacements are prescribed. The displacement constraints
there are,
W
= Mi, U
2
=M
2
, U
3
= Ü
3 /c
,.
or
γ ι 2 ό ό
(5.6)
Ui = U
t
.
The
üi
are the prescribed values. Note that the total surface Γ of the
body is equal to Γ
ι
+Γ
2
.

122 ELASTOSTATICS
The strains
at
any point are defined
by the ε
0
·
components
of
the
strain tensor, which
in
indicial form are,
i=l,2,3
7 = 1,2,3 (5.7)
The strains
and
stresses
are
related
by the
constitutive relations
which
for an
isotropic body are,
- du
k
(du
t
du:
/iBftv
,, =
A
,-
+
,^
+
^j (5.8)
where
δ
ί}
is
the Kronecker delta and Λ,,μ are Lame's constants which
can also
be
expressed
in
terms
of the
modulus
of
elasticity
E and
Poisson's ratio
v by,
E
E
A =
(l + v)(l-2v)'
μ =
2(ΓΜΟ
(5,9)
Sometimes
μ is
written
as G,
which
is the
shear modulus.
In certain problems different effects, such
as
temperature,
can be
included
as
initial stresses
or
strains.
If
the effects are considered
as
initial stresses
we
have,
.
?
du
k
/du: du:
n
= oj
+
°?j
(5.10)
where
a
{j
are now elastic stresses, equal to total stresses σ^ and the
σ°
components. Note that
σ° for a
thermally isotropic material
is
σ£=-Λε?^ (5.11)
For
a
temperature problem
the ε£ are
ε?·
= αΓ
(5.12)
where
a is
the dilatation coefficient and
T
the difference
in
tempera-
ture. The effect of initial stresses or strains can be analysed in the same
way
as
body forces.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
