Matrices
If your work is a system of equations, you work primarily with the coefficients of the terms of the equations. If you organize the terms of an equation so that their variables are in a standard order, then you arrive at the representation of systems of equations you have worked with so far in this chapter. Consider, for example, a system along the lines of the following:
3x - 4y = 1
5x + 2y = 19
You can proceed to solve the system of equations for the x and y values by using the approach given in the previous section. At the same time, you can use an approach that involves using matrices. A matrix consists of an array or collection of numbers. In a matrix, you organize the numbers in a rectangular fashion, in rows and columns. Matrices are always identified according to their rows and columns. If a matrix contains 2 rows and 3 columns, then it is said to be a 2 × 3 matrix. If a matrix contains 2 rows and 2 columns, then it is said to be a 2 × 2 matrix.
Mathematicians usually identify matrices by enclosing them in square brackets. They identify the elements within by using letters with subscripts or by providing the numbers themselves. A 3 × 3 matrix might be represented this way:
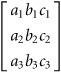
A 2 × 2 matrix might be represented this way:
A vast and interesting field of study investigates the behavior of matrices, and the use of matrices in programming related to the graphics for computer game development and the logic of games involves matrices extensively. In this context, matrices provide an alternative approach to solving the system of equations.
If you examine the coefficients of the system of equations given above, you see that you can create a 2 × 3 matrix. In other words, the matrix consists of 2 rows and 3 columns. You can write it as follows:
If you work with a set of three equations with three variables for which you want to find values, you might start with this set of equations:
x - y + 5z = -6
3x + 3y - z = 10
x + 3y + 2z = 5
This becomes the basis of a 3 × 4 matrix, which you present in this way:
When a variable has no visible coefficient, implicitly its coefficient is 1. You use this fact when you create a matrix to represent a system of equations. Implicit coefficients appear as 1. Along the same lines, negative coefficients remain negative.
One further point is that you can combine equations with different numbers of variables. For example, a system similar to the one just shown might take the following form:
x - 5z = -6
3x + 3y - z = 10
3y + 2z = 5
When you translate such a system of equations into a matrix, to preserve the orders of the variables, you insert zeros. Here is how you represent such a system:
1 0 -5 -6
3 3 -1 10
0 3 2 5
In this system of equations, you account for the missing y and x variables in the first and third equations by inserting zeros.
Note
In the discussion in this chapter, the enclosing square braces that often characterize matrices do not appear. This is a measure taken to make the presentation of the matrices easier. For general purposes, enclosing braces is often regarded as a matter of personal preference.
Working with a 2-by-3 Matrix
A matrix provides a convenient way to systematically solve for the values of a system. Your activity in this respect proceeds in the same way that it did when you worked with systems of equations and left the variables visible. When you work with matrices, however, you work with a system that consists of rows and columns, and the goal of your activity is to arrive at matrices that take the following form:
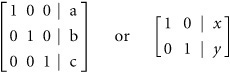
Accordingly, for each row in the matrix, you proceed with multiplication and addition activities, as you did in the previous section, and your goal is to eliminate all values save those that correspond to one of the columns and the final column. The final column provides you with a variable value.
The system of equations presented in the previous section appears as follows:
3x - 4y = 1
5x + 2y = 19
The matrix you create using its coefficients assumes this form:
To solve for the values of this matrix, you begin by examining the first row and determining a value that allows you to transform the 3 into 1. This value is the multiplicative inverse of 3, which is
. Accordingly, when you carry out this multiplication, you arrive at this matrix:
You can then proceed to evaluate the second row. Your goal is to discover the number by which you can multiply the first row in order to eliminate a column. You seek a number that allows you to transform the first row so that you can add it to the second and eliminate the value (5) in the first column. This number is -5. Accordingly, your work proceeds in this way:
You then add the first row as transformed to the second row:
Your matrix now assumes this form:
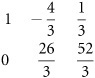
At this point, you evaluate the second row to discover a way to reduce the value in the second column to 1. To accomplish this, you can multiply the elements in the row by
, the multiplicative inverse of
. Here is the form this activity assumes:
You now have a new matrix, which appears this way:
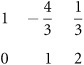
Your target now becomes finding a way to eliminate the second column value from the first row. To accomplish this, you multiply the second row by a number that transforms it so that when you add it to the second row you eliminate the target value. This number is
. To carry out these activities, you proceed in this way:
Given this transformation of the second row, you add it to the first:
Your matrix now assumes its final form:
1 0 3
0 1 2
Given this matrix, you can identify the solutions of the system as x = 3 and y = 2.
Exercise Set 11.7Here are some systems of equations to transform into matrices and solve for two values.
|
Working with a 3-by-4 Matrix
To work with 3 × 4 matrices, you follow the same path you follow with 2 × 3 matrices. The only difference is that a few more steps are involved. Consider, for example, this system of equations:
x - y + 5z = -6
3x + 3y - z = 10
x + 3y + 2z = 5
If you transform this into a 3 × 4 matrix, you assign values of 1 to the appropriate coefficients and drop the variables:
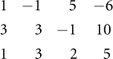
To develop a solution set for this matrix, your goal involves arriving at a matrix that possesses this form:
For each row, then, you seek to transform the values so that you see a 1 and a corresponding value.
For the current matrix, the first column of the first row is already set to 1, so you can shift your attention to the second row. You find a value by which you can multiply the first row that allows you to eliminate the first element from the second row. This value is -3. To multiply the first row by this value, your actions take the following course:
You then add the transformed version of the first row to the second row:
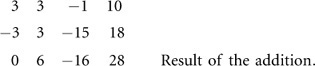
This gives you the following matrix:
1 -1 5 -6
0 6 -16 28
1 3 2 5
The next step involves determining the value by which you can multiply the first row to make it possible to eliminate the first element from the third row. It ends up that you can achieve this goal if you multiply by -1. Accordingly, you carry out the multiplication:
| 1 -1 5 -6 | |
| -1 1 -5 6 | Multiply first row by -1. |
You then add the transformed version of the first row to the third row:
| 1 3 2 5 | |
| -1 1 -5 6 | |
| 0 4 -3 11 | Result of the addition. |
Your rewritten matrix takes this form:
1 -1 5 -6
0 6 -16 28
0 4 -3 11
You now have the first column of the matrix in good form, so you can proceed to work with the second column. Toward this end, you inspect the second row. To transform the second element of this row so that it becomes a 1, you multiply by
. The result of the multiplication is this row:
After you factor the fractions, your matrix assumes this form:
To eliminate the second element from the first row, you can make use of the transformed version of the second row. The value of the second element in the second row is 1, so you do not have to make any changes to reach your objective. You simply add the second row to the first. When you do so, your work takes on this form:
Here is the new matrix:
You now proceed to multiply the second row by -4 to create values that you can add to the third row to eliminate the second element. Here are the activities you perform:
Here is the new matrix:
You can now reach the first of the major goals of your operation, which is to discover the value that corresponds to the third row. Toward this end, you multiply the third row by the multiplicative inverse of
. Here is the matrix that results from this operation:
Given that you know the value of the third element in the third row, you can multiply this row by
to create a set of values you can add to the first row to eliminate the third element from that row. The result of the multiplication is as follows:
When you add this row to the first, your matrix that results takes this form:
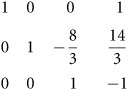
To eliminate the third element from the second row, you multiply the third row by
. The result of the multiplication takes this form:
When you add this to the second row, your matrix then assumes its final form:
1 0 0 1
0 1 0 2
0 0 1 -1
You can write the solution values for this matrix as x = 1, y = 2, and z = -1.
Exercise Set 11.8Here are some systems of equations with three values that you can solve using matrices.
|