Degrees and Radians
When you first learn to relate an angle to a circle, your activity often begins with an orientation toward the circle that begins with the Cartesian plane. As Figure 12.6 illustrates, you extend a line (r) from the center of a circle to its perimeter. Using the standard form of an angle, you identify the x axis extending to the right from the origin as the initial side of the angle. The line that creates the angle constitutes the terminal side. You measure the angle (θ) created by the initial side and the terminal sides in degrees that describe the perimeter of the circle.
Figure 12.6. Degrees of a circle allow you to measure angles.
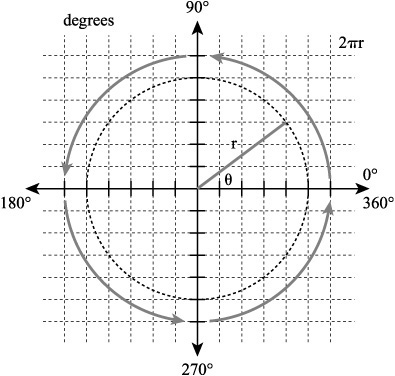
The measure of an angle θ has no maximum value in degrees. If it extends upward from the origin, following the path of the y axis of the Cartesian plane, its measure is 90°. Since the line is perpendicular to the initial side, you call it a right angle. If the line extends to the left of the origin, its measure is 180°, and you call it a straight angle. An angle of 270° follows the y axis downward and is also perpendicular to the initial side. You can call it a right angle, also.
If an angle measures 450°, it is the same as one revolution of the circle plus 90°, so it is a right angle. If an angle measures 540°, it is the same as one revolution of the circle plus 180°, and it is a straight angle. In this respect, if someone tells you to turn a screw 1440° degrees to the right, then, you determine the number of terms by dividing the degrees by the circumference of a circle: 
. The measure of the angle from the initial size to the terminal side is 0. No remainder is left after the division.
Circumference and Radians
The radius of a circle consists of a line extending from the center of the circle to any point on its perimeter. The circumference of a circle is a measure of the arc of a complete circle. To calculate the circumference of a circle, you multiply 2 times π by the radius of the circle. Here is the equation:
C = 2πr
The variable C signifies the circle’ s circumference, while r represents the radius, and π is an irrational number with an approximate value of 3.14. Given this representation of a circle, you can describe a circle in terms of radians.
A radian is an arc on the perimeter of a circle that is equal in length to the radius of the circle. Given the equation C = 2πr, then, there are 2π radians in a complete circle. In other words, if you travel around the circle a distance equal in length to the radius multiplied by 2π, you end up where you started.
A radian is an arc equal in length to the radius of a circle. If you use an approximate value for π of 3.14 and multiply by 2, then you can say that 6.28 radians can be placed head to tail to complete one revolution of a circle.
As Figure 12.7 illustrates, you can relate the size of an angle using radians. The procedure involves using π alone or making π part of a quotient. To accomplish this task, consider how to designate the four directions of the compass using radians. You start to the east. This direction corresponds to the positive direction of the x axis.
Figure 12.7. Radians allow you to readily measure angles.
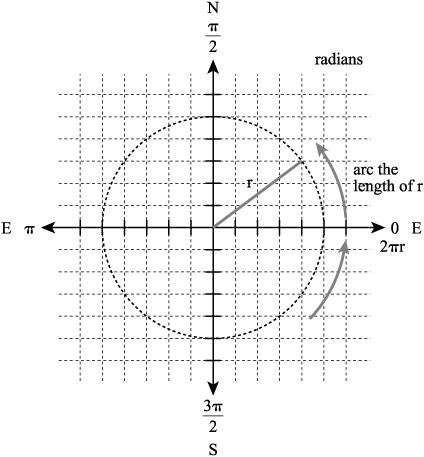
East is usually considered the initial side of angles, so this is at degree 0. The radian value of east is also 0. To now set the compass values for north, west, and south, consider that if a complete revolution of a circle involves 2π radians, then half a revolution (180°—west) involves π radians. If half a revolution involves π radians, then a quarter of a revolution (90°—north) involves radians. When you add 
radians to π radians, you arrive at 3
radians. This is three-quarters of a revolution or an angle of 270°—or south.
Table 12.1 provides you with radian and degree measurements for the angles that represent the cardinal directions of the compass.
| Degrees | Radians | Compass Direction |
|---|---|---|
| 0 | 0 | East |
| 45° |  | Northeast |
| 90° |  | North |
| 135° |  | Northwest |
| 180° | π | West |
| 225° |  | Southwest |
| 270° |  | South |
| 315° |  | Southeast |
Degrees to Radians
To convert degrees to radians, you use this formula:
Here are a few examples of use of this conversion:
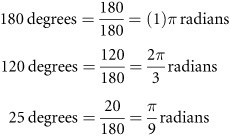
Exercise Set 12.1For each of the following degree measurements, identify the measurement in radians.
|
Radians to Degrees
To convert radians to degrees, you multiply by 
. Here are a few examples:
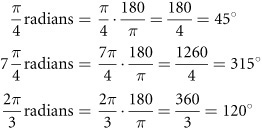
Exercise Set 12.2For each of the following radian values, name the corresponding degree value.
|
