Arbitrary Vertex Positions
In addition to translating the vertex of the parabola along the x axis, you can move it vertically, along the y axis. Toward this end, consider what happens if you add a constant k to the basic quadratic equation you have worked with in the previous sections. Here is the new form of the equation:
a(x – h)2 + k
This form of the equation allows you to adjust the y-intercept of the parabola. When you assign a value to k, you can translate the position of the vertex of the parabola up or down relative to the y axis.
As Figure 9.10 illustrates, if you assign a positive value to k, then you translate the vertex of the equation upward on the y axis. If the value of a is positive, then the vertex of the parabola opens upward, so the coordinates (x, y + k) establish the minimum vertex value. Since k is a positive value, the vertex is translated upward along the y axis.
Figure 9.10. By setting the values of a, k, and h to positive numbers, you position the parabola so that it opens upward in quadrant I of the Cartesian plane.
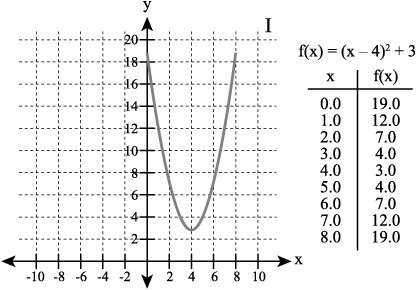
As Figure 9.10 illustrates, since the equation also includes the expression x – 4, the parabola is shifted to the right along the x axis. The vertex lies on the x axis, and the parabola opens up into quadrant I of the Cartesian plane. Note that since you have shifted the position of the vertex, the parabola intercepts the y axis when y equals 19.
You achieve a different effect if you employ negative numbers to define the a and h constants of the quadratic equation. Consider the following equation:
–2[x – (–4)]2 + 3
This equation unfolds so that the coefficient or slope of x is negative. For this reason, the vertex of the parabola points downward. Since the value of h is negative (–4), you shift the vertex to the left of the y axis. While you make the first two constants negative, you set the value that corresponds k to 3. This action, as in the previous example, translates the vertex upward. As Figure 9.11 illustrates, the vertex of the parabola lies in quadrant II of the Cartesian plane. The maximum value lies at (–4, 3).
Figure 9.11. A negative slope and a negative shift value invert the parabola and move it to the left, but you still shift it upward 3 units.

The x-intercepts
The points at which the graph of the quadratic equation cross the x axis are known as the x-intercepts. If you can determine the vertex of the parabola, and know whether the parabola opens upward or downward, then you are in an excellent position to calculate the x-intercepts. As the previous examples reveal, not all quadratic equations have x-intercepts. For example, if a parabola opens upward and is shifted upward from the x axis, it does not intercept the x axis.
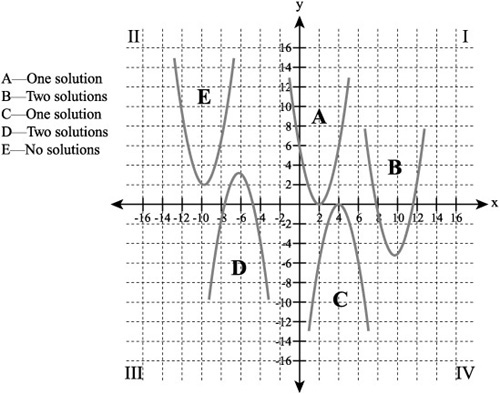
Figure 9.12 provides a summary view of a few possibilities with respect to quadratic equations. Accordingly, parabola A has one x-intercept because its vertex lies on the x axis. The same is true of parabola C. Parabolas B and D have two solutions each because they intersect the x axis in two places. Parabola E has no solutions because its origin lies above the x axis and it opens upward.
Figure 9.12. When you solve for the values of a quadratic equation, you determine if the parabola the equation generates intersects with the x axis.