The Distance Between Points
To take the preceding discussion a step further, consider once again the distance between two points on a line. In Figure 7.1, you establish a relationship between two ordered pairs, (4, 9) and (1, 5). As the figure reveals, the distance between the two points can be viewed in terms of the differences between the corresponding elements of the two ordered pairs. Accordingly, the difference between 9 and 5 is 4 and the difference between 4 and 1 is 3. The figure uses the delta character to show this difference (or change).
Figure 7.1. The change in the rise is 4 and the change in the run is 3.
Applying the Pythagorean Theorem
The two points in Figure 7.1 define two of three points in a triangle. The difference between the corresponding x values of the two points gives you the distance that defines the base of the triangle. The difference between the corresponding y values of the two points gives you the distance that defines one side of the triangle. Given the measurements of the base and a side of a triangle, you can then draw upon the Pythagorean theorem to find out more about the triangle.
According to the Pythagorean theorem, the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the remaining two sides. The theorem is usually expressed along the following lines:
c2 = a2 + b2
where c represents the hypotenuse and a and b represent the remaining two sides. If you know that one side of a triangle is equal to 2 and another is equal to 4, then proceed to solve the equation in this manner:
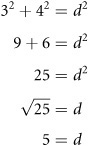
Exercise Set 7.2Using the Pythagorean theorem, use these values for the sides of triangles and calculate the length of the hypotenuse.
|
The Distance Formula
Given the grounding the previous section provides, you can set up an equation to calculate the distance between two points in this way:
Δx2 + Δy2 = d2
The d is the distance between the two points. From the perspective afforded by the Pythagorean theorem, the difference the delta sign signifies is the difference between the corresponding elements in the coordinate pairs you use in your calculations.
To return to the discussion of the point-slope equation, you can revise it slightly using what you know about the Pythagorean theorem. Consider a line on which you have identified two points, (x1, y1) and (x2, y2). Drawing upon the formulation of the Pythagorean theorem introduced in the previous section
Δx2 + Δy2 = d2
you can then proceed to establish a specific formula, called the distance formula, for determining the distance between two points:
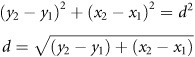
Having attended to these preliminaries, you can then ascertain the distance between any two points on a line in a fairly ready manner. Assume, for example, that you begin with two ordered pairs (2, −3) and (4, 7). You substitute these values into the primary terms of the equation:
Exercise Set 7.3Use these ordered pairs with the distance formula to find the distance between points.
|
Perpendicular Lines
Figure 7.2 provides an illustration of a basic linear function y = 3x + 2. The y-intercept is 2. The slope is 3. The line extends upward into quadrant I since the slope is positive. You see three coordinates on the line, the top of which is (2, 8). At the same time, the graph features a second line, one that slopes downward into quadrant IV. This second line runs perpendicular to the first line. It intersects the x axis at (6, 0).
Figure 7.2. The inverse creates a perpendicular line.
To create an equation that generates a line that is perpendicular to another line, consider in Figure 7.2 the equation that generates the line with the positive slope. The y-intercept is at (0, 2). The line slopes up into quadrant I. In addition to this line, you see another line. The second line has a negative slope. It slopes downward, into quadrant IV. It passes through the y-intercept (0, 2). Among the points in its path are (3, 1) and, as mentioned previously, (6, 0). The second line is perpendicular to the line with the positive slope.
To investigate the features of the perpendicular line, consider the expression you use to determine the slope of a line:
To make use of this expression, you can substitute the values given by the two ordered pairs as follows:
This gives you the slope of the second line 
, and given that you know the slope of the second line, you can then write the following slope-intercept equation:
You then have at hand an equation you can use to determine the point at which the line crosses the x axis. Toward this end, you can rewrite the equation so that you set y to 0 and solve for x:
To explore this notion from a slightly different perspective, here is an equation that provides the following negative slope:
As Figure 7.3 indicates, the y-intercept for this line is (0, 4). If you solve the equation for the point at which the line crosses the x axis, you arrive at (6, 0). If you set x to 3 for this equation, you find that the value of y is 2.
Figure 7.3. The multiplicative inverse of the slope allows you to generate a perpendicular line.
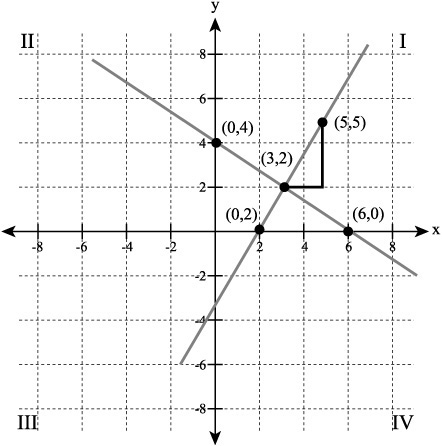
To create a perpendicular line beginning at the coordinate (3, 2), you can an add 2 to the run value and 3 to the rise value. In other words, you invert the values you obtain from the original slope, and then add them to the original slope. This gives you a point at (5, 5). Now you draw a line from the your initial set of coordinates to your new set of coordinates. You can then find a slope for the new line. You proceed along this path:
The multiplicative inverse of 
is 
. Your first slope was 
, however, so when you carry out the multiplication, you end up with −1.
Exercise Set 7.4Write the equations for the lines perpendicular to the given lines.
Determine whether each set of equations represents perpendicular lines.
|
