Inequalities
Figure 5.5 illustrates the four types of relations that describe inequalities. The relationships that characterize inequalities can unfold in inclusive and exclusive (or non-inclusive) ways. When you use a number line, representing inclusion or exclusion involves two basic activities:
A range of numbers can be greater than a given value on a number line. To show that the range of numbers is greater than a given number, you employ an open circle. The circle excludes the circled number from the range.
A range of numbers can be greater than or equal to a given value on a number line. To show that the number is included in the range, you use a filled circle.
Figure 5.5. Open circles exclude values while closed circles include them.
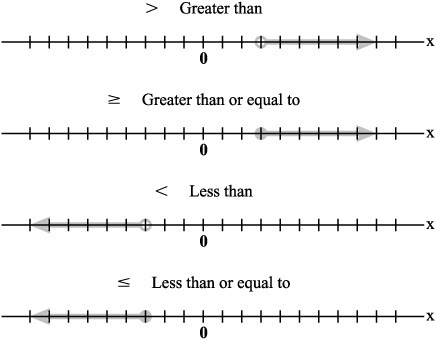
The same approaches apply to ranges of numbers that are less than or equal to a given value.
When you work with equations that deal with inequalities, you solve them in largely the same way you solve equations that involve equalities, but a few differences apply. Subsequent sections discuss these differences in detail.
Addition and Subtraction of Values
When you add values to both sides of an equation that involves inequalities, you do not alter the relation of the inequality between the two expressions. In other words, the relations
a < b and a ≤ b
remain the same if you extend them through addition:
a + c < b + c and a + c ≤ b + c
Likewise, the relations
a > b and a ≥ b
remain the same if you extend them through addition:
a + c > b + c and a + c ≥ b + c
Given that you can extend these relations to include the addition of additive inverses, you can safely add or subtract values to remove or isolate values on both sides of the inequality without changing the relation.
Here is an equation that involves inequalities and addition:
| x + 4 < 6 | |
| x + 4 – 4 < 6 – 4 | Undoing the addition of 4. |
| x < 2 |
You can represent this inequality by graphing it on a number line. The filled circle indicates that valid solutions are any numbers less than 2. In other words, 2 and any number greater than 2 are not members of the solution set.
![]()
As with equations involving relations of equality, you can substitute your solution into the original equation to test its validity. In this instance, the solution consists of a range of numbers less than 2, which you can designate as x |x < 2. This expression reads that the solution is any number x such that x is less than 2. Using this expression as a guide, you can arbitrarily designate the following set:
{–2, 0, 1, 1.5}
Given this set, you can substitute the solutions into the original equation:
(–2) + 4 < 6 = 2 < 6
(1.5) + 4 < 6 = 5.5 < 6
(0) + 4 < 6 = 4 < 6
(1) + 4 < 6 = 5 < 6
In each instance, the expression proves true, verifying the validity of your solution set.
Multiplication and Division of Values
Addition and subtraction of terms in an equation involving inequality renders no change in the relation of inequality. This situation changes with multiplication and division. Specifically, it changes in instances in which you multiply and divide by negative numbers. Why this is so relates the properties of real numbers. As was discussed in an earlier chapter, if you multiply a negative number by a negative number, a positive number results. Likewise, if you divide a negative number by a negative number, a positive number results:
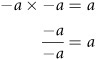
The effect of such activity is that when you work with an inequality, you must reverse the inequality sign if you divide or multiply a negative number by a negative number. Here is an example of how this happens:

When you divide by –4, the result of the division on the right side is a positive value, 1/2. This changes the inequality. You must reverse sign to compensate for this fact.
To test the validity of members of your solution set, substitute them into the original equation. You can graph the primary solution on a number line. The graphical representation shows that the solution is less than 1/2, so you use an open circle.
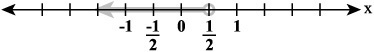
As an example of the effect of multiplying by a negative number, consider this inequality:

When you multiply by –1 to make the inequality easier to work with, you render the values on both sides of the inequality positive. This change makes it necessary to reverse the inequality sign.
As in the previous example, to verify the correctness of the solution set, you can first graph it on a number line.

To check the inequality, you can substitute the primary solution into the original inequality:
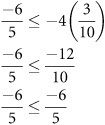
Exercise Set 5.6
|
