Long Division in Algebra

When you perform divisions involving polynomials, you use an approach similar to the one you employ for arithmetic. To perform such divisions, you group like terms and combine them. You also order the terms relative to their degree in descending order. Likewise, it is helpful if you remove fractions and in other respects simplify the expressions as much as possible before attempting the division.

As an example of a polynomial division problem, consider this expression:

The terms in the numerator appear in descending order with respect to the degrees of their exponents. In this case, the largest degree is that of the square of x. The same applies to the terms of the denominator, where the highest degree is 1.

To set up the division, you proceed in the same manner you did when you performed long division involving whole numbers:

To perform the division, you concentrate first on the term with the exponent of the highest degree. Carrying out such a division is analogous to long division in arithmetic. You can envision 8642 in this way:

8 · 10³ + 6 · 10² + 4 · 10¹ + 2 · 10⁰

In the previous section, for example, in essence you first divide 8 × 10³ by 41. Ten raised to the power of 3 constituted the highest degree of ten as given in the problem. Having dealt with the highest degree of 10, you then move on to the second highest degree.

In this instance, you concentrate first on the highest power of x, which is 2. Isolating the terms involved, the division takes this form:

You then multiply x + 3 by 2x to arrive at the expression you subtract from the dividend. The multiplication proceeds as follows:

2x (x + 3) = 2x² + 6x

Given this term, you then subtract the term from the dividend and find the remainder:

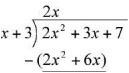
To carry out the subtraction, it is necessary to consider the signs of the terms in the subtracted expression. To prevent errors, you can treat the subtraction as an addition problem and change the signs of all terms in the subtracted expression:

You then carry out the next step, which involves dividing −3x + 7 by x + 3. To carry out this division, you again concentrate on x, this time with an exponent of 1:

When you perform the long division, you multiply x + 3 by −3, to obtain −3x − 9:

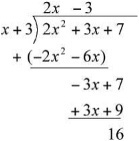
After you carry out the subtraction, the remainder in this instance is 16, so the answer is

Exercise Set 8.4 Solve each equation using long division. (2 x2 + 11x − 5)÷(x + 6) (a2 + 4a − 12)÷(x − 2) (y2 − 10y − 20)÷(y − 5) (3b2 − 2b − 13)÷(b − 2) (12a4 − 3a2)÷(a − 3)