Completing the Square
Working with the basic form of the quadratic equation the previous section afforded, you gain some sense of what it is to complete the square of an expression to solve a quadratic equation. For starters, recall that these two equations represent standard forms of polynomials that incorporate squares:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
Generally, completing the square begins with examining an equation to discover whether you can rewrite it in a way that allows you to make a perfect square on the left side of the equal sign. To understand how this works, consider the following equation:
a2 – 6a – 12 = 0
This is a standard quadratic equation. To make it so that it represents the square of two expressions, you begin by considering the first two terms. The first term is a square. The second term might represent the combined square roots of two squares. (The variable, a, for example, is the square root of a2.) The third term, however, does not easily fit into this scheme. For this reason, you move 12 to the right side of the equal sign:
a2 – 6a = 12
You then find a term that you can add to the left side of the equation that allows you to create a perfect square. To arrive at this number, you use an expression you derive from the standard form of the quadratic equation. Accordingly, the second term of the standard equation is bx. If you divide b, the coefficient of x, by 2 and square the result, then you arrive at an expression that completes the square. Here is how this approach unfolds for the equation at hand:
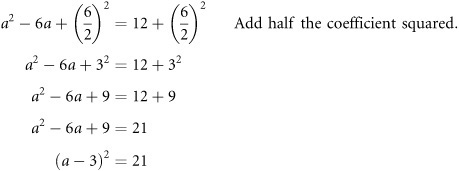
You can then solve the last form of the equation using the approaches rehearsed previously:

Since the value of a is greater than zero, two solutions exist. The solution set is as follows:
![]()
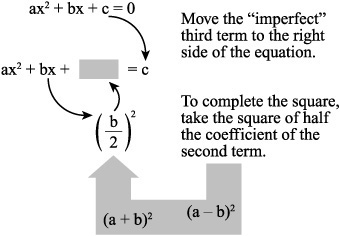
Figure 9.13 reviews the general technique you use to complete squares.
Figure 9.13. To complete the square, divide the coefficient of the second term by 2 and square the result.
In many instances, completing the square involves working with coefficients of the first term that are greater than 1. Consider, for example, the following equation:
2x2 – 3x – 1 = 0
In this instance, the coefficient of the first term is 2. To alter the equation so that you proceed as before with completing the square, you multiply the equation by the inverse of the coefficient. In this case, the inverse of 2 is ![]() , so your work takes the following form:
, so your work takes the following form:
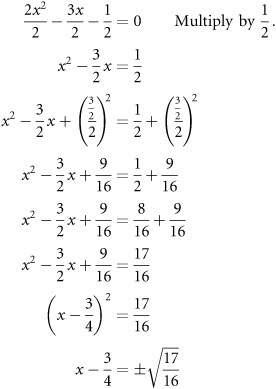
Having proceeded this far, you can then rationalize the denominator of the expression on the left side of the equation. This gives you
![]()
The solution set for the equation is as follows:
![]()
Exercise Set 9.1Solve by completing the square. |
