The Ratios of Trigonometry

A set of functions, known as the trigonometric functions, allow you to extend the work of algebra and geometry in several directions. To understand the trigonometric functions, you can start by examining the ratios that exist between the angles and sides of a right triangle. To explore how these ratios are related to the activities previous chapters discussed, you can begin with an examination of the right triangle and how it relates to a line you generate using a linear equation.

Angles and Sides

Two of the angles of a right triangle are acute angles. In other words, they are angles of less than 90°. One is usually labeled as angle A. The other is labeled as angle B. A third angle is equal to 90°. According to the standard way of depicting a right triangle, the 90° angle is labeled as C. Likewise, a small square tucked into the angle identifies angle C as a right angle (see Figure 12.1).

The line opposite angle A is line BC. It is called the opposite side. You can designate the length of this line using the letter a. The line opposite to angle B is called the adjacent side. It is adjacent to angle A. You can designate its length with the letter b.

Opposite the right angle is the hypotenuse of the triangle. This side of the right triangle is always the longest side of the triangle. You can refer to it geometrically as line AB. You can also designate the length of this side using the letter c.

The Pythagorean Theorem

Given the standard way of identifying a right triangle, you can then introduce the Pythagorean theorem as a way to relate the three sides of a right triangle. Here’ s the standard equation for the Pythagorean theorem:

c² = a² + b²

You rewrite this equation to eliminate the exponent of c :

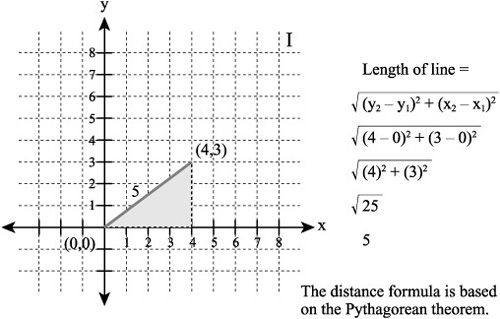
When you put the Pythagorean theorem to work in a Cartesian plane, you can see that the lines you create using linear equations can be mapped in a fairly direct way to a right triangle. As Figure 12.2 illustrates, if you regard the origin of the coordinate system as corresponding to angle A, then you can establish the rise and the run of the triangle as the opposite and adjacent sides. The adjacent side follows the x axis. The rise of the opposite side follows the y axis. You can regard the line itself as the hypotenuse. You use the Pythagorean theorem to determine the length of the line.

The position of the right triangle you create when you generate a figure using linear equations gives you a point of reference that centers on the origin of the Cartesian plane. For a triangle you depict the angle according to the standard model discussed in the previous section; this is angle A. A convenient way to label an angle is to use the Greek letter theta, θ. Accordingly, the angle of θ is always relative to the run and rise of the triangle.

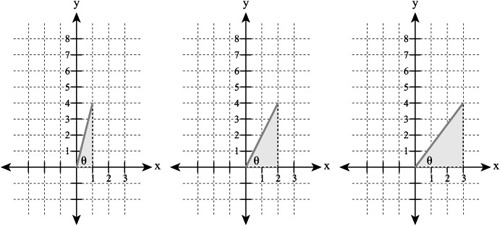
As Figure 12.3 illustrates, if you work within the first coordinate of the Cartesian plane, as the angle of θ increases, the slope of the line becomes more pronounced. The length of the opposite side increases. The length of the adjacent side decreases. As you saw when you investigated slopes, the ratio of the adjacent to the opposite side allows you to determine a value for θ.

Circles and the Sine of 2

You can transfer a right triangle you construct in a Cartesian coordinate system to a circle. When you translate the triangle to a circle, the center of focus remains on the angle that characterizes the origin (θ). As Figure 12.4 illustrates, the hypotenuse of the triangle provides a way to establish the radius of the circle. Along with the hypotenuse of the circle, you can also establish a chord on the circle. The chord in this instance is one that is twice the length of the opposite side. To create such a chord, you can flip the right triangle downward, from quadrant I into quadrant IV. You identify the chord by using the term 2θ.

If you take half the distance of the cord, you have a line that you define using θ alone. This line is known as the sine of θ. The sine of theta, then, corresponds to the ratio that you establish between the distance of the hypotenuse and the distance of the opposite side.

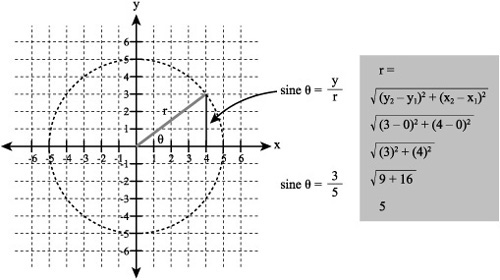
If you want to determine the sine of θ as shown in Figure 12.4, you can put to work the information the graph provides. Accordingly, if you work within quadrant I of the Cartesian plane, you can see that the coordinate pair that describes the point on the circumference of the circle for the line is (4,3).

To calculate the length of the line that extends from the center of the circle (or the origin of the Cartesian plane), you use the Pythagorean theorem. Following the generalization of the situation Figure 12.5 provides, you can see you can calculate the sine of θ using the data you possess with the point (4,3). First you calculate r, the hypotenuse. Then you find the ratio of y to r.