Number Systems

When you solve math problems, you work with different systems of numbers. The systems of numbers often allow you to express the same numbers differently. In your earlier studies of math, it is likely that you became familiar with some of the numbering systems. As you study more math, you work extensively with several systems of numbers. The next few sections discuss the different systems.

Natural or Counting Numbers

The natural or counting numbers start at 1 and proceed in increments of 1 indefinitely. You work with situations in which your activities may lead to an object or objects that you might point to, or count. For this reason, it is fairly easy to recognize that the natural numbers system probably constitutes the oldest way of counting things. You might imagine, for example, a potter working in a situation in which he or she makes a series of pots. To count the pots, it’s necessary only to line them up or draw lines in the earth. Consider Figure 2.1.

The mathematical symbol for natural numbers is N. Here is one way to mathematically describe natural numbers:

N = {1, 2, 3 ...}

The N preceding the equals sign indicates that all the numbers belong to the set of natural or counting numbers. The three periods trailing the 3 indicate that the numbers continue indefinitely. The curly braces that enclose the numbers indicate that they constitute a set of numbers. We read this as the natural numbers are the set of numbers 1, 2, 3, and so on. A set is a group or collection. In this light, then, all number systems consist of sets of numbers.

Whole Numbers Offer You Zero

The marks and pots you see in Figure 2.1 provide you with a way to depict things that you can point to. What happens when you encounter situations in which you want to explain that you do not have an item of a given type? Suppose that the potter makes five pots and then sells them all? Enter the concept of zero, which is a way of saying that you recognize the possibility of having something even though you do not, in fact, have something at hand to point to. In other words, you have none of the objects.

Figure 2.2 illustrates how the use of 0 in the whole numbers system proves to be a useful way of dealing with a complex notion. The whole numbers allow you to both point to something and point to the absence of something. As with the counting numbers, historians generally recognize the whole number system as being fairly old.

The mathematical symbol for whole numbers is W. As with the natural numbers, you can mathematically describe whole numbers as a set:

W = {0, 1, 2, 3 ...}

The W preceding the equals sign indicates that all the numbers belong to the set of whole numbers. The only difference between the natural numbers system and the whole numbers system is that the whole numbers system adds the use of 0. As before, the three periods trailing the 3 indicate that the numbers continue indefinitely. The curly braces that enclose the numbers indicate that they constitute a set of numbers. The natural numbers (N) are a subset of the whole numbers (W). That is, every natural number is also a whole number.

Integers Provide Negative Numbers

Given the notion that you can have items at hand or that you can think about items of a given type without having any at hand, it seems almost inevitable that you run into another situation. This situation is one in which you need an item of a given type that is not at hand. Consider, for example, a situation in which you have no pots at hand but five people approach you and ask for pots. You now need to make five pots. You express this situation using negative numbers, as Figure 2.3 illustrates.

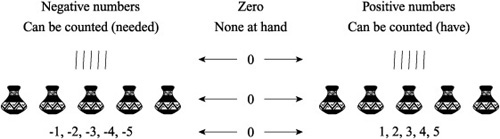
Integers include the positive numbers, zero, and the negative numbers. While the whole numbers start at 0 and proceed indefinitely in a positive way, the set of integers includes the whole numbers and proceed indefinitely in a negative way. You can think of 0 as a starting point between the positive and negative groups of numbers. The mathematical symbol for integers is Z. Here is how to mathematically represent the set of integers:

Z = {0, ±1, ±2, ±3, ±4, ±5...}

As with counting numbers and whole numbers, you see the curly braces, which represent a set. You also see a plus-or-minus sign preceding each of the numbers in the set. Use of the plus-or-minus sign serves as a way to shorten the mathematical expression from its longer form:

Z = {...−5,−4,−3,−2,−1, 0, +1, +2, +3, +4, +5...}

The second expression conveys the same information as the first, but in this case, a minus sign (−) precedes each negative number and a positive sign (+) precedes each positive number. Likewise, you see that ellipses precede and follow the numbers. Notice the zero possesses no sign. You can certainly apply a sign to a zero without doing any harm, but the fact remains that the sign has no effect on zero. Zero is neither negative nor positive.

When you use integers, you never need to indicate a positive value using a plus sign. As a matter of common practice, if you see a number standing alone without a sign, it is positive. Here is another way to show the longer form of the set of integers:

Z = {...−5,−4,−3,−2,−1, 0, 1, 2, 3, 4, 5 ...}

So far you have looked at natural numbers, whole numbers, and integers. The relationship between these number systems is as follows: Every natural number and every whole number is a number in the set of integers. In other words, W is a subset of Z and N is a subset of Z. Also, recall that N is a subset of W.

Rational Numbers

Even if you can count things at hand, recognize things when they are entirely absent, or count them in a negative or absent form, you still face situations in which you need to account for things that are not quite whole. To deal with this situation, one approach involves working with the concept that you can establish a ratio between two numbers.

As Figure 2.4 illustrates, picture the situation of a potter whom customers have asked to make five pots. The potter has made three pots. A customer arrives and requests to know how much of the work of making the pots has been completed. The potter can reply by asking the customer to imagine the whole set of five pots and then another set of three pots. Of the five needed pots, the potter has finished three. So the reply of the question can be, “The number is 3 of 5.” This expresses a ratio.

A rational number is a number you use to express a ratio or relationship between two other numbers. You can communicate a ratio by creating a quotient. A quotient is a result you obtain when you perform a division.

Consider the ratio of 3 to 5. In simple terms, you divide 3 by 5. Here are a couple of common ways to express this activity mathematically:

The mathematical symbol for rational numbers is Q. Here is how to mathematically represent the set of rational numbers:

The vertical bar means “such that,” and the means “is a member of.” The hashed equal sign means “not equal to.” The definition reads, “A rational number (Q) is any number p/q, such that p and q are elements of the set of integers (Z) and q is not equal to 0.”

Here is a set of rational numbers:

{−1/5,−3/4,−2/3,−1/2,−1/6, 0, 6/7, 4/2, 21}

Notice that the elements in this set are negative, include zero, and positive. Also note that 0 and 21 can be expressed as ratios: 0/0 and 21/1.

No Division by Zero

When you formally define a rational number, the two numbers you include in the quotient, p and q, are both integers. The lower number, q, cannot be equal to 0. You cannot divide by 0.

We know that because 2 × 3 = 6. If we consider , the answer must be a number that, when multiplied by zero, results in 6 (i.e., = x where x × 0 = 6), but x × 0 = 0 for all x’s. Therefore, has no value. Mathematicians say that such a relation where any number is divided by zero is undefined.

Staying Clear on Your Numbers Just because you can represent a number as a quotient does not mean that it is only a rational number. The fact is that you can represent counting numbers, whole numbers, integers, and rational numbers as quotients. Consider the following representations of numbers: All of the representations denote 2, which is a counting number, a whole number, an integer, and a rational number. When the quotient provides a “rational” way to represent the number, whether in its quotient or non-quotient form, the number remains a rational number. The representations of −2 on each side of the equal sign designate integers. The number −2 can be represented as ,,, or . Therefore, it is a rational number as well as an integer.

Variations on Rational Numbers

When you carry out division, you end up with different types of quotients. To repeat, a rational number is a number that you can express as a ratio. You can express an integer as a ratio, as you can a whole number. In some cases, you can reduce the quotient form of the number to a whole number. In other cases, the quotient form of the number cannot be reduced to a whole number, and therefore has a decimal representation. A number is rational if its decimal representation is terminating or repeating.

Terminating Rational Numbers

If the decimal representation of the quotient can be expressed by an exact number of digits, then it is a terminating rational number. Consider the following numbers and their decimal representations:

In each case, the result of the division is exact. A melon can be divided into two equal parts. It can also be divided into equal fourths. Likewise, you can have exactly three fourths of a melon, as you can have five sixths of a melon.

Repeating Rational Numbers

In some cases, when you establish a ratio between two numbers, the quotient is not terminating. You do not end up with exact pieces or proportions (i.e., the decimal representation does not have an exact number of digits). The most you can do is approximate the piece or proportion. Consider, for example, what happens when you divide 1 by 3 or 2 by 3. The result is a repeating rational number:

1/3 = 0.3333333333 ... and 2/3 = 0.6666666666 ...

Mathematicians indicate the repeating part of the fraction by placing a bar above the number that repeats:

When a single number repeats, you need only one number bearing a bar. In other cases, the pattern of repetition involves several numbers. In that case, you use the bar to designate the sequence of numbers that repeat. Consider the pattern that results when you divide 1 by 7 and 1 by 17:

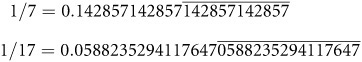
Whether you encounter a single repeating number or, as in the case of 1/17, groups of 16 repeating numbers, you are still working with a number that you can represent explicitly. You can show that at a given point, the number begins to repeat itself. You need not show the repeating decimals more than once. For example, you can also represent the numbers this way:

Irrational Numbers

When you perform some divisions, the number you end up with is neither exact nor repeating. Consider, for example, the ratio of the length of the circumference of a circle to the length of its diameter. The ancient Greek letter mathematicians use to designate this ratio is π (pi). When you try to find a terminating or repeating rational number to designate π, you fail. The quotient you generate is not exact, and it does not repeat itself at periodic intervals. Here is a sampling of the number that results:

3.141592653589793238462643383279502884197169399375 ...

At this point in history, π has been calculated to billions of digits. No repeating set of numbers has turned up. Such a number is known as an irrational number. The mathematical symbol for an irrational number is H. Here is how to mathematically represent the set of rational numbers:

H = {x | x R x Q}

Again, the vertical bar means “such that” and the means “is a member of.” The R designates the set of real numbers (discussed below), and the means “is not a member of.” The definition reads, “An irrational number (H) is any number x, such that x is an element in the set of real numbers and is not in the set of rational numbers.”

Some other numbers that fall into the irrational category are the square root of , the cube root of , and the base of the natural logarithm, e (log_ex). A number is irrational if its decimal representation is non-terminating and non-repeating.

Real Numbers

All of the numbers you have investigated so far are considered real numbers. The mathematical symbol that represents real numbers is R. Figure 2.5 reveals the relationship between the various number systems. Accordingly, both rational and irrational numbers are real numbers.

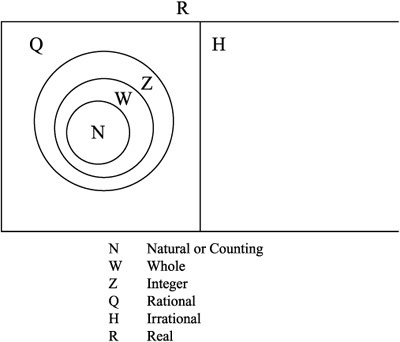
It remains important to emphasize that a number may be represented in many number systems. For example, a rational number may also be a counting number, a whole number, or an integer.

Exercise Set 2.1 To test your understanding of the systems of numbers, please identify the number set the following numbers belong in. Identify the innermost set for each number. Example: 4/2 N π −2 −6/3 −5/2 −2/3 4/5 2/1 1/8 1/5