Translation Along the x and y Axes
When you graph a quadratic equation, in many instances, you find that the vertex of the parabola you generate corresponds to the origin of the Cartesian plane (0, 0). The discussions of linear equations in Chapter 7 and elsewhere emphasize that while many linear equations cross or intersect with the origin of the Cartesian plane, by shifting an intercept value, you can raise or lower the intercept point. The same situation arises when you work with quadratic equations.
When you consider the coordinate pair that defines the vertex of a parabola, you deal with the minimum value of the parabola if it opens upward. You deal with the maximum value of the parabola if it opens downward. You can shift this value so that it moves along the x axis or along the y axis. If you move it along the x axis, you translate it horizontally. If you move it along the y axis, you translate it vertically. You translate the vertex in a positive fashion if you shift it up or to the right. You translate the vertex in a negative fashion if you translate it downward or to the left.
To understand the mechanics of translating the vertex of a parabola along the x axis, consider an expression of the following form:
ax2
You can rewrite this expression so that you replace the variable x with a different expression. The new expression allows you to view x as the difference or sum of two other values. Accordingly, you might rewrite the expression in this way:
a(x – h)2 Replacing x with x – h
You now have a situation in which you are dealing with the square of the difference of two terms. In this case, h designates a value you can use to translate the vertex of a parabola along the x axis.
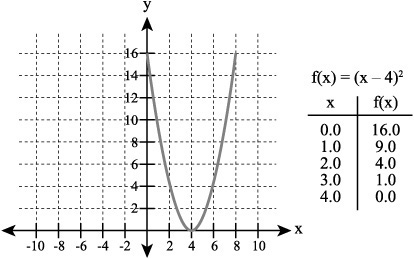
Translating to the Right
As Figure 9.7 shows, when h is a positive number, then the translation is to the right. On the left of the figure, the value of h is set to 0, so no shift occurs. On the right, the value is set to 4, so the shift is four units to the right. As you can see from the figure, if the equation is of the form a(x – h)2, and the constant a is a positive number, the vertex of the parabola opens upward. The position of the vertex is defined by the ordered pair (h, 0). Given this position on the x axis, you can locate the line of symmetry at the position on the x axis that corresponds to the value of h. Since a has a positive value, the vertex of the parabola opens up, so the minimum value of the parabola is 0.
Figure 9.7. A positive value creates a difference of two terms and shifts the vertex to the right.
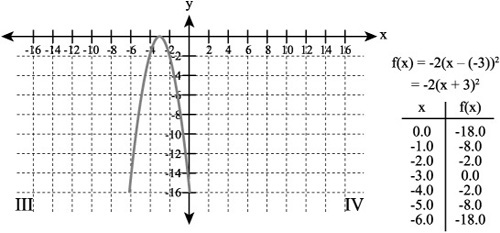
Translating to the Left
If you again rewrite the expression ax2 so that x can be defined by the difference of two values, you arrive at an expression that reads a(x – h)2. If you then substitute a negative value for h, you end up with an expression that appears as a(x –(–h))2. Figure 9.8 illustrates a situation in which you use a negative value in a quadratic equation in this way. The basic effect of this operation is the same as if you carried out an addition of the form (x + h)2. The result in the graph is that the vertex of the parabola is shifted to the left of the origin on the x axis by 4 units.
Figure 9.8. A negative value creates a difference of two terms and shifts the vertex to the left.
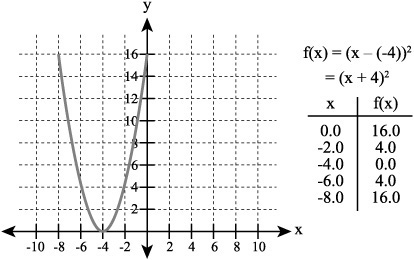
As with the previous example, the position of the vertex is defined by a coordinate pair in which the value of the first coordinate is 0. In this instance, the value of the second coordinate is a negative number (0,–4). The location of the line of symmetry on the x axis is the value of–4. As in the previous example, since the value of a is positive, the parabola opens upward.
Inverting and Translating
As you might expect, no restriction prevents you from both inverting and translating a parabola. To accomplish this, you set the slope value (a) to a negative number. As in the previous sections, you can also continue to substitute the expression x – h for x to shift the vertex along the x axis. For example, if you set h to –2, you invert the parabola, and if you set a to –3, you shift it to the right. You arrive at a parabola similar to the one Figure 9.9 illustrates.
In Figure 9.9, since the value of a is a negative value (–3), the parabola has a negative slope. The coordinates defining the vertex are (0, –3), so –3 is the line of symmetry.