Absolute Values

Consider what happens when you provide someone with directions to a given destination. You might receive instructions that indicate distances without necessarily providing you with the direction in which you are traveling. Consider, for example, an instruction that reads,

“After you turn onto Highway 36, proceed 7 miles.”

Given this instruction, Figure 3.2 illustrates two scenarios. Starting at a given point, you can then proceed in one of two directions. The distance you travel involves real movement regardless of whether it takes you nearer to or farther from your destination. The distance you travel, then, has an absolute value.

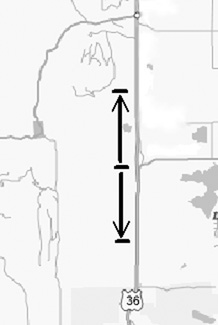
Absolute value is the value of a number without respect to whether it is positive or negative. A number line provides a convenient way to illustrate an absolute value. Figure 3.3 illustrates a number line. You can use a number line to represent the arrows depicted in Figure 3.2 in numerical terms. Given this vision, the number line translates the absolute values of the two directions Figure 3.2 depicts. The number line depicts the distances from 0 to 7 and from 0 to -7. In both cases, the absolute value is 7.

Figure 3.3. The number line depicts the absolute value.

[View full size image]

To express mathematically the absolute values of positive and negative numbers, you enclose the number in vertical bars.

| –7 | = 7

| 7 | = 7

The absolute value of a positive number is the number itself. The absolute value of a negative number is the additive inverse of the number. Consider the following operations with respect to absolute values:

| – 7 × 3 | = | – 7 | × | 3 | = 7 × 3 = 21