Exponents
When you multiply a number by itself, you raise it to a power. A power is a product in which all of the factors are the same. To indicate that you are raising a number to a given power, you employ an exponent. An exponent tells you the number of times by which you multiply a number by itself to arrive at the value you seek. Consider the following expressions:
| a × a = a2 | 2 × 2 = 22 = 4 |
| a × a × a = a3 | 2 × 2 × 2 = 23 = 8 |
| a × a × a × a = a4 | 2 × 2 × 2 × 2 = 24 = 16 |
In the expression a2, the a is the base of the expression, and the 2 is the exponent. The base provides the number you use in the multiplication. The exponent tells you how many times to multiply the number by itself.
Negative Numbers with Powers
When you use a negative number as an exponent, you create the inverse of the power. Consider the following expressions:
In each instance, the negative exponent signals that you are dealing with the inverse of the number. This holds true for all numbers not equal to zero and all exponents greater than zero. A number multiplied by its inverse equals 1.
Multiplication
If you are working with base numbers that are the same, then you can add the exponents of the numbers to multiply the numbers. Consider the following expression with relation to multiplication:
am × an = am+n
22 × 24 = 22+4 = 26 = 64
Both of the terms provide 2 as a base. Given this situation, as long as you express the numbers you are working with using the same base terms, you can add the exponents to carry out the multiplication.
What if the bases are not the same? If you start with numbers that differ, you can in many cases change them so that they represent the same base. Consider this example:
22 × 42 = 22 × 24 = 22+4 = 26 = 64
In the first expression, the bases 2 and 4 are not the same. However, 4 = 22 and 42 = 22 × 22 = 22+2 = 24. By manipulating the base, you can create an expression that allows you to add the exponents to carry out the multiplication.
Division
If you are working with the same base number and you divide one base number by the other, then you can subtract one exponent from the other. Consider the following:
am ÷ an = am-n
24 ÷ 22 = 24-2 = 22 = 4
Alternatively, to test the relationship, do the multiplication for each term:
24 ÷ 22 = 16 ÷ 4 = 4
When you multiply a number that has a positive exponent by a number that has a negative exponent, you create a situation characterized by division. Here is such a situation:
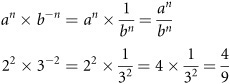
In this instance, in the lower example, the negative exponent turns 3 into 
. At the same time, 3 is still raised to the power of 2, so you see 
or 
. The first term, 2, possesses a positive exponent, and 22 = 4.
Division with a Negative Exponent
Consider likewise the effect of dividing a number by a number that possesses a negative exponent:
Dividing 43 by 4–4 is the same as multiplying 43 by 44.
Negative Numbers and Exponents
When you raise a negative number to a given power, whether you raise it an even or odd number of times makes a difference. If you raise a negative number by an even power, then you multiply it by itself an even number of times, so the result is positive. If you raise a negative number by an odd power, then you multiply the number by itself an odd number of times, so the result is negative. Consider the following expressions:
| (–3)2 = (–3) × (–3) = 9 | Even number power is positive. |
| (–3)3 = (–3) × (–3) × (–3) = –27 | Odd number power is negative. |
| (–3)4 = (–3) × (–3) × (–3) × (–3) = 81 | Even number power is positive. |
Powers of Powers
You can raise a power by a power. In this case, you multiply one exponent by another. Here is an example:
(22)3 = 22×3 = 26 = 64
(52)2 = 52×2 = 54 = 625
Powers of Zero and One
A number that possesses an exponent of 1 is equal to itself:
a1 = a 31 = 3
A number raised to the power of zero is equal to 1:
a0 = 1 30 = 1
Worked Problems with Exponents
Here are a few worked problems. Study them to prepare yourself for the next section.
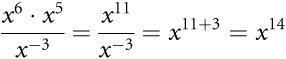
In this example, you face the problem of first adding the exponents on the top of the fraction. Then, on the bottom, you have a negative exponent, so you divide by 
which is the same as multiplying by x3.
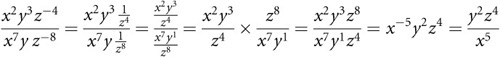
The key here lies in recognizing the need to deal with the two negative exponents. After you have created fractions that remove the negative signs, you can then carry out the divisions. You invert the bottom fraction, placing z8 on the top of the fraction. In the end, to remove the negative exponent from the top (x–5), you end up with a fraction.
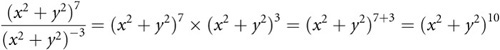
This problem presents difficulties because it anticipates work with polynomials, which receives attention in the next chapter. You cannot reduce an expression like (x2 + y2) without factoring it, so to work with it in this context, you treat it as a single term.
Exercise Set 3.1Simplify these problems involving exponents: |
Things That Go Wrong
Simple uses of exponents sometimes create situations in which it is easy to make mistakes. To investigate how this happens, begin by considering the following situation, in which you are dealing with a sum enclosed in parentheses and then raised by the power of 3:
(2 + 3)3 = 53 = 125
This solution for the problem is correct. You carry it out by first resolving the addition enclosed in the parentheses. The result of the addition is 5. You then raise 5 to the power of 3, which results in 125.
Here are a couple of other such problems, each solved correctly:
(2 + 5)2 + (2 + 4)2 = 49 + 36 = 85
(22 + 4)2 +(4 + 2)2 = (4 + 4)2 +(6)2 = 82 + 62 = 64 + 36 = 100
With both of these problems, you first attend to the operations enclosed in the parentheses before dealing with the exponents that apply to the value within the parentheses.
Things go wrong, however, if you inappropriately apply the distributive property to such operations. Here is the wrong approach to solving a problem:
| (2 + 3)3 = 23 + 33 = 8 + 27 = 35 | Not correct |
This is not the correct approach to solving problems because you cannot distribute the operation of the exponent across the two values in the parentheses. The parentheses make (2 + 3) into one expression. You must add these values before you move on to working with the power of 3.
Here is another way you can represent the problem:
(2 + 3)3 = (2 + 3)(2 + 3)(2 + 3) = 5 × 5 × 5 = 125
In this representation of the problem, the expression in the parentheses is multiplied by itself three times. This is what the power 3 instructs you to do. It applies to the whole expression, not to the values in the parentheses separately.