Thinking About Equations
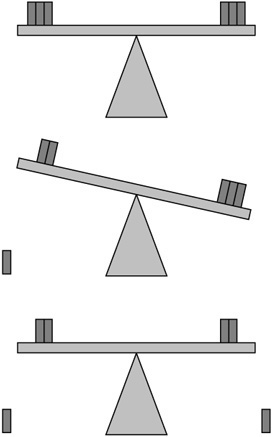
When you equate one thing to another, you usually proceed such that you examine two things in succession and then conclude they represent the same thing. When you look at a picture of a bird in flight and think about being free to sing, dance, or write a poem, you deal with an analogical form of equality. As Figure 5.1 illustrates, you can analogically equate an oval and a circle. The two forms are rounded, for example, or of the same shade. To the idea of analogy, you can also add that of balance. You can balance a single block on a scale with three smaller blocks if the combined weights of the three smaller blocks equal that of the larger block. With both analogy and balance, you establish equality by using a given quality or attribute to relate two or more items to each other.
Figure 5.1. Analogy and balance provide two ways to examine equality.

When you equate two things to each other, you can do so because they possess a quality or qualities in common. Mathematicians assert generally that everything in the universe can be related to everything else using numbers. Numbers provide a universal medium of relation.
When you study math, it sometimes becomes easy to forget that numbers are abstractions of things. For example, you see an expression along the following lines:
7 = 2 + 4 + 1
This is a relationship of equality between numbers that might stand for other things, such as the weights of blocks or days of the week. Reasserting that numbers represent such things becomes important at times.
As Figure 5.2 illustrates, when you deal with equations, you deal with both analogy and balance, but in many ways the notion of a balance proves most effective as a way of understanding how equations work. Working with an equation is a process of balancing. When you relate numbers to each other using an equation, you make it so that you can change the way you represent numbers. As you change the way you represent the numbers, you can solve the equation for specific values.
Figure 5.2. Working with an equation involves maintaining a balance.
An equation, then, consists of a relation you establish between numbers. When you establish the relation, you assert that a balance or condition exists between the representations you provide of the numbers.
You balance equations by manipulating their terms. As the discussion in Chapter 2 emphasized, you manipulate the terms of an equation using the properties of addition, subtraction, multiplication, and division. When you manipulate the terms and expressions of an equation, the goal of your activity is to preserve the equality of the terms.
Addition and Subtraction
Solving equations using addition and subtraction provides what proves to be the easiest approach to viewing how equations work. Here’s an equation:
x + 3 = 7
This equation involves one unknown term (x). If you solve the equation, you find the value of the unknown term. To find this value, you can subtract 3 from both sides of the equation:
x + 3 – 3 = 7 – 3
x + 0 = 4
x = 4
As you carry out the operation, you preserve the equality. In the end, you eliminate enough terms from the equation to find the lone value of x.
Subtraction constitutes a form of addition (adding the inverse). You can begin with an equation of a slightly different form:
x – 3 = 7
x – 3 + 3 = 7 + 3
x = 10
In this instance, the actions you take amount to undoing or reversing the actions you take when you perform the subtraction. Still, by adding the same value to both sides, you eliminate terms to the point that you are left with only x and its value.
With both forms of the equation, when you substitute your final answer back into the original equation, you can check your solution. Here is the equation involving addition:
x + 3 = 7
(4) + 3 = 7
7 = 7
Here is the equation involving subtraction:
x – 3 = 7
(10) – 3 = 7
7 = 7
Exercise Set 5.1
|
Multiplication and Division
When you work with multiplication and division to solve equations, your actions proceed along lines similar to those you use when you work with addition and subtraction. Because division often involves work with fractions, however, your activities take on greater complexity. Still, the essential work of maintaining equality between expressions remains the same. Here is an equation you solve using division:
2x = 10
To or undo the relationship between 2 and x, you divide the expression by 2. When you divide by 2, you employ the multiplicative inverse of 2. The effect of this activity is to transform the coefficient of x into 1 while dividing 10 in a way that equates with this action. Here is how you proceed:

The multiplication brings about a division of 10 by 2. At the same time, it isolates x.
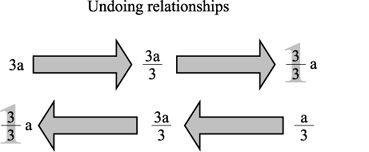
When you undo a relation between two terms, you are able to isolate one of the terms to discover its value. As Figure 5.3 illustrates, as long as the operations you perform on both sides of the equation result in equal changes, you can proceed with such activities until you reach the solution of the equation.
Figure 5.3. Equations allow you to do and undo operations.
What applies to division also applies to multiplication. Here is an equation that begins with a division:
![]()
Solving this equation involves undoing the division that characterizes the value of x. To undo the division, you can multiply by a value that results in 1x. Accordingly, you can multiply by 3:

As you proceed, then, you preserve the equality of the terms on both sides of the equation and isolate the unknown term on the one side so that in the end you can identify its value on the other side.
As with addition and subtraction, you can check your division and multiplication activities by substituting the values you arrive at back into the original equations. Accordingly, for the equation you solve using division:
| 2x = 10 | The original equation. |
| 2(5) = 10 | Substituting the solution. |
| 5 = 5 |
Likewise, for the equation you solve using multiplication:

Exercise Set 5.2 |
Combining Operations
Your ability to solve equations substantially increases when you combine addition and multiplication. With the combination of operations, you can proceed to undo relations that have bound numbers to each other in several ways. Here is an equation that combines numbers through addition and multiplication. You use division and subtraction to undo the relations. You begin by working with the addition:

When you work with an expression such as 2x + 3, to solve for x you begin by removing the integer 3 from the left side of the equation. You then remove the coefficient of x, 2. To remove the 3 from the right side, you subtract it from both sides of the equation. To remove the coefficient of x, you divide both sides by 2.
Along a slightly different path, consider the same equation you just worked with. There is more than one way to solve it. Instead of starting by undoing the addition, you can start by undoing the multiplication. In this case, you can begin by dividing. You start off by dividing both sides of the equation by 2:

When you divide by 2, you end up with fractions. The fraction associated with the unknown, x, however, is 2/2, which is equal to 1. In this way, then, you isolate the variable x. You can then use subtraction to deal with the fraction that remains on the left side. To verify that the solution you reached is correct, you insert it into the original equation:
2x + 3 = 7
2(2)+ 3 = 7
4 + 3 = 7
7 = 7
Approaching Equations in Different Ways
The previous section reveals that you can approach solving equations in different ways. The specific approach you use can be a matter of figuring out the approach you find easiest. Consider, for example, this approach to solving the problem presented previously:
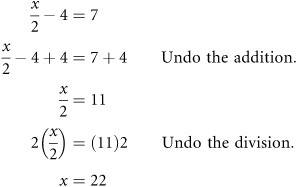
In this case, multiply by 2 to remove the fraction. When you remove the fraction, at the same time you first add 4 to both sides, and then multiply both sides by 2. You might just as well have started out by multiplying both sides by 2 but by first adding 4 you reduce the amount of work. To check the solution, you substitute it into the original equation:
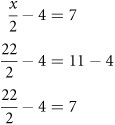
Here is another problem that involves multiple stages of undoing before you reach a solution. When you start off, the denominator of the fraction on the left consists of added terms. The most direct approach to dealing with this situation involves multiplying both sides right off by 7:

To check this solution, you substitute it back into the original equation:

Exercise Set 5.3 |
Least Common Denominators and Clearing Fractions
In the previous section, you multiplied by given values (such as 7) to get rid fractions. This activity is known generally as clearing an equation of fractions. To clear a fraction in an efficient way, you often make use of least common denominators. The least common denominator (LCD) is the number you get if you multiply together the denominators of the terms of the equation.
The least common denominator allows you to evaluate the terms of an equation according to a common denominator value. From there, you can then proceed to cancel terms. Here is an equation worked with on this basis:

With this equation, you multiply by 21, which you arrive at using the common multiples of 3 and 7. This is the least common denominator. After multiplying the terms of the equation by 21, you cancel terms and reduce the fractions. By first carrying out the work involving the fractions, you can more easily attend to the operations related to addition and multiplication.
Once again, when you substitute the solution back into the original equation, you can test the solution for validity. In this case, you also work with the least common denominator to reduce the resulting fraction to its most simple form:

As has been discussed previously, with many equations you make your work easier if you perform some preliminary activities involving addition or subtraction. Here’s an example of a problem in which you start off by reversing an addition operation and then moving on to clear a fraction and solve for x:

Substituting the solution back into the original equation allows you test the validity of your solution:

Here is one final example. You begin by clearing the fraction on the right side of the equation. To accomplish this, you multiply both sides of the equation by the value 6. This is a value you find in the denominator on the right side of the equation. Having cleared the right side of the equation, you can then more easily work to isolate the variable on the left side of the equation.

As with the previous examples, you can now substitute the solution back into the original equation to test its validity.

Exercise Set 5.4 |
