Extraction of Effective Cement Paste Diffusivities from X-ray Microtomography Scans
ABSTRACT. The problem of extracting effective diffusivities of cement pastes on the basis of X-ray microtomography images is considered. A general computational homogenization framework has previously been developed and is here applied to a variety of cement paste whose microstructure has been digitized to a resolution of 1 µm. With this resolution, important sub-micron features are not resolved. Consequently, we propose a methodology whereby the pore space is ascribed a diffusivity less than the free diffusivity. For this purpose a simple rule that incorporates microtomography data is proposed and shown to yield satisfactory results.
KEYWORDS: X-ray microtomography, cement paste, homogenization, numerical methods.
1. Introduction
The transport properties of cement pastes are of crucial importance to the durability of much of our civil infrastructure. Due to its corrosive effects and abundance in many natural environments, considerable efforts have been made to quantify particularly the transport of chloride. To date, most research has been concerned with the diffusive transport through fully saturated cement pastes and a number of specialized testing methods for evaluating the effective diffusivity have been developed (Tang and Nilsson 1992; Friedman et al., 2004; Krabbenhoft and Krabbenhoft 2008).
As an alternative to traditional experimental determination of transport properties of porous materials, a number of studies have recently demonstrated the feasibility of ‘virtual experiments’. The basic idea is here to obtain detailed three-dimensional images of the microstructure of the material after which the relevant tests are simulated and the quantities of interest, for example effective diffusion coefficients, are extracted in much the same way as in traditional physical laboratory tests. For the former task, X-ray microtomography (XMT) is typically used while the latter is carried out using either finite element/difference analyses or more specialized techniques such as lattice-Boltzman methods and Brownian motion simulations. Representative works combining both elements, i.e. imaging and simulation, include (Bentz et al., 2000; Knackstedt et al., 2006; Krabbenhoft et al., 2008; Promentilla et al., 2009).
Although the methodology described above is conceptually simple, it does involve a number of significant challenges. Firstly, one has to deal with very large data sets. Thus, digitized material elements consisting of more than one billion voxels (‘volume pixels’) is not uncommon. Regardless of which method of simulation is chosen, it is necessary to pay particular attention to this reality. In the present study where the finite element method is used, specialized iterative solvers for solution of systems of linear equations, which at times are severely ill-conditioned, have been developed. Furthermore, in order to limit the size of the problems solved in the actual simulations, a statistical homogenization procedure has been formulated. The resulting theoretical and computational framework is generally applicable to mass diffusion (as well as heat conduction and related physical phenomena) in porous and other heterogeneous materials.
Another, and in many ways more serious, complication with the virtual testing methodology, is that important microstructural characteristics may remain unresolved in the XMT scans. In the present study where XMT images of cement pastes at a resolution of approximately 1 µm are used, this is very much the case. As will be discussed in detail later on, this level of resolution does not account for submicron features that are of crucial importance to mass diffusion processes. Consequently, it is necessary to make a less sharp distinction between the solid and pore phases than would ideally be desirable. More concretely, we find it necessary to ascribe part of pore space a microscopic diffusion coefficient less than the free diffusion coefficient which would normally be expected to characterize the transport within the individual pores. A new rule that incorporates XMT data has been developed for this purpose.
The approach of not distinguishing sharply between the pore and solid phases has a number of similarities with other recent work, in particular that of Bentz (2000) who obtained microtomographic images of Fontainebleau sandstone and determined effective diffusivities numerically by means of a finite difference method. However, owing to the resolution of the images (19 µm, enhanced to 6.65 µm by optical magnification), the ‘solid phase’ was not considered impermeable but ascribed a not insignificant microscopic diffusivity. Furthermore, recent work of Promentilla et al. (2008, 2009) on cement pastes scanned at a resolution of 0.5 µm show that it generally is non-trivial to segment the raw grayscale XMT data into solid and pore phases. Moreover, it is demonstrated that the end result, in terms of effective diffusivity, depends strongly on the particular way that the segmentation is carried out. These findings are confirmed by the present study where the NIST Visisble Cement Data Set (Bentz et al., 2000) is used.
2. Numerical results
In the following, the results of diffusion through the pore space of the cement paste are presented. For the present study, the NIST Visible Cement Data Set (Bentz et al., 2000) was used. This data set contains images of cement pastes with difference water/cement ratios and at various stages of hydration. To illustrate the procedures developed, we will in the following use a particular data set which describes the microstructure of a cement paste with an initial water/cement ratio of ω/c = 0.45 and a hydration time of 137 hours.
Applying the computational homogenization procedure described by Krabbenhoft et al. (2008) and Karim and Krabbenhoft (2009), the diffusivities shown in Figure 1 are obtained. Also shown are the standard deviations. For each computed diffusivity
Figure 1. Computed apparent diffusivities: stochastic averages (left) and standard deviations (right). The number of voxels (and hence finite elements) in each RVE is given by δ3. The slight anisotropy between the x, y, and z directions is most likely a result of the preparation procedure (Karim and Krabbenhoft 2009).
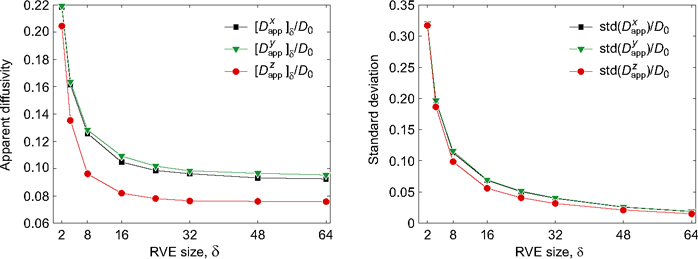
a total of 10,000 tests were performed. The diffusivity of the pore space was set equal to D0 = 1 while the diffusivity of the solid phase was set equal 10−10.
The cement samples scanned were in the form of cylinders with z denoting the longitudinal direction and x and y denoting to arbitrary directions in the cross section of the cylinder.
As seen, the computed mean values appear to attain near-asymptotic values at around δ = 30 while the standard deviation continues to decrease, though at a decreasing rate, as δ increases. The asymptotic values of the effective diffusion coefficients are:
(1) 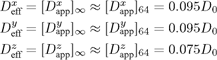
Concerning the absolute magnitude of diffusivities, Garboczi and Bentz (1992) have proposed the following expression:
(2) ![]()
where H is the Heaviside function. This formula is based on microstructural considerations and has been calibrated against experiments. By direct comparison to the above formula, we see that the computed effective diffusivities significantly overestimate what can be expected for a cement paste of the type considered. Indeed, for a cement paste with a porosity of around 29%, we should expect a value of Deff/D0 ≈ 0.028, which is a factor of three to four less than obtained in the present study. The possible reasons for this deviation will be discussed in the next section.
3. Correction for unresolved submicron features
The most immediate explanation to the deviation between computed and experimentally determined effective diffusivities is that the threshold level, Tps = 42, is too high. This threshold level was chosen on the basis of achieving a porosity of approximately 29%. However, in principle, a small change in threshold level could reduce the effective diffusivity significantly without altering the porosity correspondingly. If, for example, the chosen threshold is close to the percolation threshold, a small change in T would imply a potentially very large change in the effective diffusivity without affecting the porosity significantly. However, from Figure 2 we see that this scenario is not responsible for the deviation between computed and experimental determined diffusivities. Thus, in order to achieve an effective diffusivity of Deff/D0 ≈ 0.028, the threshold would have to be reduced to a level corresponding to less than 20% porosity, which for the given water/cement ratio is unacceptably low. We also see that the percolation threshold corresponds to a porosity of approximately 10% while (2) operates with a percolation threshold of 10%.
Figure 2. Effect of thresholding on porosity and computed effective diffusivities.

The second hypothesis is based on the observation that of the total pore space, constituting 28.8% of the volume, only 6.7% is recognized as a having a gray scale value of 0. The remaining 22.1% is attributed voxels with a grayscale value of up to 42. This obviously poses the question as to how representative the final digitized volume really is. In particular, it is somewhat worrying that a very considerable part of the pore space is not immediately recognized as such from the raw XMT data. The most reasonable explanation to this failure to clearly identify the pore space is that resolution of the XMT scans (approximately 1 µm) was insufficient. Figure 3, which shows the submicron structure of two different hydrated cement pastes, offers some support of this hypothesis. From these figures it appears that a resolution in the micrometer range is insufficient to capture the complex dendritic structures that form as a result of hydration. Moreover, this particular structure suggests that a voxel which has been identified as belonging to the pore space due to a low grayscale level in fact may contribute significantly to the effective resistance against diffusion. As
Figure 3. Submicron structure of two different hydrated cement pastes. After Buenfeld et al., 2007 (left) and Tritthart and Haussler, 2003 (right).

Table 1. Cement pastes analyzed. The data sets are from from http://visiblecement.nist.gov. The average effective diffusivities are calculated as ![]()
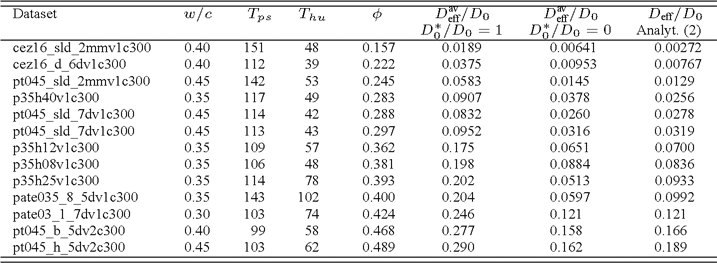
Figure 4. Comparison between computed effective diffusivities and analytical estimate (2).

such, assigning a constant diffusivity to the ‘pore space’ voxels may lead to significant overestimates of the effective diffusion coefficient.
In an attempt to remedy this predicament, local diffusivities less than the free diffusivity were assigned to the intermediate gray scale voxels. This was done via a simple linear relationship so that the local pore diffusivities were taken as
(3) ![]()
where Dp is the pore diffusivity, D0 is the free diffusivity, D10 is a new constant that will be referred to as the ‘linear grayscale diffusivity’, G is the grayscale (0 ≤ G ≤ 42), and T = 42 is the pore/solid threshold value. In other words, pores with a grayscale count of 0 (6.7% in total) are assigned the free diffusion coefficient whereas the magnitude of the local diffusivities will decrease linearly to D10 at the threshold level.
In order to probe the validity of the proposed grayscale-pore diffusivity rule (3), we have analyzed a total of 13 different cement pastes as summarized in Table 1 and Figure 4. Remarkably, for the most part, the diffusivities resulting from setting the grayscale diffusivity equal to zero, i.e. by letting the pore space diffusivity vary linearly with the grayscale value from G = 0 to G = Tps, are in excellent agreement with the analytical/empirical formula (2) of Garboczi and Bentz (1992). It this appears reasonable to conclude that the proposed empirical rule has general validity, at least for the cement pastes in the NIST data set. As for application to other data sets, the rule would probably in most cases furnish a reasonable first estimate.
The success of the proposed procedure for correcting for submicron features motivate the search for a more physical means of constructing such laws. From the wide range of pastes considered (see Table 1) it appears that the rule in the present case is relatively insensitive to porosity, water/cement ratio, hydration time, etc. We would, however, expect it to be a function of the particular type of cement paste (chemical composition of the cement, additives, etc) and of the XMT settings (resolution, beam energy, etc). Ultimately, however, it could be envisioned that the submicron features actually are resolved. With recent advanced in nano-CT this could well be a reality in coming years. One would then use the effective nanoscale diffusivity as input to microscale models such as the ones considered in the present paper.
4. Conclusions
The problem of extracting effective diffusivities of cement pastes on the basis of X-ray microtomography images has been considered. A previously developed computational homogenization framework has applied to selected data sets. With the resolution of the selected data sets (approximately 1 µm), important submicron features are not resolved and it is necessary to perform a ‘correction’ to account for unresolved submicron features. This is done be ascribing the pore space a diffusivity less than the free diffusivity. In particular, it is found that a linear variation of the pore phase diffusivity with grayscale level furnishes reasonable results.
5. References
Andrade C., “Calculation of chloride diffusion coefficients in concrete from ionic migration measurements”, vol. 23, p. 724–742, Cement and Concrete Research, 1993.
Barberon F., Korb J. P., Petit D., Morin V., Bermejo E., “Probing the Surface Area of a Cement-Based Material by Nuclear Magnetic Relaxation Dispersion”, vol. 90, no. 116103, Physical Review Letters, 2003.
Bentz D. P. et al., “Microstructure and transport properties of porous building materials. II: Three-dimensional X-ray tomographic studies”, vol. 33, p. 147–153, Materials and Structures, 2000.
Bentz D. P. et al., “The Visible Cement Data Set”, vol. 107, p. 137–148, Journal of Research of the National Institute of Standards and Technology, 2002.
Buenfeld N., “Concrete Durability Group. Secondary Electron Imaging”, 2007.
Friedmann H., Amiri O., Ait-Mokhtar A., Dumargue P., “A direct method for determining chloride diffusion coefficient by using migration test”, vol. 34, p. 1967–1973, Cement and Concrete Research, 2004.
Garboczi E. J., Bentz D. P., “Computer Simulation of the Diffusivity of Cement-Based Materials”, vol. 27, p. 2083–2092, Journal of Materials Science, 1992.
Karim M. R., Krabbenhoft K., “Extraction of effective cement paste diffusivities from X-ray microtomography scans”, under review, 2009.
Knackstedt M. A. et al., “Elastic and transport properties of cellular solids derived from three-dimensional tomographic images”, vol. 462, p. 2833-2862, Proceedings of the Royal Society A, 2006.
Krabbenhoft K., Hain M., Wriggers P., “Computation of Effective Cement Paste diffusivities from Microtomographic Images”, p. 281–297, Kompis V., Ed., Composites with Micro- and Nano-Structure, Spinger, 2008.
Krabbenhoft K., Krabbenhoft J., “Application of the Poisson-Nernst-Planck equations to the migration test”, vol. 38, p. 77–88, Cement and Concrete Research, 2008.
Promentilla M. A. B., Sugiyama T., Hitomi T., Takeda N., “Characterization of the 3D pore structure of hardened cement paste with syncrotron microtomography”, vol. 6, p. 273–286, Journal of Advanced Concrete Technology, 2008.
Promentilla M. A. B., Sugiyama T., Hitomi T., Takeda N., “Quantification of tortuosity in hardened cement pastes using synchrotron-based X-ray computed microtomography”, vol. 39, p. 548–557, Cement and Concrete Research, 2009.
Tang L., Nilsson L. O., “Rapid determination of the chloride diffusivity in concrete by applying an electric field”, vol. 89, p. 49–53, Cement and Concrete Research, 1992.
Torquato S., Random Heterogeneous Materials, Springer, 2002.
Tritthart J., Häußler F., “Pore solution analysis of cement pastes and nanostructural investigations of hydrated C3S”, vol. 33, p. 1063–1070, Cement and Concrete Research, 2003.
