Two Less-Used Applications of Petrophysical CT-Scanning
ABSTRACT. Computerized Tomography (CT) has been used by oil and service companies for over 25 years for looking inside rocks. Although the first applications were for viewing multiphase fluid flow, qualitative and primarily visual characterization, such as examination for mud invasion, inclusion and heterogeneity, soon took precedence. This paper discusses two CT applications which yield quantitative 3D maps of physical attributes pertinent to the core analyst. A bulk density map is derived from dual-energy scans and saturation and/or porosity maps are derived from multiple scans of multi-phase flow. While these applications are more complex than the qualitative ones, careful scanning and appropriate software can get rewarding results. Step-by-step instructions are shown in this paper for applying these two features with appropriate examples and also common pitfalls with precautions and some remedies are discussed.
KEYWORDS: CT, tomography, dual energy, core characterization, saturation mapping
1. Introduction
The petroleum industry has used Computerized Tomography (CT) scanners to evaluate petrophysical and fluid flow properties of reservoir rocks in a nondestructive and cost-effective manner. CT helps identify lithology, measure density and porosity, evaluate formation fluid damage; and it allows viewing of multiphase flow in rocks. Detailed reviews of the applications of CT in rock and fluid research can be found in the literature (Vinegar and Wellington, 1987; Wellington and Vinegar, 1987; Kantzas, 1990; Akin and Kovscek, 2001). Overall, the petroleum industry applications of CT can be divided into two major areas: core characterization and fluid flow visualization. CT serves as a powerful tool for fluid flow visualization in cores and it is widely used in coreflooding tests to quantify multiphase flow behavior and to observe the effect of treatment fluids. In this paper we focus mainly on two aspects of CT-scanning: 1) dual-energy CT for core characterization and 2) saturation calculation during multiphase flow.
2. Dual energy CT for core characterization
In dual-energy CT-scanning, the object is scanned twice at the same location, using a high- and a low-energy setting. By selecting the high- and low-energy settings, one can take advantage of the two predominant x-ray interactions with matter namely, the photoelectric absorption (predominant at low-energies) and the Compton scattering (predominant at high-energies). These, in turn, have different dependence on effective atomic number (Zeff) and electron density. It is possible to calculate the Zeff and electron density of an object by scanning it at two x-ray energies with sufficient energy separation. Wellington and Vinegar (1987) suggested using 100 kV as the threshold value for the two effects. Since most medical scanners are limited to a maximum of 140 kV, the latter can be used as the high-energy setting for scanning rocks. Although many medical scanners have settings of 90, 80, 70 or even 60 kV as the lowest energy, it is very difficult to pass enough x-rays through a typical reservoir rock such as a carbonate at energies below 70 kV. The same is true for most microfocus CT-scanners. The following equation, modified from Wellington and Vinegar (1987), is most widely used in calculating dual-energy based true density (ρ) and atomic number (Z).
[1] ![]()
where μ is the linear attenuation coefficient (the parameter measured by a CT-scanner), E is the X-ray energy, a is the Klein-Nishina coefficient, n is an exponent for the Z (with different values used by researchers for n such as 3, 3.1, 3.6 and 3.8), and b is a constant. Equation [1] is highly non-linear and calculation of the energy-dependent coefficients a and b becomes uncertain due to the polychromatic nature of the x-ray beams and due to unknown effective energies at the high and low voltage settings. Vinegar and Kehl (1988), Coenen and Maas (1994), Siddiqui and Khamees (2004) suggest using techniques involving scanning “standards” of known ρ and Zeff (applicable to compounds and mixtures) at the same conditions and their procedures yield true density of the unknown material and the Zeff that can be used for identifying major minerals in core samples or rock fragments (cuttings). The dual-energy CT-scanning involves calculating, for a fixed (usually circular) region of interest (ROI) of each slice, the average μ (attenuation) or CTN (normalized attenuation, in Hounsfield Units, output of a medical CT-scanner), at two energies, which are then converted to true ρ and Zeff. Software toolkits are now available that can make it convenient to interact with variables in the dual-energy equations for the two- or three-dimensional objects. PV-Wave and Matlab are examples of languages which can do this and in addition, they have the means of making a sophisticated graphical user interface (GUI) and they have extensive math libraries for computation. The code can readily be used on Windows, Linux, and UNIX operating systems. With this approach, CT-scan data analysis programs are developed that are portable, convenient to use and rapid to develop, with good performance. One such program is VoxelCalc, is used here to demonstrate the ease of processing dual-energy and saturation data.
2.1. Scanning considerations-spatial repeatability
Since dual-energy CT-scanning involves scanning the core at the same exact locations twice, each time with a different energy, and since most scanners are not capable of taking these two scans simultaneously, it is very important to have a scanning table (or a rotation stage, for micro CT) with good repeatable positioning accuracy. Also, in order to prevent displacement due to vibration during table (or rotor) movement, the sample itself or its holder (core holder) must be harnessed firmly for the scans. Additionally the table (or rotating stage) should have sufficient capacity to support heavy loads with minimum deflection.
2.2. Scanner calibration for rock – beam hardening
Calibration of the scanner is performed to reduce the artifact of “beam hardening”, a cupping effect seen on objects due to preferential absorption of the lower energy X-rays from a polychromatic source. Figures 1a illustrates beam hardening, caused by inappropriate calibration, before (left) and after (center) postscan adjustment. The corresponding profiles are also shown in Figure 1a (right). The surface renderings in Figure 1b show the same cupping effect before and after the adjustment. The software used applies a radial curve fit on the slices which generally works well if the objects within the slices are not too heterogeneous.
Figure 1a. Example of beam hardening, before adjustment (left), after adjustment (center), and the corresponding profile images (right)
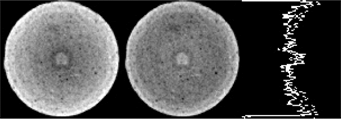
Figure 1b. Surface renderings of image with beam hardening artifact before (left) and after (right) adjustment
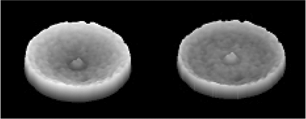
Phantoms with densities and chemistry approximating rocks to be scanned are used to measure the amount of correction, or flattening applied to each slice. Typically, the industry uses fused quartz phantoms for sandstones and Macor phantoms for carbonates, rather than the medical water phantom. Calibration should be performed for each of the major mineral types, for each energy level, and then applied at scan time. Placing metal filters in front of the X-ray source, packing the sample in some special media, and using a core holder can reduce these artefacts; however, one must take care to assure good penetration through the sample. It should be noted that even with all the precautions beam hardening cannot be totally avoided. Post-scan adjustments by software can flatten the slices without a phantom image, but this pre-scan calibration is far better.
2.3. Core preparation
For dual-energy analysis, which is very helpful to understand the mineral contents and distribution in rock samples, cylindrical shape is preferred (to avoid the X artefacts, seen in Figure 2a).
Figure 2a. The X-artifact (after Akin and Kovscek, 2001)

Figure 2b. A spotty image due to insufficient X-ray energy
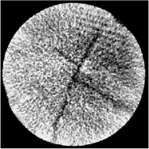
If it is desired to measure the properties at reservoir condition (at higher temperature and pressure than ambient), then the core must be put inside a core holder, which is typically made of aluminum or aluminum wrapped with carbon fiber tapes. In general the core holder pre-hardens the beams but they can potentially reduce the penetration capability in the case of large or dense samples. For larger samples and for samples kept inside core holders, the ability of X-rays to take sharp images, especially at the low-energy setting must be tested. Figure 2b shows a CT slice for a 4” diameter sandstone core for which the X-ray energy was not enough, resulting in a spotty image. For these cases either choosing a smaller sample size if possible, or switching to a higher energy setting, while still staying within the domain of photoelectric dominance, is recommended.
2.4. Standard materials
For success of the dual-energy procedure, a good set of dual-energy “standards” must be used. These standards are homogeneous, solid materials (non-porous), for which the bulk density and Zeff must be accurately known. The standards should preferably have the same diameter as the core sample. The exact bulk density can be easily calculated using the weight and bulk volume of each standard. For pure materials with known compositions Zeff can be calculated (Siddiqui and Khamees, 2004). VoxelCalc lists several dual-energy standards that have been used successfully for analyzing reservoir cores. They are – calcite, dolomite, quartz (both crystalline and fused), NaCl, Teflon, Kel-F, aluminum 6061, water, doped water for which typical values of Zeff and ρ are provided. There is an option to add up to three new standards and to edit the provided Zeff and ρ data to incorporate data for the actual standards used. If the standard is not homogeneous and if it contains impurities, serious errors may result from it. Composition information can sometimes be verified by using X-ray diffraction and scanning electron microscopy techniques.
Figure 3a. Scanning of dual energy standards

Figure 3b. Reading of CT numbers of dual energy standards

Current industry practice is to scan these standards, which are typically in the form of ½” (1 cm) diameter cylinders (the liquid standards such as water and doped water are usually placed inside small cylinders) by placing them around the outside of the core holder (Figure 3a). This configuration can yield good results if extreme care is taken in applying small centered regions as indicated by the white areas in Figure 3b when extracting the mean CT values. The regions must be congruent for the high and low energy CT values obtained. An alternative way is to use short calibration standards (about ½” to 1” long, preferably all having the same length), taped together and scanned at the same conditions as the core sample (at the same energy and ‘environmental’ conditions, i.e., the same calibrations and during the same scanner power-up session).
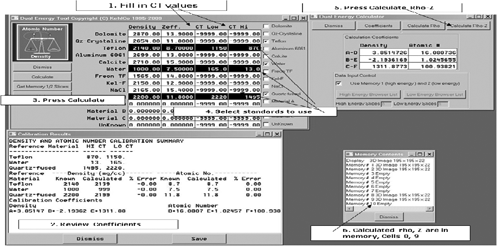
2.5. Obtaining coefficients and solving for density and effective atomic number
The first step in conducting dual-energy data analysis is to generate the dual energy coefficients. The procedures used by Vinegar and Kehl (1988) and Siddiqui and Khamees (2004) both use six coefficients (three for Zeff three for ρ), which are calculated based on the attenuation data for the standards at the high- and low-energy settings. Although several standards are scanned, data from a minimum of three standards are needed to generate the six coefficients. There is no standard procedure for selecting three standards out of the six or seven scanned during the process. Ideally, any three standards that have properties similar to the minerals present in the core should give the best result. In reality, finding three such standards is quite difficult and sometimes an odd combination may end up giving better results. We suggest using a trial-and-error procedure in which the coefficients are used to predict the Zeff and ρ for a homogeneous core plug (Berea and Fontainebleau sandstone, Indiana limestone, etc.) for which these data are known, before using the coefficients for finding these properties for the unknown samples. VoxelCalc offers the option to calculate the coefficients quite easily. CT values for standards are obtained by using the ROI tool which obtains the mean with a circle on a selected slice. This is done for both high and low energies, and the data are then entered into the calibration table for the appropriate material (Figure 4). At least three standards should be used; however, VoxelCalc allows data from more standards in which a regression-based method is used to determine the coefficients.
Figure 4. Calculating and applying coefficients for determining Zeff and ρ data
3. Saturation calculation during multiphase flow
Visualizing saturation changes in core samples during a laboratory coreflooding test was almost unknown before the use of CT. Fluid flow visualization with CT almost always involves the use of one or more radiopaque tracers (also called dopants) containing high atomic number ions (e.g. I−, Br−, etc.). The dopants provide sufficient contrast between the various fluid phases which allows us to view and quantify saturation distribution and its changes, gravity and viscous effects, trapping and bypassing, effects of heterogeneity on flow, etc. The concentration of the dopant depends on the porosity of the core, typically a higher concentration is needed for cores with a lower porosity. For two phase (oil-water) flow typically the water phase is doped with NaI, KI, KBr, NaBr, etc. but for three phase flow, two of the phases are doped. Vinegar and Wellington (1987) provide details of the use of dopants.
3.1. Scanning considerations
All saturation monitoring experiments require the use of a core holder. Like the dual-energy case, having good positioning accuracy for the table and keeping the core holder fixed with the table are of utmost importance for accurate calculation of saturations. For slight movements, some post-scan alignment capability is always useful. Although the presence of core holder pre-hardens the x-rays, beam-hardening can still potentially affect the data, especially when the pore space is saturated with a high concentration of dopant. During scanning after each stage of coreflooding, the core plug or plugs should be always scanned in the same direction (inlet to outlet), with full coverage. The scanning speed should be fast enough to capture all the fluid related changes, instructing the scanner to avoid reconstructions generally speeds up image acquisition. Before or after the coreflooding, all calibration standards (typically plastic bottles containing oil and water with the exact concentration of dopants used for flowing through the core) must be scanned using the same operating parameters and under same environmental conditions. A typical two-phase coreflooding experiment can have several stages – pulling vacuum, saturating with doped water, flowing doped water through core to ensure 100% saturation (images from this stage are typically used as reference for the image subtraction calculations later), displacing water by oil (drainage) in order to bring the core to its irreducible water saturation (Swir), displacing oil by water (imbibition) to bring it to its residual oil saturation (Sor), etc. The core is scanned at the end of each displacement stage and also at several intermediate stages. The images from scans at various stages of water saturation are used to calculate in-situ saturations.
3.2. Image processing
Although average attenuation data for slices from different scan sequences are sufficient to calculate in-situ saturations, the ability of some image processing programs such as VoxelCalc to conduct a pixel-by-pixel subtraction opens many possibilities. Matrix-subtracted images allow the observation of minor flow anomalies, which helps our understanding of multiphase flow, especially in heterogeneous porous media.
Figure 5a. Wet scan slice
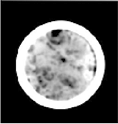
Figure 5b. Dry scan slice
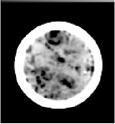
Figure 5c. Difference slice

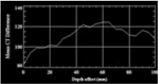
Typical image processing workflow includes subtracting from the slices of the core when it is 100% saturated with doped brine (e.g. the wet scan slice in Figure 5a), the slices with the under vacuum (e.g. the dry scan slice in Figure 5b), which results in the matrix-subtracted slices (e.g. the dfference slice in Figure 5c). The latter can give a clear picture of fluid distribution in cores, separating the more-porous areas from less-porous areas, which are otherwise very hard to detect from simple slice images at varied stages. In addition to providing various options for array calculations, VoxelCalc also offers circular cropping, generation of horizontal and vertical slabs (Figures 6a and 6b) and saturation profiles (Figure 6c) and saving of the matrix-subtracted images as image stacks, which can then be brought into VoxelCalc or other advanced image processing programs to make animations of multiphase flow in porous media.
Figure 6a. Horizontal slab

Figure 6b. Horizontal slab

Figure 6c. Saturation profile
4. Conclusions
In this paper we have demonstrated the use of two applications – dual-energy CT-scanning and saturation calculations using CT with the help of appropriate image processing software. These data are very useful in petrophysical studies of reservoir rocks and small cuttings. Although examples shown are for medical scanners, the procedures can also be applied to micro CT-scanning. The ability to estimate the mineral content and to observe flow and distribution of fluids during coreflooding operations can enable better decisions about production and environmental remediation.
5. References
Akin, S. and Kovscek, A.R., “Use of Computerized Tomography in Petroleum Engineering Research,” Annual Report of SUPRI TR 127, Stanford University, Stanford, CA, August 2001, pp. 63-83.
Coenen, J.G.C., Maas, J.G., “Material Classification by Dual-Energy Computerized X-ray Tomography,” Proceedings of the International Symposium on Computerized Tomography for Industrial Applications, Berlin, Germany, 1994, pp. 120-127.
Kantzas, A, “Investigation of Physical Properties of Porous Rocks and Fluid Flow Phenomena in Porous Media Using Computer Assisted Tomography,” In Situ, Vol. 14, No. 1, 1990, p. 77.
Siddiqui, S. and Khamees, A.A., “Dual-Energy CT-Scanning Applications in Rock Characterization,” SPE paper No. 90520, presented at the 2004 SPE Annual Technical Conference and Exhibition held in Houston, Texas, 26-29 September 2004.
Vinegar, H.J. and Kehl Jr., R.P., User Guide for Computer Tomography Color Graphics System – CATPIX, Shell Bellaire Research Center, Houston, TX, 1988, 85 pp.
Vinegar, H.J. and Wellington, S.L., “Tomographic Imaging of Three-Phase Flow Experiments,” Rev. Sci. Instrum., January, 1987, p. 96.
Wellington, S.L. and Vinegar, H.J., “X-Ray Computerized Tomography,” Journal of Petroleum Technology, August 1987, p. 885.
