3D and Geometric Information of the Pore Structure in Pressurized Clastic Sandstone
ABSTRACT. The three-dimensional geometry and connectivity of pore space play a fundamental role in governing fluid transport properties of porous media. The spatial and three-dimensional information of pore geometry is difficult to obtain under air and pressurized conditions. To quantify the flow-relevant geometric properties of the pore structure in clastic sandstone, we introduce the three-dimensional medial axis (3DMA) method. We verified the applicability of the 3DMA method for glass beads aggregate as porous material. We present the effect of the hydrostatic pressure on permeability using the transient pulse method and giving a quantitative characterization of pore distributions in intact clastic sandstone and clastic sandstone pressurized to 25 MPa.
KEYWORDS: pore, throat, 3-dimentional geometry, permeability, tortuosity, medial axis
1. Introduction
Sedimentary rocks are named and classified mainly on the basis of their texture and composition. Sedimentary rocks classified as being clastic are composed mainly of broken and worn fragments of preexisting minerals, rock particles that were carried to the site of deposition by moving agencies such as streams, wind, waves, and glaciers, and there cemented. Sandstones are fundamentally clastic in origin.
Porosity and permeability are two primary factors controlling the movement and storage of fluids in rock and sediments. The mechanical and hydraulic properties of porous rocks are a major and common concern in various scientific and engineering fields. The permeability and specific storage of rocks and sedimentary layers deep underground are important parameters for problems such as those related to the evaluation of buried natural gas and oil, CO2 aquifer storage, and various kinds of waste storage.
The permeability of a geologic material is dependent on the porosity of the material and the degree of connectivity between pores. The specific storage of geologic materials is dependent on the porosity of the material and the compressibility of both the material and the included fluid; accordingly, both the permeability and specific storage of geologic materials vary over wide ranges. For example, the permeability of geologic materials may vary from 0.2 m/s for gravel to less than 10−11 m/s for clay and intact rock, representing variation by a factor of 1010. The general equation that describes the transient pulse test method has been used to quantitatively evaluate transient variations in hydraulic head and the transient distributions of hydraulic gradient within a test specimen.
Takahashi et al. (2006) measured porosity changes by means of mercury-injection porosimetry and a gas adsorption method for Shirahama sandstones that were deformed under various confining pressures and pore pressures. The brittle and fully ductile deformation regimes are associated with distinct patterns of volumetric strain change measured by displacement transducers and pore volume change evaluated from the pore fluid volume flowing out of or extracted from the specimen. They focused on the correlation of inner structural changes, especially those on a microscopic scale, with mechanical deformation using permeability, total porosity, and BET surface-area measurements. Under higher confining pressures, the specimens behave in a fully ductile manner, and the volumetric strain determined from displacement-transducer measurements and pore volume change shows persistent compaction throughout the experiments. They confirmed that the total porosity determined by means of mercury-intrusion porosimetry increases with increasing confining pressure, and the BET surface area of the pore space obtained using the gas adsorption method supports the porosity increase.
The total porosity and pore size distribution in atmospheric sandstone have been obtained through mercury-injection porosimetry and the gas adsorption method generalized as the BET method. However, three-dimensional information of the pore geometry is difficult to obtain under ambient air and pressurized conditions. Thus, we try to investigate the pressure dependence on geometrical information of pore space in rock specimen by means of micro focus x-ray CT data. In this paper, we use the three-dimensional medial axis (3DMA) method of Lindquist et al. (2000) to quantify the flow relevant geometric properties of the pore structure in Shirahama sandstone, clastic sandstone in Japan. At first, we obtain three-dimensional data for different sizes of glass beads by microfocus x-ray CT, and verify 3DMA method for application to glass beads as representative of porous media. In addition, we present the quantitative characterization of each distribution of pore geometry for intact Shirahama sandstone and Shirahama sandstone pressurized to 25 MPa.
2. Inner pore structure and permeability of comparison Berea sandstone and Shirahama sandstone
Most sandstone is composed of quartz and/or feldspar because these are the most common minerals in the Earth’s crust. Sandstones are fundamentally clastic in origin. They form from cemented grains that may either be fragments of pre-existing rock or mono-minerallic crystals. The most common cementing materials are silica and calcium carbonate, which are often derived from the dissolution or alteration of sand after it is buried. The environment where it is deposited is crucial in determining the characteristics of the resulting sandstone, which include its grain size, sorting and composition, and the rock geometry and sedimentary structure.
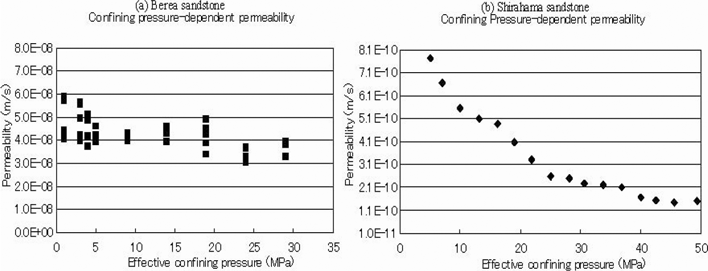
Berea sandstone is fine grained, but the grains are angular rather than rounded, which makes this sandstone an ideal grindstone and abrasive. It has been quarried in many areas as a building stone and was used for foundations, sidewalks, bridge abutments, and buildings. The relatively high porosity of about 18% and permeability of Berea sandstone makes it a good reservoir rock. Berea sandstone is widely used as a standard specimen in oil reservoir engineering. Total porosity is about 18% and rather large pores are dominant. Figure 1(a) shows the permeability evolution for increasing hydrostatic pressure. Permeability was measured with a transient pulse technique to the method by Brace et al. (1968), Hsieh et al. (1981) and Neuzil et al. (1981). The permeability is calculated from the recovered pulse decay across the specimen (Zhang et al. 2000a, b). It is seen there is rather high permeability and low dependency on hydrostatic pressure.
The tested sample of Shirahama sandstone was obtained from the Kii Peninsula, Wakayama prefecture, central Japan. The sandstone is Miocene sedimentary rock that consists mainly of quartz grains (44.23%) and rock fragments (46.41%) that are aggregations of various kinds of minerals. The quartz grains have an average size of about 150 µm. The rock fragments have irregular shapes and are relatively easy to deform or crush. The sandstone is rich in rock fragments and has high roundness, low total porosity and rather small pores below a micron scale, and high hydrostatic pressure dependency on permeability reduction (Figure 1(b)). The pre-existing pores are dominantly approximately 1 micron in size, and the total porosity is about 13%. For this clastic sandstone of Shirahama sandstone, we carried out image processing using X-Ray CT volume data and the three-dimensional axis analysis method, and investigated the difficulty of the segmentation treatment for clastic rich sandstone with a rather small pore size and low porosity.
Figure 1. Permeability as functions of hydrostatic pressure of Berea sandstone (a) and Shirahama sandstone (b). The permeability is measured by the transient pulse method
3. Outline of the 3DMA method
Lindquist and Venkatarangen (1999) developed the 3DMA computational package as a tool for analyzing the geometry of the pore and grain phases in three-dimensional CT data. Using this package, we can obtain the spatial distributions for pore and throat sizes, coordination number, tortuosity, and other geometric relations between pores and throats. In general, CT images of porous media are grayscale images and have a bimodal population, one mode corresponding to the signal from the pore space and the second to the signal from the grain space. As we are interested in the pore structure, an appropriate segmentation procedure is required to quantify the geometry of the pore space. The most suitable threshold procedure is selected to match a predetermined bulk density and porosity of the porous medium. In the 3DMA package, the kriging-based algorithm is used to segment the voxel images. The medial axis for a sphere is a straight line passing through the center point, and that for a cylinder is the axis of rotational symmetry. The medial axis for any n-dimensional object can be found using an algorithm equivalent to a “burning algorithm” (see Lindquist et al., 1996).
Figure 2 is a two-dimensional illustration of the medial axis behavior of two nodal pores. A throat is defined as a local minimum of the cross-sectional area in a channel. For an object in a spatial continuum, the medial axis is a network of paths and vertices unless the object contains embedded cavities, in which case the medial axis also contains surface segments. For digitized objects, the medial axis consists of digitized paths corresponding to a line of connected voxels, digitized vertices corresponding to a cluster of one or more voxels, and possibly digitized surfaces corresponding to a sheet of voxels. The usual conceptual model divides the void space of a porous medium into nodal pores connected by pore channels. Nodal pores are located at multigrain junctions. Roughly equidimensional in geometry, these nodal pores are joined to one another by pore channels, which include microcracks situated along interfaces between two neighboring grains and tubular pores along three-grain edges.
Figure 2. 2-dimensional illustration of Medial Axis behavior
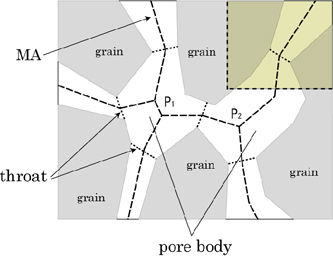
Figure 3 shows the original CT data and an example of medial axis analysis for the packing of glass beads with 600 µm diameters. We can visually confirm the accuracy of the medial axis analysis. The medial axis is affected by the flow channel, percolating backbone, and flow path in addition to other factors.
Figure 3. 3-dimensional image of Medial Axis in grass beads with 600 µm diameter: (a) 3-dimensional original CT data (b) 3-dimensional pore space image extracted from CT data (c) 3-dimensional medial axis image calculated from pore network data

4. Microfocus x-ray CT apparatus and geometric information of intact and stressed Shirahama sandstone
A new pressure vessel was developed to simultaneously supply both the confining pressure and pore pressure to a rock specimen with a 10 mm diameter and 20 mm length. To determine a change to the inner structure of a rock specimen under hydrostatic pressure, we took three-dimensional images of stressed Shirahama sandstone by microfocus x-ray CT. The hydrostatic pressure was raised to 25 MPa, which generally corresponds to the stress state at 1,000 m depth.
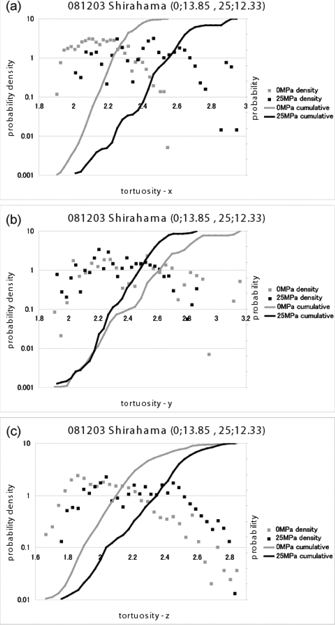
Figure 4 shows various images for the intact (upper low) and stressed (lower low) samples; (a) (b) 3 dimensional original CT volume data, and (b) (d) the 3DMA network. Figure 5 shows the measured distributions of (a) throats, (b) pores, and (c) coordination numbers for intact and stressed samples. The measured frequencies for throats and pores decreased remarkably under the stressed condition. It is clear that permeability reduction as the hydrostatic pressure increases is attributable to the decrease in the population of pores with a radius of 20–90 µm, decrease in the population of throats with a radius of 10–50 µm, and increase in tortuosity in the X and Z directions. This phenomenon has already been confirmed by theory and many experiments, but the three-dimensional geometry of throats and pores has not been investigated in detail. Ultimately, we can obtain three-dimensional visualizations. Figure 6 shows the changes in tortuosity in three directions for intact and stressed samples. In each direction, the tortuosity was greater under the stressed condition. Hydrostatic pressure decreased the pore size, throat size, and coordination number in Shirahama sandstone. Permeability reduction under pressurization to 25 MPa hydraulic pressure is attributed to these inner structural changes.
Figure 4. Calculated observations under intact (upper low) and stressed (lower low) state. (a)(c) 3-dimensional original CT data; (b)(d) 3-dimensional medial axis image calculated from pore network data

Figure 5. Measured distributions of throat (a), pore (b) and coordination number (c)
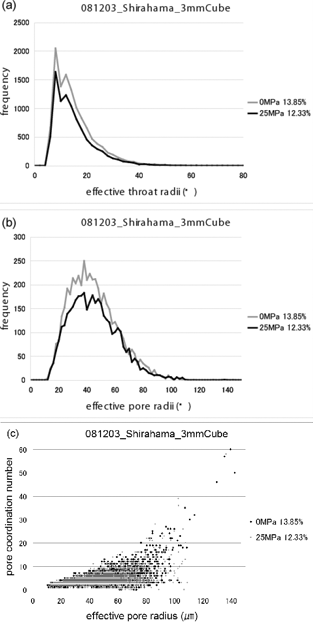
Figure 6. Tortuosity distributions for X, Y and Z direction. Z axis corresponds to horizontal direction
5. Conclusion
Porosity and permeability are two primary factors that control the movement and storage of fluids in rock, especially clastic sandstone in the case of Japanese fields. Permeability experiments were conducted under hydrostatic stress to 25 MPa to investigate geometric differences in Shirahama sandstone. The permeability consistently decreased with increasing hydrostatic pressure and with decreasing volumetric strain. To quantify the flow-relevant geometric properties of the pore structure in Shirahama sandstone, we used the 3DMA method of Lindquist et al. (2000) and verified three-dimensional data for different stress conditions obtained by microfocus x-ray CT. We verified the results obtained using the 3DMA method and measured the distributions of pore size, throat size, channel length and coordination number as well as correlations between pore geometry and throat geometry. In addition, we presented the quantitative characterization of each distribution for intact Shirahama sandstone and Shirahama sandstone pressurized to 25 MPa. It is clear that the permeability reduction due to increasing hydrostatic pressure is caused by a decrease in the population of pores with a radius of 20–90 µm, decrease in the population of throats with a radius of 10–50 µm, and increase in the tortuosity in the X and Z directions in stressed Shirahama sandstone.
6. References
Lindquist W. B., Lee S.-M., Coker D. A., Jones K., W., Spanne P., “Medial axis analysis of void structure in three-dimensional tomographic images of porous media”, Journal of Geophysical Research, vol. 101, no. B4, 1996, p. 8297-8310.
Lindquist W. B., Venkatarangan A., “Investigating 3D geometry of porous media from high resolution images”, Physics and Chemistry of the Earth Part A, vol. 25, no. 7, 1999, p. 593-599.
Lindquist W. B., Venkatarangan A., Dunsmuir, J., Wong T.-F., “Pore and throat size distributions measured from synchrotron X-ray tomographic images of Fontainebleau sandstones”, Journal of Geophysical Research, vol. 105, no. B9, 2000, p. 21509-21527.
Brace, W. F., Walsh, J.B., and Frangos, W. T., “Permeability of granite under high pressure”, Journal of Geophysical Research, vol. 73, no. 6, 1968, p. 2225-2236.
Hsieh, P, A., Tracy, J. V, Neuzil, C, E.,Bredehoeft, J, D., and Silliman, S, E., “A transient, laboratory method for determing the hydraulic properties of tight rocks – I theory”, International Journal of Rock Mechanics and Minig Sciences & Geomechanics Abstracts, vol. 18, no. 3, 1981, p. 245-252.
Neuzil, C. E., Cooley, C., Silliman, S. E., Bredehoeft, J. D., and Hsieh, P. A., “A transient laboratory method for determining the hydraulic properties of tight rocks – II. application”, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, vol. 18, no. 3, 1981, p. 253-258.
Zhang, M., Takahashi, M., Morin, R. H., and Esaki, T., “Evaluation and application of the transient-pulse technique for determining the hydraulic projectiles of low-permeability rocks – Part 1:theoretical evaluation”, Geotechnical Testing Journal, vol. 23, no. 1, 2000a, p. 83-90.
Zhang, M., Takahashi, M., Morin, R. H., and Esaki, T., “Evaluation and application of the transient-pulse technique for determining the hydraulic projecties of low-permeability rocks – Part 2: experimental application”, Geotechnical Testing Journal, vol. 23, no. 1, 2000b, p. 91-99.
