Segmentation of Low-contrast Three-phase X-ray Computed Tomography Images of Porous Media
ABSTRACT. X-Ray Computed Tomography (XCT) is an important tool to study porous-media microstructure and fluids present within the void space. In the presence of multiple fluid phases (e.g. air-water in soil science or oil-water-gas in petroleum engineering), the contrast between the fluid phases becomes important for accurate image segmentation. In some cases (e.g. a white light source or low flux), it is not possible to illuminate one of the fluid phases. The result is then a single image containing multiple phases that may contain overlapping peaks of the fluid phases due to little difference in the absorption coefficients. Building upon work done in medical-image-processing research, we have adopted a nonlinear anisotropic diffusion technique to remove noise from the XCT image that also leads to improved peak separation in the image histogram. The noise-free image is the then segmented using indicator kriging and the results are compared with segmentation results obtained using absorption-edge imaging.
KEYWORDS: porous media, segmentation, three phase, anisotropic diffusion, indicator kriging
1. Introduction
In 3D imaging of porous media using XCT, attenuation coefficients of the chemical species and phase density dictate the x-ray absorption and result in a grayscale-absorption-image. Solids present in the natural porous media typically contain minerals with high x-ray attenuation resulting in a grayscale image with good contrast between the solid and void phases. For porous media systems where more than one fluid phase is present, a small amount of chemicals with high attenuation coefficients can be added to one of the fluid phases to increase the contrast in the resulting grayscale-absorption-image. Selective illumination of one or more doped fluids is possible using a monochromatic x-ray beam through the selection of specific energies above and below the element-specific x-ray absorption edge(s). However, this is not possible when using a polychromatic x-ray beam resulting in a single image containing two or more phases.. Accurate segmentation of the phases is critical for accurate calculation of interfacial areas, curvatures, etc.
The segmentation of an image is performed to partition the image into regions with similar predefined criteria such as similarity of the intensity values, connected components or bounding edges. Edge-based techniques include level set, active contour and watershed techniques (Sheppard, Sok, and Averdunk, 2004 and Vincent, Soille 1991). Histogram-based techniques such as simple and multiple thresholding, clustering and Indicator Kriging operate based on the discontinuity or abrupt change in the intensity values in the histogram. The accuracy of segmentation techniques is affected by the noise present in the image. Noise in XCT images can arise from various sources, such as scattered x-ray photons impinging on the detector to create speckle noise, imperfections in the detector causing ring artifacts or error in the reconstruction causes blurring (Herman, 1980). Impurities in natural samples and little separation in attenuation values of phases can lead to blurring and merging of two or more peaks in the image histogram. The main challenge for any noise removal algorithm is to be able to distinguish the phase edges and small features in the image and selectively alter only the noisy voxels. The literature contains many methods ranging from simple low pass averaging filters such as the Gaussian filter and the median filter to process-based filters such as anisotropic diffusion and wavelet transform. Here, we demonstrate the application of nonlinear anisotropic diffusion for de-noising of an image of a multiphase porous media system and threshold indicator kriging for segmentation of the phases.
2. Anisotropic diffusion
The diffusion process equilibrates fluctuations in a property to its neighborhood. In image processing, the noise in a grayscale image can be visualized as the fluctuations in the grayscale values. The diffusion equation (equation [1]) is applied to the grayscale (intensity) values I(x, y, z) to equilibrate the noise to its surrounding neighborhood. Perona and Malik (Perona and Malik, 1990) proposed a non-linear isotropic diffusion approach where the diffusion coefficient is an inverse function of the local image gradient (equation [2]). This approach causes the diffusive flux to be minimized across the edges since image gradient is maximum at the phase edges. The tensor form of the diffusion coefficient leads to nonlinear anisotropic diffusion. The anisotropy causes the tangential component of the diffusion coefficient to remove noise around the object edges, while minimizing the diffusion normal to the object boundaries. The diffusion tensor calculation takes into account local features such as the gradient in the grayscale values and directionality of the gradients in the form of eigenvalues and eigenvectors. These local features are calculated using the structural tensor smoothed using the Gaussian filter of width σ. The eigenvector ei,j orients the co-ordinates along the local image structure and the relative magnitude of the eigenvalues λi can be used to identify the nature of the feature in the image such as corners, edges, planes and isolated noise voxels. Refer to Spies et al. (Scharr, and Spies, 2005 and Spies, Jahne, and Barron, 2002) for more details on the eigenvalue analysis.
[1] ![]()
[2] 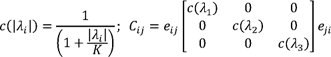
An edge stopping parameter (K) is used to distinguish the noise present in the homogenous region of the image from the edges. This information is difficult to obtain by visual observation of the image histogram. Eigenvalue analysis shows that the smallest eigenvalue averaged over the whole image is a good measure of the uncorrelated noise in the image (Spies, Jahne, and Barron, 2002). Since equation [1] is solved iteratively and there is no definite measure of the enhancement of the image, a pre-defined stopping criterion does not exist for the diffusion application on an image. Here, we use the initial measure of the image noise as the starting point and the iterative process is stopped when the confidence level (Scharr, and Spies, 2005) reaches the pre-specified value of 0.75.
3. Indicator kriging
Kriging (Rossi, Dungan, and Beck, 1994) is a commonly used geo-statistics technique to estimate a value at an un-sampled location based on measured values in the neighborhood locations. However from an image segmentation point of view, the probability of the unknown having a value larger than the threshold is more useful. Indicator kriging provides this probability using linear-weighted combinations of the measured values in the neighborhood. Oh and Lindquist (Oh, and Lindquist, 1999) describe an indicator kriging technique for image thresholding in conjunction with the two point spatial covariance. The algorithm is implemented in two steps: (1) The thresholding step involves a priori assignment of a portion of the image voxels into two populations; and (2) the kriging step where the kriging weights are calculated from the two point spatial covariance relation calculated using smoothed indicators. The linear combinations of weights and indicators are then used to calculate the probability of the unknown voxel belonging to either population. The two sets of weights are calculated from the globally averaged covariance relations for each assigned population and hence the weights are globally averaged and need to be calculated only once. Information on balancing of the negative weights and how to treat the voxels near the image boundaries can be found in the original paper (Oh, and Lindquist, 1999). Their algorithm also uses two passes of a majority filter to remove the isolated voxels in the a priori assigned population. In our implementation we do not follow this approach since we have found that it introduces artifacts such as joining of separated particles and loss of thin features from the segmented image.
4. Results and discussion
Here, we will demonstrate our methods on a three phase image of size 350*350*350 voxels3 (with a voxel resolution of 9.92 µm) that contains quartz sand (solid), a chlorinated solvent (tetrachloroethylene) as oil phase and water that was doped with 8% KI. The imaging was performed at X-ray energies below (33.07 keV, Figure 1a) and above (33.27 keV, Figure 1b) the iodine absorption k- edge. Visual observation of the below edge image (Figure 1a) show three distinct phases. However, in the image histogram (Figure 1c), the peaks for the oil and water phases are merged due to similarity in absorbance at this energy and large variance in the phase gray scale values. This makes the below-edge image ideal for our study. The above-edge image will be used for comparison of the final segmentation results. The below-edge image was first subjected to the nonlinear anisotropic diffusion process to remove noise from the image. Visual inspection of Figures 2a-2b shows that there is over smoothing of the image at higher user-specified values of K resulting in blurring, while the lower values of K results in lower diffusive flux and require higher numbers of iterations to achieve satisfactory noise removal. The selection of the appropriate K values (faster noise removal while still preserving the features) is an important consideration. After the application of anisotropic diffusion, the image can be segmented using threshold-based techniques. The impact of noise removal on image segmentation can be seen in Figure 3. Simple thresholding of the original image (Figure 3a) shows a significantly larger number of noise voxels than the image that was processed with the nonlinear anisotropic noise removal algorithm. This negates the need to employ post-segmentation noise removal schemes such as the majority filter.
Figure 1. Section of the image acquired at two energies above and below the iodine absorption K edge. (a) Below edge image at energy 33.07keV, (b) above edge image at energy 33.27keV, (c) histogram of the below edge image. All images are of size 350*350*350

Figure 2. Section of the image showing the effect of edge stopping parameter (K) using EED filter. (a) K=10 after 10 iterations; (b) K=50 after 10 iterations and (c) K selected automatically using the average of the lowest eigenvalue, and stopping criteria 0.75 was also applied. Results achieved in 3 iterations and (d) histogram showing peak separation.
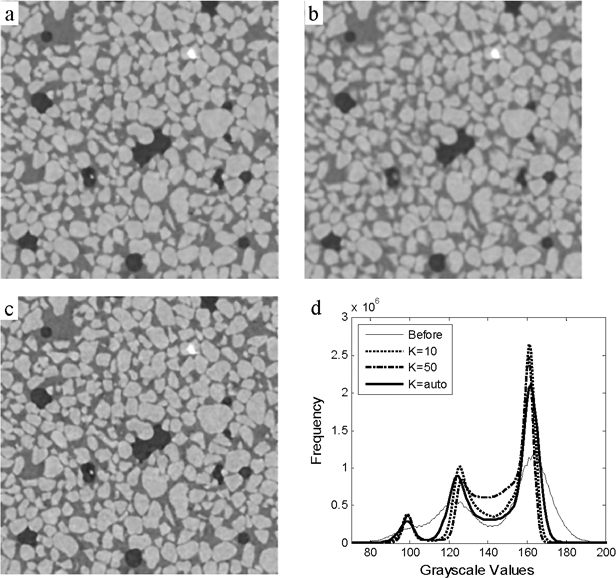
Figure 3. Section of the image showing the results of simple thresholding test: (a) simple threshold results showing misclassified voxels in the original image; (b) simple threshold results showing the smoothing of noise voxels using anisotropic diffusion

From the histogram of the filtered image (Figure 2d) we can see that there is a range of values between two peaks, and in the filtered image these values lie mostly at the phase boundaries. Hence a single threshold value cannot be used for the segmentation of phases.
Here, we use an indicator kriging-based algorithm, which uses two threshold values for the partial segmentation of the image into two phases and grayscale values between the two thresholds are assigned to either of the phases using the kriging statistics. Indicator kriging is designed mainly for data with two univariate peaks (e.g. two phases in a grayscale image). In our segmentation scheme for the three-phase-image, we choose to first segment the phase that results in a smaller standard deviation on either side of the chosen threshold values. For example, thresholding the solid phase (the far right peak in Figure 2d) results in a maximum standard deviation of 11.98 in the a priori assigned voxels and the segmentation of the oil phase (the far left peak in Figure 2d) results in a maximum standard deviation of 16.78.
Thus, we segment the solid phase on the first pass (Figure 4c). In the second pass, the segmented image is subtracted from the clean gray scale image so that the range of grayscale values in the image represents only the two fluid phases (Figure 4d). During the next step, the segmented solid phase is not used to calculate the two point covariance correlation, and during the probability calculation, the segmented part is treated as the boundary with an indicator value of 0.5. The resulting segmented image (Figure 4e) contains all three phases: oil, water and solids.
Figure 4. Section of the image showing the Indicator Kriging segmentation for 3 phase image. (a) Noise free below-edge image, (b)Partially thresholded image: White-solid, Black-Rest of the image containing Oil and Water, Gray-Unassigned voxels, (c) Segmented image showing solid (White) and rest of the image (Black), (d) Solid subtracted from the clean grayscale image, (e) Fully segmented three phase image using below edge image only white-Solid (57.508%), Gray-Water (35.436%) and Black-Oil phase (7.056%) and (ƒ)Fully segmented three phase image using both above and below edge images, white-Solid (57.508%), Gray-Water (35.395%) and Black-Oil phase (7.097%).
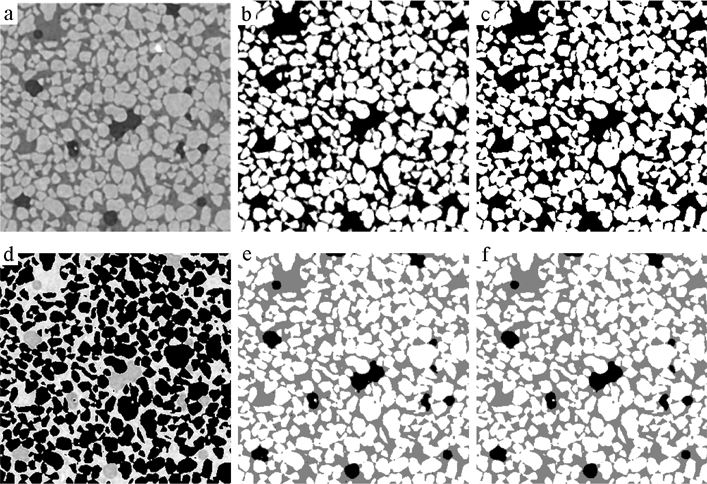
Following the method described above, the above-edge image is also subjected to nonlinear anisotropic diffusion (with the same parameters) and the indicator kriging program is used for segmentation of the oil phase from the rest of the image. The solid phase segmentation from the below edge image is the same as shown in Figure 4c. The solid-segmented image is combined with the oil-segmented image to obtain a three-phase image (Figure 4f). Comparison of the two images (Figures 4e and 4f) shows a nearly identical segmentation.
5. Conclusion
Nonlinear anisotropic diffusion, aided by automatic eigenvalue analysis of the edge stopping parameter, effectively removes noise from porous media images while preserving the local structure in the data and not blurring the edges. The peak separation and reduction in the grayscale variance of each peak increases the accuracy of the image segmentation. Comparison of the segmentation of a single image segmented to separate three phases with a segmented image obtained from above- and below-edge images show that this approach is effective and should prove useful for separating phases in XCT images where absorption edge imaging is not an option.
6. Acknowledgements
The authors acknowledge Keegan L. Roberts, Civil and Environmental Engineering, Louisiana State University (LSU) for providing us with the XCT images. The images were collected at GeoSoilEnviroCARS (Sector 13), Advanced Photon Source (APS), Argonne National Laboratory. GeoSoilEnviroCARS is supported by the National Science Foundation - Earth Sciences (EAR-0622171) and Department of Energy - Geosciences (DE-FG02-94ER14466). Use of the Advanced Photon Source was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. The authors acknowledge the members of the PoreSim Research Consortium at LSU (BP America, Millipore, Schlumberger) for financial support.
7. References
Sheppard, A.P., R.M. Sok, and H. Averdunk, “Techniques for image enhancement and segmentation of tomographic images of porous materials”, Physica A, 2004, 339, 145-151.
Vincent, L. and P. Soille, “Watersheds in digital spaces: an efficient algorithm based on immersion simulations”, IEEE Trans. Pattern. Anal. Machine Intell., 1991, 13, 583-598.
Herman, G.T., “On the noise in images produced by computed tomography”, Computer Graphics and Image Processing, 1980, 12, 271-285.
Perona, P. and J. Malik, “Scale-space and edge detection using anisotropic diffusion”, IEEE Trans. Pattern Anal. Machine Intell., 1990, 12, 629-639.
Scharr, H. and H. Spies, “Accurate optical flow in noisy image sequences using flow adapted anisotropic diffusion”, Signal Process.Image Comm., 2005, 20, 537-553.
Spies, H., B. Jahne, and J.L. Barron, Range flow estimation, Computer Vision and Image Understanding, 2002, 85, 209-231.
Rossi, R.E., J.L. Dungan, and L.R. Beck, Kriging in the Shadows - Geostatistical Interpolation for Remote-Sensing, Remote Sensing of Environment, 1994, 49, 32-40.
Oh, W. and W.B. Lindquist, Image thresholding by indicator kriging, IEEE Trans. Pattern Anal. Machine Intell., 1999, 21, 590-602.
