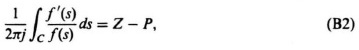APPENDIX B
PROOF OF THE NYQUIST
STABILITY CRITERION
The Nyquist stability criterion can be derived from Cauchy’s residue theorem, which states that
Let us replace g(s) by f′(s)/f(s), where f(s) is a function of s which is single valued on and within the closed contour C and analytic on C. Observe that the singularities f′(s)/f(s) occur only at the zeros and poles of f(s). The residue may be found at each singularity with multiplicity of the order of zeros and poles taken into account. The residues in the zeros of f(s) are positive and the residues in the poles of f(s) are negative. Therefore, if f(s) is not equal to zero along C, and if there are not at most a finite number of singular points that are all poles within the contour C, then
where Z = number of zeros of f(s) within C, with due regrd for their multiplicity of order, and P = number of poles of f(s) within C, with due regard for their multiplicity of order. The left-hand side of Eq. (B2) may be written as
In general, f(s) will have both real and imaginary parts along the contour C. Therefore, its logarithm can be written as
If we assume that f(s) is not zero anywhere on the contour C, the integration of Eq. (B3) results in the expression
where, s1 and s2 denote the arbitrary beginning and end of the closed contour C as it is followed. Because |f(s)| returns to its initial value in completing the closed curve,
Therefore, Eq. (B6) can be rewritten as
By equating Eqs. (B2) and (B7), we obtain
Equation (B8) states that the excess of zeros over poles of f(s) within the contour C equals 1/2π times the net change in angle (i.e., equals the number of net encirclements of the origin) of f(s) as s is varied over the contour C. Let N be this number. Then Eq. (B8) can be written as
where the contour C is traversed in a clockwise direction, and where an encirclement is defined as being positive if it also is in a clockwise direction. The number Z must be zero for the system to be stable.
This relationship, which is known as Cauchy's principle of the argument, is the basis of Nyquist's stability criterion. To make use of this principle in applying Nyquist's stability criterion, let us consider the feedback control system of Figure B1. Let
![]()
and examine the number of times f(s) encircles the origin as s traverses the contour of Figure B2. (It is assumed that there are no poles on the imaginary axis, except at the origin.) Observe that the origin of f(s) corresponds to G(s)H(s) = −1. Therefore, if G(s)H(s) is plotted for the contour of Figure B2, the number of times that G(s)H(s) encircles the point −1 + j0 equals the number of zeros minus the number of poles of 1 + G(s)H(s) for s in the right half-plane.

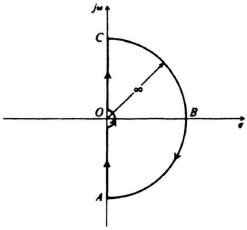
Let us examine the contour of Figure B2 in detail. Because
for all physical systems, the points along the infinite arc ABC contract to the origin for ω = 0. Along the small semicircle about the origin, let
Because G(s)H(s) is usually a rational function with a denominator of higher power than that of the numerator, then
will map into a segment of an infinite circle. Along the imaginary axis, s = jω, so that we are concerned with G(jω)H(jω). Because G(−jω)H(−jω) is a conjugate of G(jω)H(jω), the two functions are symmetric about the real axis and G(−jω)H(−jω) is a reflection of G(jω)H(jω) about the real axis. Therefore, it is only necessary to plot G(jω)H(jω) from ω = 0 to ∞.
Therefore, N can be determined by plotting G(jω)H(jω) and observing the number of encirclements of the −1 + j0 point; P can be determined by inspection of the G(s)H(s) expression; and Z can be found by using Eq. (B9).