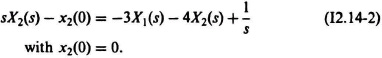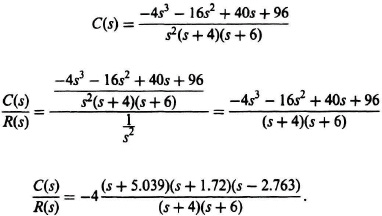2.30  ILLUSTRATIVE PROBLEMS AND SOLUTIONS

This section provides a set of illustrative problems and their solutions to supplement the material presented in Chapter 2.

I2.1. Determine the poles and zeros of

SOLUTION: Simple poles are located at s = 0, −2, −6

Pole of order two located at −8

Simple zeros located at −1, −4

I2.2. Determine the Laplace transform of f(t) which is given by

f(t) = te^4t,   t ≥0

f(t) = 0,      t > 0.

SOLUTION: From Appendix A, eighth item: For n = 2 and a = −4, we obtain

I2.3. Determine the Laplace transform F(s) for the function f(t) illustrated:

Figure I2.3

SOLUTION:

f(t) = 2U(t) − 4U(t − 1) + 2U(t − 2)

From Table 2.1, item 2, and the time-shifting theorem, we obtain

I2.4. Determine the initial value of c(t) where the Laplace transform of C(s) is given by:

SOLUTION: From the initial-value theorem

we obtain,

I2.5. Determine the final value of c(t) when the Laplace transform of C(s) is given by

SOLUTION: From the final-value theorem

we obtain,

I2.6. Determine the final value of c(t) when the Laplace transform of C(s) is given by

SOLUTION: The final-value theorem cannot be applied in this problem because the function sC(s) is not analytic in the right half-plane.

I2.7. Determine the Laplace transform of

c(t) = sin ωt U(t − 2)

from knowledge of the Laplace transform of a sine wave (see Table 2.1, item 7) and the time-shifting theorem.

SOLUTION:

I2.8. Determine the Laplace transform of

c(t) = e^−3t sin ωt U(t)

from knowledge of the Laplace transform of a sine wave (see Table 2.1, item 7) and the frequency-shifting theorem.

SOLUTION:

I2.9. Determine the Laplace transform of the function f(t) where

f(t) = e^−t(t−1)U(t − 1).

SOLUTION:

To integrate this equation, it is necessary to change the variable as follows:

  Let τ = t − 1.

Therefore,

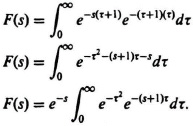
Adding the term

e^0.52 e^(s+1)2

inside and outside the integral to complete the square, we obtain the following:

Let us now change the variable. By defining the new variable T as follows:

T = τ + 0.5(s + 1).

Therefore,

The integral term is equal to:

0.5π^0.5(1 − error function)

Abbreviating the error function as “erf,” the Laplace transform is given by the following:

F(s) = 0.5π^0.5e^0.52(s−1)2(1 − erf(0.5)(s + 1)).

I2.10. Determine the residues of F(s) where

which has single poles at s = −2 and s = −4.

SOLUTION: The residue at s = −2 is given by

The residue at s = −4 is given by

I2.11. Determine the inverse Laplace transform of C(s) where

SOLUTION: Using partial-fraction expansion, we obtain the following:

where

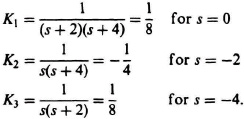
From Table 2.1, items 2 and 6 we obtain the following:

I2.12. Determine the inverse Laplace transform of C(s) where

SOLUTION: Using partial-fraction expansion, we obtain the following:

where

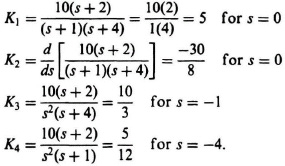
From Table 2.1, items 2, 3, and 6, we obtain the following:

I2.13. Determine the value of c(t) for the following differential equation using the Laplace transform. Assume that the initial conditions are zero, and U(t) represents a unit step.

SOLUTION:

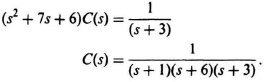
Using partial-fraction expansion, we obtain the following:

where

Therefore,

c(t) = (0.1e^−t + 0.067e^−6t − 0.167e^−3t)U(t).

I2.14. Solve the following two differential equations for x₁(t) and x₂(t) by means of the Laplace transform.

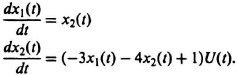
The initial conditions are: x₁(0) = 1; x₂(0) = 0.

SOLUTION:

Therefore,

sX₁(s) − 1 = X_s(s).

Solving for X₁(s):

Substituting X₁(s) from Eq. (I2.14-3) into Eq. (I2.14-2), we obtain:

Using partial-fraction expansion, we obtain:

where

Therefore,

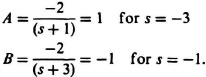
Taking the inverse Laplace transform of X₂(s), we obtain

x₂(t) = (e^−3t − e^−t)U(t).

Substituting Eq. (I2.14-4) into Eq. (I2.14-1), we obtain

Solving for X₁(s), we obtain the following:

Using partial-fraction expansion, we obtain:

where

Therefore,

Taking the inverse Laplace transform of X₁(s), we obtain

x₁(t) = (0.33 − 0.33e^−3t + e^−t)U(t)

I2.15. Determine the value of c(t) for the following differential equation using the Laplace transform.

where

r(t) = e^−3tU(t).

SOLUTION: Since

then

Taking the Laplace transform of this equation, we obtain the following:

Solving for C(s), we obtain the following:

Using partial-fraction expansion, we obtain the following:

where

Therefore,

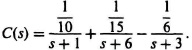
Taking the inverse Laplace transform of this equation, we obtain

I2.16. A unit impulse is applied to an element whose transfer function is unknown. If the resulting output is given by

c(t) = 4e^−6tU(t)

where U(t) represents a unit step, determine the transfer function of the element.

SOLUTION: Since

and

R(s) = 1

Therefore,

I2.17. A system is represented by the following differential equation:

In this differential equation, r(t) represents the input, and c(t) represents the output. Determine the transfer function C(s)/R(s).

SOLUTION: Taking the Laplace transform of this differential equation, we obtain the following:

C(s)(4s² + 3s + 6) = R(s) + 4R(s)e^−s.

Therefore, the transfer function C(s)/R(s) is given by

I2.18. A system is represented by the following differential equation:

In this differential equation, r(t) represents the input, and c(t) represents the output. Determine the transfer function C(s)/R(s).

SOLUTION:

Taking the Laplace transform of this differential equation, we obtain the following:

Simplifying this equation, we obtain the following:

C(s)(s⁴ + 10s³ + 6s² + s + 7) = s²R(s) + 3sR(s).

Therefore, the transfer function C(s)/R(s) is given by

I2.19. We wish to determine the transfer function of an element in a control system. To determine its transfer function, a unit ramp is applied to the input r(t). The output of this element is recorded, and is modelled according to the following equation:

c(t) = (4t − 2e^−4t − 2e^−6t)U(t).

Determine the transfer function, C(s)/R(s), of this element.

SOLUTION: Since

and

simplifying the expression for C(s) results in the following:

I2.20. We wish to determine the transfer function of an element in a control system. Its input, m(t), represents speed, and its output is represented by y(t). To determine its transfer function, a unit step voltage of 1 volt, corresponding to a speed of 1 ft/sec, is applied to the input, m(t). The output of the element is recorded and is modeled according to the following equation:

y(t) = (40 − 8e^−5(t−1))U(t − 1)

Determine the transfer function, Y(s)/M(s), of this element. Reduce your answer to its simplest form.

SOLUTION: The Laplace transform of the output y(t) is given by

Simplifying the expression for Y(s) results in the following:

Therefore, the transfer function Y(s)/M(s) is given by

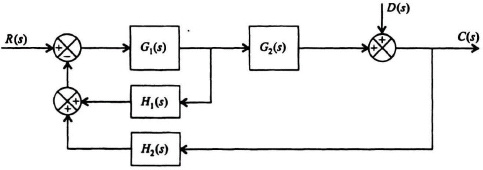
I2.21. The block diagram of a control system is illustrated where R(s) represents the reference input and D(s) represents the disturbance input.

(a)  Determine the transfer function C(s)/R(s).

(b)  Determine the transfer function C(s)/D(s).

(c)  Determine the value of the feedback element H₁(s) in order that the disturbance input D(s) has no effect on the output C(s). Assume that R(s) = 0.

Figure I2.21

SOLUTION: (a)          

(b)                    

(c)  Setting the numerator of the transfer function C(s)/D(s) = 0, we obtain the following:

1 + G₁(s)H₁(s) = 0.

Therefore,

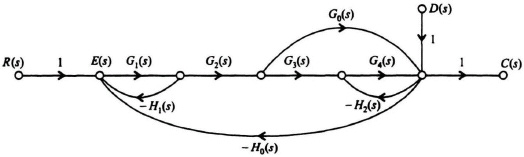
I2.22. The signal-flow graph of a control system is represented by the following, where D(s) represents an external disturbance input into the control system:

(a)  Determine the transfer function C(s)/R(s).

(b)  Determine the transfer function E(s)/D(s).

Figure I2.22

SOLUTION: (a)

All terms in this transfer function are functions of s.

(b)

I2.23. Consider the LC ladder network illustrated:

Figure I2.23(I)

The circuit equations representing this LC network are as follows:

(a)  Draw the signal-flow graph representing these circuit equations.

(b)  Using Mason’s theorem, determine the transfer function, V_out(s)/V_in(s).

SOLUTION: (a)

Figure I2.23(II)

(b)               

I2.24. A feedback control system is represented by the following signal-flow graph:

Figure I2.24

Determine the phase-variable canonical form equations for this feedback control system.

SOLUTION: The differential equations representing this signal-flow graph are given by the following:

₁(t) = −ex₁(t) + x₂(t) + ar(t)

₂(t) = −cx₁(t) − dx₂(t) + r(t).

The phase-variable canonical equations are given by:

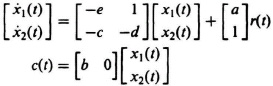
I2.25. Determine the state transition matrix as a sum of an infinite series using Eq. (2.323) for a system whose P matrix is given by:

Carry out the computation in Eq. (2.323) from k = 0 through k = 2.

SOLUTION:

I2.26. A system has a companion matrix, P, and an input vector, B, given by the following:

(a)  Determine its state transition matrix using Eq. (2.256).

(b)  Solve the state transition equation, Eq. (2.306), for t ≥ 0. Assume that the input is a unit step function, and that the initial state vector is represented by x(0) where

SOLUTION: (a) From Eq. (2.256):

Φ(t) = ℒ⁻¹{[sI − P]⁻¹}, for t 0

where

and

Therefore,

(b)  From Eq. (2.306):

where

This reduces to:

Therefore,

I2.27. Using the elements presented in Section 2.18 on Operational Amplifiers, develop a flow diagram to simulate the following set of differential equations which represent the model of a system. The outputs from the system are the variables x(t) and y(t).

Assume the initial conditions are zero.

SOLUTION:

Figure I2.27