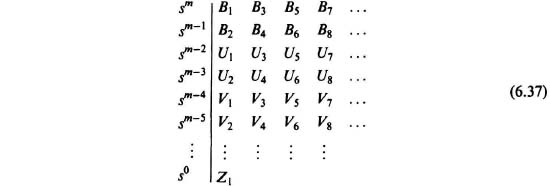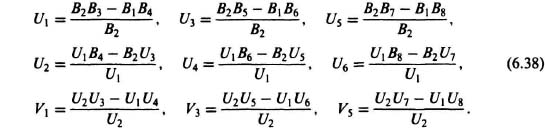6.3.  ROUTH—HURWITZ STABILITY CRITERION

The Routh–Hurwitz stability criterion is an algebraic procedure for determining whether a polynomial has any zeros in the right half-plane. It involves examining the signs and magnitudes of the coefficients of the characteristic equation without actually having to determine its roots. This method does not indicate the relative degree of stability or instability.

Routh [3] and Hurwitz [4] independently determined the necessary and sufficient conditions for stability from the signs and magnitudes of the coefficients of the characteristic equation. A useful form of their approach is described below.

Let us represent the general form of the characteristic equation by

If a coefficient is negative or zero when at least one of the other coefficients is positive, then a root exists which is in the right half-plane or is imaginary. For this case, the system is unstable and one can stop here. If all the coefficients are present, real, and positive, then the coefficients are arranged in two rows:

We obtain additional rows of coefficients from these two rows as follows:

where

This pattern will continue until all the terms in a row are zero. The rows are indexed downwards, the first row being numbered m, the degree of the original polynomial; the last row being numbered 0. The number of rows obtained will be m + 1, where m is the order of the characteristic equation. Note that there is one exceptional case where this will not be so; this is discussed later on. The criterion of stability is to check that all the terms in the left-hand column (B₁, B₂, U₁, U₂, V₁, V₂, …) have the same sign. If so, there are no roots in the right half-plane. If there are X changes of sign, then X roots exist in the right half-plane.

Let us illustrate the approach with a simple example. Consider the characteristic equation

Using the procedure described, the resulting array is

There are two changes of sign in the first column: 4 to −25 and −25 to 500; therefore, there are two roots in the right half-plane, and the system is unstable.

If the first term in any row is zero, and the other terms of the row are not zero, the array of Eq. (6.37) may be continued by replacing the first column zero by an arbitrary small positive constant . The process is then continued in the usual manner. Let us illustrate the procedure for this particular case with a simple example. Consider the following characteristic equation:

Using the procedure described, the resulting array is

As approaches zero, the limiting value of the term in the left-hand column, fourth row, is negative. The limiting value of the term in the left-hand column, fifth row, is positive. Therefore there are two changes of sign, two roots must lie in the right half-plane, and the system is unstable.

The exceptional case referred to above occurs when all the terms in a row are zero before the (m + l)th row is reached. This means that there are pairs of real roots existing that are negatives of each other located on the real axis, pairs of conjugate roots on the imaginary axis, or quadruples of roots symmetrically located with respect to the origin. For this special case, the array of Eq. (6.37) can be completed by obtaining a subsidiary polynomial from the preceding row. The subsidiary polynomial equation is formed by constructing a polynomial whose coefficients are the coefficients of the last nonzero row. To determine the degree of the subsidiary polynomial, the rows are indexed downwards, the first row being numbered m, the degree of the original polynomial. Then the index of the last nonzero row is the degree of the subsidiary polynomial. This polynomial, which is always even, is then differentiated and the resulting coefficients are used to complete the array. The zeros of the subsidiary polynomial are actual roots of the characteristic equation. This procedure is illustrated with a simple example. Consider the following characteristic equation:

Using the procedure described, the resulting array is

The presence of zeros in the third row indicates the exceptional case. Using the coefficients of the second row for the subsidiary equation, we obtain

In order to complete the array, Eq. (6.45) is differentiated and the resulting coefficients are then inserted into the array as follows:

No roots lie in the right half-plane because there are no changes of sign in the left-hand column. The roots that are negatives of each other can be obtained from Eq. (6.45) as ±j4, indicating a pair of imaginary roots. Although the Routh–Hurwitz criterion does not consider such a system to be unstable (because its roots do not lie in the right half plane), it is unstable from practical control considerations.

As a concluding example of the application of the Routh–Hurwitz criterion, let us determine the maximum value of gain K that a feedback system could have before the system becomes unstable. Another way of looking at this is to find K where the roots exist on the imaginary axis. Consider a system whose open-loop transfer function is given by

Its characteristic equation is given by

The resulting Routh–Hurwitz criterion is given by

By setting the term U₁ equal to zero, we find that the maximum value of K before the system becomes unstable is given by

or

If K > 2, then there are two sign changes in the first column, indicating two roots in the right half-plane, and the system is unstable.

Although the Routh–Hurwitz criterion gives a relatively quick determination of absolute stability, it does not show how to improve the design. In addition, it does not give an indication of relative system performance. Its main attribute is to serve as a check of other design criteria. The greatest difficulty with using the Routh–Hurwitz criterion, however, is that it assumes that the characteristic polynomial is known.