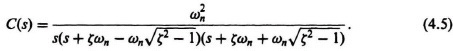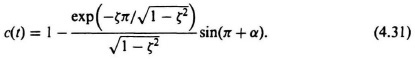4.2.  CHARACTERISTIC RESPONSES OF SECOND-ORDER CONTROL SYSTEMS

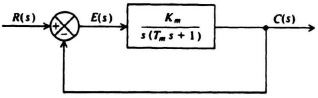
The purpose of this section is to describe the transient response of a typical feedback control system. We consider a very common configuratuon in which a two-phase ac servomotor, whose transfer function is given by Eq. (3.101) is enclosed by a simple unity feedback loop. Figure 4.1 illustrates the block diagram of this second-order system. For purposes of simplicity, the gain of the amplifier driving the motor is assumed to be unity.

The closed-loop transfer function of this system is given by

By defining the undamped natural frequency ω_n and the dimensionless damping ratio ζ as

Eq. (4.1) can be rewritten as

The parameters ω_n and ζ are very important for characterizing a system’s response. Note from Eq. (4.3) that ω_n turns out to be the radian frequency of oscillation when ζ = 0. As ζ increases from 0, the oscillation decays exponentially and becomes more damped. When ζ 1, an oscillation does not occur.

We assume that the initial conditions are zero and the input is a unit step. Therefore, R(s) = 1/s, and the Laplace transform of the output can be written as

Factoring the denominator, we obtain

The exact solution for the output in the time domain is dependent on the value of ζ. When ζ 1, the second-order system has poles which lie along the negative real axis of the complex plane. When ζ < 1, however, a pair of complex-conjugate poles result. We shall determine the output response to a step input for the three cases: where the damping ratio equals unity, is greater than unity, and is less than unity.

Figure 4.1   Second-order feedback system containing a two-phase ac servomotor.

Case A.  Damping Ratio Equals Unity

When ζ = 1, Eq. (4.5) reduces to

The time-domain response can be obtained by utilizing the solution obtained for Eq. (2.82). The partial-fraction expansion of Eq. (4.6) is given by

Using Eqs. (2.85), (2.87), and (2.88) with A = D = 0, B = C = ω_n, we find that

Substituting these constants into Eq. (4.7), we obtain

The time-domain response of the output, c(t), may be obtained by utilizing the table of Laplace transforms given in Appendix A:

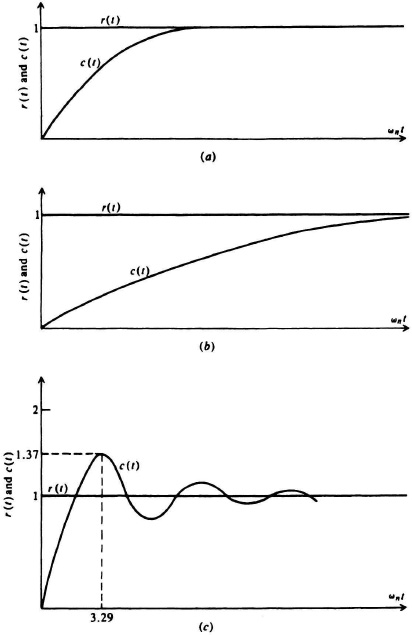
Figure 4.2a illustrates the output response together with the unit step input. Notice that the output response exhibits no overshoots when ζ = 1. The response is described as being critically damped.

Case B.  Damping Ratio Greater than Unity

When ζ > 1, the time-domain response can be obtained quite simply from its partial fraction expansion. This can be expressed as

where ζω_n − ω_n and ζω_n + ω_n are positive real numbers.

The constants K₁, K₂, and K₃ can be evaluated quite simply by the methods described in Chapter 2. Their values are

Figure 4.2   (a) Input and output response for a critically damped second-order system; (b) input and output response for an overdamped second-order system; (c) input and output response for an under-damped second-order system (ζ = 0.3).

Therefore Eq. (4.13) can be written as

The time-domain response of the output, c(t), may be obtained by utilizing the table of Laplace transforms given in Appendix A. It can be expressed as

Figure 4.2b illustrates the output response together with the unit step input. Notice that when ζ > 1, the output response exhibits no overshoots and takes longer to reach its final value than when ζ = 1. This response is described as bieng overdamped.

Case C.  Damping Ratio Less than Unity

When ζ < 1, the time-domain response can be obained in an analogous manner. The solution is slightly more complex, however, because we now have a pair of complex-conjugate poles. The partial fraction expansion of Eq. (4.5) can be written as

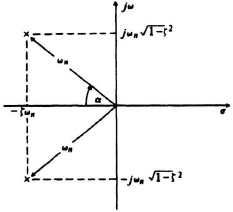
The constants K₁, K₂, and K₃ can be evaluated in an analogous manner by the method described in Chapter 2, but the algebra becomes a little complicated. In order to simplify this situation somewhat, use is made of the relationship between the location of the complex-conjugate poles in the complex plane and the damping ratio ζ. The geometry of the configuration is illustrated in Figure 4.3. Notice that the distance from the origin to either pole equals ω_n. In addition, the angle α has the following trigonometric properties:

Figure 4.3   Location of the complex-conjugate poles in the complex plane.

Utilizing the relations given by Eqs. (4.18) and (4.19), the constants K₁, K₂ and K₃ can be expressed as

Therefore Eq. (4.17) can be written as

The time-domain response of the output, c(t), may be obtained by utilizing Appendix A. It can be expressed as

This can be simplified to

or

Figure 4.2c illustrates the output response for a value of ζ which has a value of 0.3, together with the unit step input. Notice that the output response exhibits several overshoots and undershoots before finally settling out. This response, which is characteristic of an exponentially damped sinusoid, is described as being underdamped.

Examination of Eq. (4.24) indicates that the term in the exponent, ζω, multiplies t and it controls the exponential decay or rise of the unit step response, c(t). Therefore, ζω_n determines the “damping” of the system and it is defined as the damping factor of the system. Note that the inverse of ζω_n is proportional to the time constant of the system.

Observe from Eq. (4.12) that when the system is critically damped and ζ = 1, the damping factor equals ω_n. Therefore, we view ζ as the damping ratio which is defined as follows:

The time to the first overshoot and the value of the first overshoot are two interesting identifying characteristics for this type of response. We shall next derive these values in terms of the undamped natural frequency ω_n and the damping ratio ζ.

Equation (4.24) indicates that the damped natural radian frequency of oscillation of the system, ω_m, is

The damped natural cyclic frequency of oscillation of the system, f_m, is

The period of oscillation of the underdamped system, t_m, is

The time at which the peak overshoot occurs, t_p, is found by differentiating c(t), from Eq. (4.24), with respect to time and setting the derivative equal to zero:

This derivative is zero when

The peak overshoot occurs at the first value after zero, provided there are zero initial conditions. Therefore, the time to the first peak, t_p, and ω_nt_p are given by

For the case illustrated in Figure 4.2c, where ζ = 0.3, the time to the first overshoot is 3.29/ω_n.

Substituting Eq. (4.30) into Eq. (4.24) yields the value for the maximum instantaneous value of the output, c(t):

This can be simplified by substituting

Therefore,

This is usually expressed as a percentage of the input. Therefore, for a unit step input,

For the case illustrated in Figure 4.2c, where ζ = 0.3, the maximum percent overshoot is 37%.

The second-order system is a very common and popular one. In order for the reader to become more familiar with its typical characteristic responses, Figures 4.4 and 4.5 are shown to illustrate the resulting transient responses and percent maximum overshoots, rexpectively, for several values of damping factor.

It is interesting to compare the sketches of Figure 4.2a, b, and c. The critically damped system appears to be a compromise among the three systems shown. Although it does take a longer time to reach the desired value of unity than the underdamped system, it does not exhibit overshoots. The underdamped system, however, oscillates several times around the desired value before it finally settles to its steady-state value. Depending on the value of the damping ratio, the under-damped system may reach its final value faster than the critically damped system. Overdamped systems are rarely used in practice. As a matter of interest, practical systems are usually designed to be somewhat underdamped. Section 4.5 will discuss the best damping ratio to use for different applications.