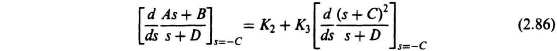2.7.  INVERSION BY PARTIAL FRACTION EXPANSION

The time response is the quantity of ultimate interest to the control-system designer. The process of inversion of a function F(s) to find the corresponding time function f(t) is denoted symbolically by

In applications, F(s) is usually a rational function of the form

In practical systems, the order of the polynomial in the denominator is equal to, or greater than, that of the numerator. For the cases where Y > X, partial fraction expansion is directly applicable. When Y X, it is necessary to reduce F(s) to a polynomial in s plus a remainder (ratio of polynomials in s).

The simplest method for obtaining inverse transformations is to use a table of transforms. Unfortunately, many forms of F(s) are not found in the usual table of Laplace-transform pairs. When the form of the solution cannot be readily reduced to a form available in a table, we must use the technique known as partial fraction expansion. This method permits the expansion of the algebraic equation into a series of simpler terms whose transforms are available from a table. It is then possible to obtain the inverse transformation of the original algebraic expression by adding together the inverse transformations of the terms in the expansion. Equation (2.75) expresses this operation symbolically. The function F(s) represents the original algebraic expression and F₁(s), F₂(s), F₃(s), . . ., F_n(s) are terms of the partial fraction expansion:

As an example of the method, consider the transform

In this equation A, B, C, and D are constants. This function can be expanded into partial fractions:

where K₁ and K₂ are the coefficients of the expansion, and the coefficients K_i are called the residues at the pole s = −p_i, The residues are determined by multiplying both sides of Eq. (2.79) by the denominator factor, (s + p_i), corresponding to K_i and setting s equal to its root, s = −p_i.

To determine K₁, both sides of Eq. (2.79) are multiplied by s + C, yielding

By substituting s = −C, the last term vanishes and a numerical value for K₁ can be obtained. An analogous procedure leads to the value for K₂. One finds

An expression for the expanded form of F(s) can now be obtained by substituting this result into Eq. (2.79):

It is now a simple process to obtain the inverse Laplace transform from this last equation. The corresponding time function can be obtained by inspecting the terms and comparing them with transform pairs listed in Table 2.1 or Appendix A:

Transforms with multiple poles are also encountered. For example, consider the transform

In this equation A, B, C, and D are constants. The partial fraction expansion is written as

To find K₁, both sides of Eq. (2.83) are multiplied by (s + C)²:

The constant K₁ can now be evaluated by simply substituting s = −C:

In order to determine the constant K₂, both sides of Eq. (2.84) must be differentiated with respect to s, and s is then set equal to −C:

The resulting numerical value for K₂ is given by

The constant K₃ can be obtained by the same procedure used in evaluating the expression given by Eq. (2.78). Its value is

The corresponding time function can be obtained by inspecting the terms in Eq. (2.83) and comparing them with the transform pairs listed in Table 2.1 or Appendix A: