9.5 Oblique Triangles, the Law of Sines

  • Oblique Triangles • Law of Sines • Case 1: Two Angles and One Side • Case 2: Two Sides and the Angle Opposite One of Them • Ambiguous Case

To this point, we have limited our study of triangle solution to right triangles. However, many triangles that require solution do not contain a right angle. Such triangles are called oblique triangles. We now discuss solutions of oblique triangles.

In Section 4.4, we stated that we need to know three parts, at least one of them a side, to solve a triangle. There are four possible such combinations of parts, and these combinations are as follows:

  • Case 1. Two angles and one side

  • Case 2. Two sides and the angle opposite one of them

  • Case 3. Two sides and the included angle

  • Case 4. Three sides

There are several ways in which oblique triangles may be solved, but we restrict our attention to the two most useful methods, the law of sines and the law of cosines. In this section, we discuss the law of sines and show that it may be used to solve Case 1 and Case 2.

Let ABC be an oblique triangle with sides a, b, and c opposite angles A, B, and C, respectively. By drawing a perpendicular h from B to side b, as shown in Fig. 9.51(a), note that h / c = sin A and h / a = sin C ,  and therefore

h= c sin Aor h= a sin C
(9.4)
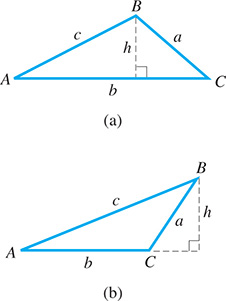
Two triangles.

Fig. 9.51

This relationship also holds if one of the angles is obtuse. By drawing a perpendicular h to the extension of side b, as shown in Fig. 9.51(b), we see that h / c = sin A . 

Also, in Fig. 9.51(b), h / a = sin(180 °  − C) ,  where 180 °  − C is also the reference angle for the obtuse angle C. For a second-quadrant reference angle 180 °  − C ,  we have sin[ 180 °  − (180 °  − C)]  = sin C .  Putting this all together, sin(180 °  − C) = sin C .  This means that

h= c sin Aor h= a sin( 180° − C) = a sin C
(9.5)

The results are precisely the same in Eqs. (9.4) and (9.5). Setting the results for h equal to each other, we have

c sin A= a sin C

Dividing each side by sin A sin C and reversing sides gives us

asin A= csin C
(9.6)

By dropping a perpendicular from A to a, we also derive the result

c sin B= b sin C

which, when each side is divided by sin B sin C, and reversing sides, gives us

bsin B= csin C
(9.7)

If we had dropped a perpendicular to either side a or side c, equations similar to Eqs. (9.6) and (9.7) would have resulted.

Next we combine Eqs. (9.6) and (9.7) into an important basic equation that allows us to solve oblique triangles for which the given information fits either Case 1 or Case 2.

Combining Eqs. (9.6) and (9.7), for any triangle with sides a, b, and c, opposite angles A, B, and C, respectively, such as the one shown in Fig. 9.52, we have the following:

Law of Sinesasin A = bsin B = csin C
(9.8)
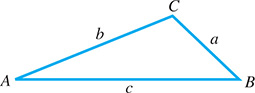
Triangle Ay B C with sides lower ay, lower b, and lower c.

Fig. 9.52

Another form of the law of sines can be obtained by equating the reciprocals of each of the fractions in Eq. (9.8). The law of sines is a statement of proportionality between the sides of a triangle and the sines of the angles opposite them. In finding the complete solution of a triangle, it may be necessary to use two of the three equations.

NOTE

[Note that there are actually three equations combined in Eq. (9.8). Of these, we use the one with three known parts of the triangle and we solve for the fourth part.]

CASE 1: TWO ANGLES AND ONE SIDE

Now, we see how the law of sines is used in the solution of a triangle in which two angles and one side are known. If two angles are known, the third may be found from the fact that the sum of the angles in a triangle is 180 °  .  Then, since the given side and its opposite angle are both known, we can use the law of sines (twice) to find each of the other two sides.

EXAMPLE 1 Case 1: Two angles and one side

Given c = 6.00 , A = 60.0 °  ,  and B = 40.0 °  ,  find a, b, and C.

First, we can see that

C = 180.0 °  − (60.0 °  + 40.0 ° ) = 80.0 ° 

We now know side c and angle C, which allows us to use Eq. (9.8). Therefore, using the equation relating a, A, c, and C, we have

Relating two equations.

Now, using the equation relating b, B, c, and C, we have

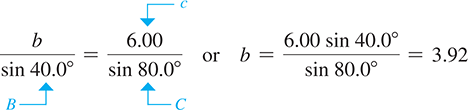
Relating two equations.

Thus, a = 5.28 , b = 3.92 ,  and C = 80.0 °  .  See Fig. 9.53. We could also have used the form of Eq. (9.8) relating a, A, b, and B in order to find b, but any error in calculating a would make b in error as well.

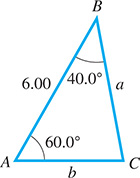
Triangle Ay B C where upper Ay = 60.0 degrees, upper B = 40.0 degrees, and side c = 6.00.

Fig. 9.53

NOTE

[The solution of a triangle can be checked approximately by noting that the smallest angle is opposite the shortest side, and the largest angle is opposite the longest side.]

Note that this is the case in Example 1, where b (shortest side) is opposite B (smallest angle), and c (longest side) is opposite C (largest angle).

EXAMPLE 2 Case 1: Two angles and one side

Solve the triangle with the following given parts: a = 63.71 , A = 56.29 °  ,  and B = 97.06 °  .  See Fig. 9.54.

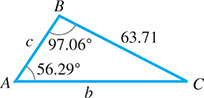
Triangle Ay B C where angle Ay = 56.29 degrees, angle B = 97.06 degrees, and side ay = 63.71.

Fig. 9.54

From the figure, we see that we are to find angle C and sides b and c. We first determine angle C:

C = 180 °  − (A + B) = 180 °  − (56.29 °  + 97.06 ° ) = 26.65 ° 

Noting the three angles, we know that c is the shortest side (C is the smallest angle) and b is the longest side (B is the largest angle). This means that the length of a is between c and b, or c < 63.71 and b > 63.71. Now using the ratio a/sin A of Eq. (9.8) (the law of sines) to find sides b and c, we have

Two set of relating equations.

Thus, b = 76.01 , c = 34.35 ,  and C = 26.65 °  .  Note that c < a and b > a ,  as expected.

If the given information is appropriate, the law of sines may be used to solve applied problems. The following example illustrates the use of the law of sines in such a problem.

EXAMPLE 3 Case 1—distance to helicopter

Two observers A and B sight a helicopter due east. The observers are 3540 ft apart, and the angles of elevation they each measure to the helicopter are 32.0 °  and 44.0 °  ,  respectively. How far is observer A from the helicopter? See Fig. 9.55.

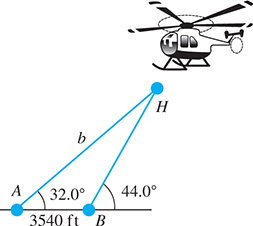
Triangle Ay B H with observers at Ay and B, and a helicopter at H. Angle Ay = 32.0 degrees, exterior angle B = 44.0 degrees, and side h = 3,540 feet. From Ay to H is side b.

Fig. 9.55

Letting H represent the position of the helicopter, we see that angle B within the triangle ABH is 180 °  − 44.0 °  = 136.0 °  .  This means that the angle at H within the triangle is

H = 180 °  − (32.0 °  + 136.0 ° ) = 12.0 ° 

Now, using the law of sines to find required side b, we have

An equation: b over sine of 136.0 degrees = 3,540 over sine of 12.0 degrees: b is the required side, and 3,540 is the known side. The denominators are the opposite known angles for their numerators.

or

b = 3540 sin 136.0 ° sin 12.0 °  = 11 , 800 ft

Thus, observer A is about 11,800 ft from the helicopter.

CASE 2: TWO SIDES AND THE ANGLE OPPOSITE ONE OF THEM

For a triangle in which we know two sides and the angle opposite one of the given sides, the solution will be either one triangle, or two triangles, or even possibly no triangle. The following examples illustrate how each of these results is possible.

EXAMPLE 4 Case 2: Two sides and angle opposite

Solve the triangle with the following given parts: a = 40.0 , b = 60.0 ,  and A = 30.0 °  . 

First, make a good scale drawing [Fig. 9.56(a)] by drawing angle A and measuring off 60 for b. This will more clearly show that side a = 40.0 will intersect side c at either position B or B ′  .  This means there are two triangles that satisfy the given values. Using the law of sines, we solve the case for which B is an acute angle:

60.0sin B = 40.0sin 30.0 ° orsin B = 60.0 sin 30.0 ° 40.0B = sin − 1(60.0 sin 30.0 ° 40.0) = 48.6 ° C = 180 °  − (30.0 °  + 48.6 ° ) = 101.4 ° 

Therefore, B = 48.6 °  and C = 101.4 °  .  Using the law of sines again to find c, we have

csin 101.4 °  = 40.0sin 30.0 ° c = 40.0 sin 101.4 ° sin 30.0 °  = 78.4

Thus, B = 48.6 °  , C = 101.4 °  ,  and c = 78.4. See Fig. 9.56(b).

Three figures.

Fig. 9.56

The other solution is the case in which B ′  ,  opposite side b, is an obtuse angle. Therefore,

B ′  = 180 °  − B = 180 °  − 48.6 °  = 131.4 ° C ′  = 180 °  − (30.0 °  + 131.4 ° ) = 18.6 ° 

Using the law of sines to find c ′  ,  we have

c ′ sin 18.6 °  = 40.0sin 30.0 ° c ′  = 40.0 sin 18.6 ° sin 30.0 °  = 25.5

This means that the second solution is B ′  = 131.4 °  , C ′  = 18.6 °  ,  and c ′  = 25.5. See Fig. 9.56(c).

EXAMPLE 5 Case 2: Possible solutions

In Example 4, if a > 60.0 ,  only one solution would result. In this case, side a would intercept side c at B. It also intercepts the extension of side c, but this would require that angle A not be included in the triangle (see Fig. 9.57). Thus, only one solution may result if a > b . 

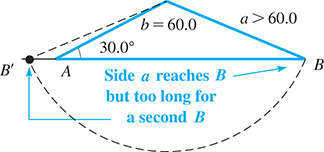
A diagram.

Fig. 9.57

In Example 4, there would be no solution if side a were not at least 30.0. If this were the case, side a would not be long enough to even touch side c. It can be seen that a must at least equal b sin A. If it is just equal to b sin A, there is one solution, a right triangle. See Fig. 9.58.

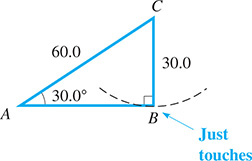
Right triangle Ay B C where angle Ay = 30.0 degrees, angle B = right angle, side ay = 30.0, and side b = 60.0. Side ay just touches vertex B as it swings through.

Fig. 9.58

Summarizing the results for Case 2 as illustrated in Examples 4 and 5, we make the following conclusions. Given sides a and b and angle A [assuming here that a and A (A < 90 ° ) are corresponding parts], we have the following summary of solutions for Case 2.

CAUTION

When two sides and an opposite angle are given, there may be two solutions of the triangle.

NOTE

[Note that in order to have two solutions, we must know two sides and the angle opposite one of the sides, and the shorter side must be opposite the known angle.]

If there is no solution, the calculator will indicate an error. If the solution is a right triangle, the calculator will show an angle of exactly 90 °  (no extra decimal digits will be displayed).

NOTE

[For the reason that two solutions may result for Case 2, it is called the ambiguous case.] However, it must also be kept in mind that there may only be one solution. A careful check of the given parts must be made in order to determine whether there is one solution or two solutions. The following example illustrates Case 2 in an applied problem.

EXAMPLE 6 Case 2—heading of plane

Kingston, Jamaica, is 43.2 °  south of east of Havana, Cuba. What should be the heading of a plane from Havana to Kingston if the wind is from the west at 40.0 km/h and the plane’s speed with respect to the air is 300 km/h?

The heading should be set so that the resultant of the plane’s velocity with respect to the air A and the velocity of the wind W will be in the direction from Havana to Kingston. This means that the resultant velocity R of the plane with respect to the ground must be at an angle of 43.2 °  south of east from Havana.

Using the given information, we draw the vector triangle shown in Fig. 9.60. In the triangle, we know that the angle at Kingston is 43.2 °  by noting the alternate-interior angles (see page 56). By finding θ ,  the required heading can be found. There can be only one solution, because A > W .  Using the law of sines, we have

An equation.
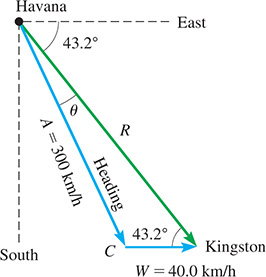
A diagram.

Fig. 9.60

Therefore, the heading should be 43.2 °  + 5.2 °  = 48.4 °  south of east.

If we try to use the law of sines for Case 3 or Case 4, we find that we do not have enough information to complete any of the ratios. These cases can, however, be solved by the law of cosines as shown in the next section.

EXAMPLE 7 Cases 3 and 4 not solvable by law of sines

Given (Case 3) two sides and the included angle of a triangle a = 2 , b = 3 , C = 45 °  ,  and (Case 4) the three sides (Case 4) a = 5 , b = 6 , c = 7 ,  we set up the ratios

(Case 3)2sin A = 3sin B = csin 45 ° and (Case 4)5sin A = 6sin B = 7sin C

The solution cannot be found because each of the three possible equations in either Case 3 or Case 4 contains two unknowns.

EXERCISES 9.5

In Exercises 1 and 2, solve the resulting triangles if the given changes are made in the indicated examples of this section.

  1. In Example 2, solve the triangle if the value of B is changed to 82.94 ° .

  2. In Example 4, solve the triangle if the value of b is changed to 70.0.

In Exercises 3–20, solve the triangles with the given parts.

  1. a = 45.7 , A = 65.0 °  , B = 49.0 ° 

  2. b = 3.07 , A = 26.0 °  , C = 120.0 ° 

  3. c = 4380 , A = 37.4 °  , B = 34.6 ° 

  4. a = 932 , B = 0.9 °  , C = 82.6 ° 

  5. a = 4.601 , b = 3.107 , A = 18.23 ° 

  6. b = 362.2 , c = 294.6 , B = 110.63 ° 

  7. b = 7751 , c = 3642 , B = 20.73 ° 

  8. a = 150.4 , c = 250.9 , C = 76.43 ° 

  9. a = 63.8 , B = 58.4 °  , C = 22.2 ° 

  10. a = 0.130 , A = 55.2 °  , B = 117.5 ° 

  11. b = 4384 , B = 47.43 °  , C = 64.56 ° 

  12. b = 283.2 , B = 13.79 °  , C = 103.62 ° 

  13. a = 5.240 , b = 4.446 , B = 48.13 ° 

  14. a = 89.45 , c = 37.36 , C = 15.62 ° 

  15. b = 2880 , c = 3650 , B = 31.4 ° 

  16. a = 0.841 , b = 0.965 , A = 57.1 ° 

  17. a = 450 , b = 1260 , A = 64.8 ° 

  18. a = 20 , c = 10 , C = 30 ° 

In Exercises 21–38, use the law of sines to solve the given problems.

  1. A small island is approximately a triangle in shape. If the longest side of the island is 520 m, and two of the angles are 45 °  and 55 °  ,  what is the length of the shortest side?

  2. A boat followed a triangular route going from dock A, to dock B, to dock C, and back to dock A. The angles turned were 135 °  at B and 125 °  at C. If B is 875 m from A, how far is it from B to C?

  3. The loading ramp at a delivery service is 12.5 ft long and makes a 18.0 °  angle with the horizontal. If it is replaced with a ramp 22.5 ft long, what angle does the new ramp make with the horizontal?

  4. In an aerial photo of a triangular field, the longest side is 86.0 cm, the shortest side is 52.5 cm, and the largest angle is 82.0 °  .  The scale is 1 cm = 2 m .  Find the actual length of the third side of the field.

  5. The Pentagon (headquarters of the U.S. Department of Defense) is the largest office building in the world. It is a regular pentagon (five sides), 921 ft on a side. Find the greatest straight-line distance from one point on the outside of the building to another outside point (the length of a diagonal).

  6. Two ropes hold a 175-lb crate as shown in Fig. 9.61. Find the tensions T1 and T2 in the ropes. (Hint: Move vectors so that they are tail to head to form a triangle. The vector sum T1 + T2 must equal 175 lb for equilibrium. See page 278.)

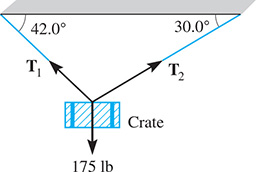
    Vectors T sub 1 and T sub 2 pull up from a crate, meeting the ceiling at angles of 42.0 degrees and 30.0 degrees, respectively. A force of 175 pounds pulls straight down on the crate.

    Fig. 9.61

  7. Find the tension T in the left guy wire attached to the top of the tower shown in Fig. 9.62. (Hint: The horizontal components of the tensions must be equal and opposite for equilibrium. See page 278. Thus, move the tension vectors tail to head to form a triangle with a vertical resultant. This resultant equals the upward force at the top of the tower for equilibrium. This last force is not shown and does not have to be calculated.)

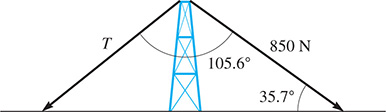
    Vectors T and 850 Newtons pull down from the top of a tower with an angle of 105.6 degrees between them. The vector of 850 Newtons is 35.7 degrees with the ground.

    Fig. 9.62

  8. Find the distance from Atlanta to Raleigh, North Carolina, from Fig. 9.63.

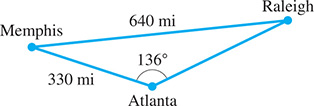
    A triangle between Atlanta, Memphis, and Raleigh. The angle at Atlanta is 136 degrees. From Atlanta to Memphis is 330 miles. From Memphis to Raleigh is 640 miles.

    Fig. 9.63

  9. An Amazon robot begins at point O and travels in a straight line across a warehouse floor to point A where it picks up some merchandise. It then turns a 35 °  corner and travels 32.5 m to point B where it drops off the merchandise. See Fig. 9.64. If the robot must now turn a 29.0 °  corner to return to its original position, how far must it travel to get there?

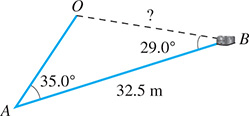
    Triangle O Ay B where angle Ay = 35.0 degrees, side Ay B = 32.5 meters, and angle B = 29.0 degrees. Side O B is unknown.

    Fig. 9.64

  10. When an airplane is landing at an 8250-ft runway, the angles of depression to the ends of the runway are 10.0 °  and 13.5 °  .  How far is the plane from the near end of the runway?

  11. Find the total length of the path of the laser beam that is shown in Fig. 9.65.

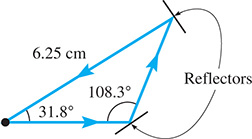
    A laser beam is fired at reflectors, creating a triangle with angle 31.8 degrees, and angle 108.3 degrees with opposite side 6.25 centimeters.

    Fig. 9.65

  12. In widening a highway, it is necessary for a construction crew to cut into the bank along the highway. The present angle of elevation of the straight slope of the bank is 23.0 °  ,  and the new angle is to be 38.5 °  ,  leaving the top of the slope at its present position. If the slope of the present bank is 220 ft long, how far horizontally into the bank at its base must they dig?

  13. A communications satellite is directly above the extension of a line between receiving towers A and B. It is determined from radio signals that the angle of elevation of the satellite from tower A is 89.2 °  ,  and the angle of elevation from tower B is 86.5 °  .  See Fig. 9.66. If A and B are 1290 km apart, how far is the satellite from A? (Neglect the curvature of Earth.)

    A triangle where angle B = 86.5 degrees, exterior angle Ay = 89.2 degrees, and side Ay B is 1,290 kilometers opposite the satellite.

    Fig. 9.66

  14. A Mars rover travels 569 m in a straight line and then stops to take a soil sample. It then changes direction and travels another 642 m where it takes another sample. If it must turn on a 47.2 °  corner to return to its starting point, what are the possible distances from its starting point?

  15. A boat owner wishes to cross a river 2.60 km wide and go directly to a point on the opposite side 1.75 km downstream. The boat goes 8.00 km/h in still water, and the stream flows at 3.50 km/h. What should the boat’s heading be?

  16. A motorist traveling along a level highway at 75 km/h directly toward a mountain notes that the angle of elevation of the mountain top changes from about 20 °  to about 30 °  in a 20-min period. How much closer on a direct line did the mountain top become?

  17. A person standing on level ground from the base of the Skylon Tower in Niagara Falls observes an elevator going up the side of the tower. At one instant, the angle of elevation to the elevator is 42.5 °  and then 15.0 s later, the angle of elevation is 60.7 °  .  If the elevator travels at a rate of 10.0 ft/s, how high above ground is the elevator at the second instant?

  18. Point P on the mechanism shown in Fig. 9.67 is driven back and forth horizontally. If the minimum value of angle θ is 32.0 °  ,  what is the distance between extreme positions of P? What is the maximum possible value of angle θ ? 

    A robotic arm of 36.0 centimeters is at angle theta to the horizontal, and connected by a hinge to a 24.5 centimeter arm that ends with point P. Point P is on the horizontal and able to move back and forth.

    Fig. 9.67

Answers to Practice Exercises

  1. a = 6.34

  2. Two solutions

  3. 46.3 ° 

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.128.79.88