Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

12.6 Products, Quotients, Powers, and Roots of Complex Numbers

Multiplication, Division, and Powers in Polar and Exponential Forms • DeMoivre’s Theorem • Roots

The operations of multiplication and division can be performed with complex numbers in polar and exponential forms, as well as rectangular form. It is convenient to use polar form for multiplication and division as well as for finding powers or roots of complex numbers.

Using exponential form and laws of exponents, we multiply two complex numbers as

[r_{1} e^{j θ_{1}}] \times [r_{2} e^{j θ_{2}}] = r_{1} r_{2} e^{j θ_{1} + j θ_{2}} = r_{1} r_{2} e^{j (θ_{1} + θ_{2})}

$[r_{1} e^{j θ_{1}}] \times [r_{2} e^{j θ_{2}}] = r_{1} r_{2} e^{j θ_{1} + j θ_{2}} = r_{1} r_{2} e^{j (θ_{1} + θ_{2})}$

Rewriting this result in polar form, we have

[r_{1} e^{j θ_{1}}] \times [r_{2} e^{j θ_{2}}] = [r_{1} (\cos θ_{1} + j \sin θ_{1})] \times [r_{2} (\cos θ_{2} + j \sin θ_{2})]

$[r_{1} e^{j θ_{1}}] \times [r_{2} e^{j θ_{2}}] = [r_{1} (\cos θ_{1} + j \sin θ_{1})] \times [r_{2} (\cos θ_{2} + j \sin θ_{2})]$

and

r_{1} r_{2} e^{j (θ_{1} + θ_{2})} = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + j \sin (θ_{1} + θ_{2})]

$r_{1} r_{2} e^{j (θ_{1} + θ_{2})} = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + j \sin (θ_{1} + θ_{2})]$

The polar expressions are equal, which means the product of two complex numbers is

\begin{array}{c} (r_{1} ∠ \underline{θ_{1}}) (r_{2} ∠ \underline{θ_{2}}) = r_{1} r_{2} ∠ \underline{θ_{1} + θ_{2}}, or \\ r_{1} (\cos θ_{1} + j \sin θ_{1}) r_{2} (\cos θ_{2} + j \sin θ_{2}) \\ = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + j \sin (θ_{1} + θ_{2})] \end{array}

$\begin{array}{c} (r_{1} ∠ \underline{θ_{1}}) (r_{2} ∠ \underline{θ_{2}}) = r_{1} r_{2} ∠ \underline{θ_{1} + θ_{2}}, or \\ r_{1} (\cos θ_{1} + j \sin θ_{1}) r_{2} (\cos θ_{2} + j \sin θ_{2}) \\ = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + j \sin (θ_{1} + θ_{2})] \end{array}$ (12.13)

NOTE

[The magnitudes are multiplied, and the angles are added.]

EXAMPLE 1 Multiplication in polar form

To multiply the complex numbers $3.61 ∠ \underline{56.3 °}$ $3.61 ∠ \underline{56.3 °}$ and $1.41 ∠ \underline{315.0 °},$ $1.41 ∠ \underline{315.0 °},$ we have

The process of multiplication of the complex numbers, 3.61 angle 56.3 degree and 1.41 angle 315.0 degree.

.6-2 Full Alternative Text

Note that the angle in the final result is between $0 °$ $0 °$ and $360 °$ $360 °$ . This is usually the case, although in some applications, it is expressed as a negative angle.

If we wish to divide one complex number in exponential form by another, we arrive at the following result:

\frac{r_{1} e^{j θ_{1}}}{r_{2} e^{j θ_{2}}} = \frac{r_{1}}{r_{2}} e^{j (θ_{1} - θ_{2})}

$\frac{r_{1} e^{j θ_{1}}}{r_{2} e^{j θ_{2}}} = \frac{r_{1}}{r_{2}} e^{j (θ_{1} - θ_{2})}$ (12.14)

Therefore, the result of dividing one complex number in polar form by another is given by

\begin{array}{rcl} \frac{r_{1} ∠ \underline{θ_{1}}}{r_{2} ∠ \underline{θ_{2}}} & = & \frac{r_{1}}{r_{2}} ∠ \underline{θ_{1} - θ_{2}}, or \\ \frac{r_{1} (\cos θ_{1} + j \sin θ_{1})}{r_{2} (\cos θ_{2} + j \sin θ_{2})} & = & \frac{r_{1}}{r_{2}} [\cos (θ_{1} - θ_{2}) + j \sin (θ_{1} - θ_{2})] \end{array}

$\begin{array}{rcl} \frac{r_{1} ∠ \underline{θ_{1}}}{r_{2} ∠ \underline{θ_{2}}} & = & \frac{r_{1}}{r_{2}} ∠ \underline{θ_{1} - θ_{2}}, or \\ \frac{r_{1} (\cos θ_{1} + j \sin θ_{1})}{r_{2} (\cos θ_{2} + j \sin θ_{2})} & = & \frac{r_{1}}{r_{2}} [\cos (θ_{1} - θ_{2}) + j \sin (θ_{1} - θ_{2})] \end{array}$ (12.15)

NOTE

[The magnitudes are divided, and the angles are subtracted.]

EXAMPLE 2 Division in polar form

Divide the first complex number of Example 1 by the second.

Using the $r (\cos θ + j \sin θ)$ $r (\cos θ + j \sin θ)$ notation, we have

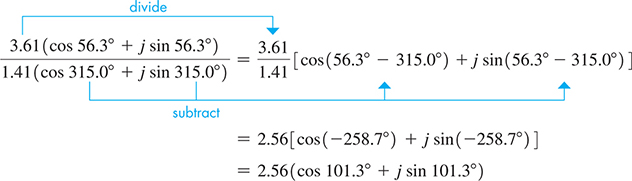
The process of dividing two complex numbers, 3.61 left parenthesis cosine 56.3 degree + j sine 56.3 degree right parenthesis and 1.41 left parenthesis cosine 315.0 degree + j sine 315.0 degree right parenthesis.

.6-2 Full Alternative Text

We have just seen that multiplying and dividing numbers in polar form can be easily performed.

CAUTION

However, if we are to add or subtract numbers given in polar form, we must convert them to rectangular form before we do the addition or subtraction.

EXAMPLE 3 Addition in polar form

Perform the addition $1.563 ∠ \underline{37.56 °} + 3.827 ∠ \underline{146.23 °} .$ $1.563 ∠ \underline{37.56 °} + 3.827 ∠ \underline{146.23 °} .$

In order to do this addition, we must change each number to rectangular form:

\begin{array}{l} 1.563 ∠ \underline{37.56 °} + 3.827 ∠ \underline{146.23 °} \\ = 1.563 (\cos 37.56 ° + j \sin 37.56 °) + 3.827 (\cos 146.23 ° + j \sin 146.23 °) \\ = 1.2390 + 0.9528 j - 3.1813 + 2.1273 j \\ = - 1.9423 + 3.0801 j \end{array}

$\begin{array}{l} 1.563 ∠ \underline{37.56 °} + 3.827 ∠ \underline{146.23 °} \\ = 1.563 (\cos 37.56 ° + j \sin 37.56 °) + 3.827 (\cos 146.23 ° + j \sin 146.23 °) \\ = 1.2390 + 0.9528 j - 3.1813 + 2.1273 j \\ = - 1.9423 + 3.0801 j \end{array}$

Converting back to polar form, we get $3.641 ∠ \underline{122.24 °}$ $3.641 ∠ \underline{122.24 °}$ (see Fig. 12.17).

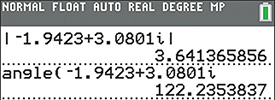
A calculator screen with input absolute value of negative 1.9423 plus 3.0801 i, and output 3.641365856; input angle of, negative 1.9423 plus 3.0801 i, and output 122.2353837. — Fig. 12.17

DEMOIVRE'S THEOREM

To raise a complex number to a power, we use the exponential form of the number along with the properties of exponents ${(a b)}^{n} = a^{n} b^{n}$ ${(a b)}^{n} = a^{n} b^{n}$ and ${(a^{m})}^{n} = a^{m n} .$ ${(a^{m})}^{n} = a^{m n} .$ This leads to

{(r e^{j θ})}^{n} = r^{n} e^{j n θ}

${(r e^{j θ})}^{n} = r^{n} e^{j n θ}$ (12.16)

Extending this to polar form, we have

\begin{array}{rcl} {(r ∠ \underline{θ})}^{n} & = & r^{n} ∠ \underline{n θ}, or \\ {[r (\cos θ + j \sin θ)]}^{n} & = & r^{n} (\cos n θ + j \sin n θ) \end{array}

$\begin{array}{rcl} {(r ∠ \underline{θ})}^{n} & = & r^{n} ∠ \underline{n θ}, or \\ {[r (\cos θ + j \sin θ)]}^{n} & = & r^{n} (\cos n θ + j \sin n θ) \end{array}$ (12.17)

Equation (12.17) is known as DeMoivre’s theorem and is valid for all real values of n. It is also used for finding roots of complex numbers if n is a fractional exponent. We note that the magnitude is raised to the power, and the angle is multiplied by the power.

EXAMPLE 4 Power by DeMoivre‘s theorem

Using DeMoivre’s theorem, find ${(2 + 3 j)}^{3} .$ ${(2 + 3 j)}^{3} .$

Converting to polar form, $2 + 3 j = 3.61 ∠ \underline{56.3 °} .$ $2 + 3 j = 3.61 ∠ \underline{56.3 °} .$ Therefore,

The process of solving the expression, left bracket 3.61 left parenthesis cosine 56.3 degree + j sine 56.3 degree right parenthesis right bracket cubed.

.6-2 Full Alternative Text

Expressing $θ$ $θ$ in radians, we have $θ = 56.3 ° = 0.983 rad .$ $θ = 56.3 ° = 0.983 rad .$ Therefore,

The process of solving the expression, left parenthesis 3.61 e raised to the power of, 0.983 j right parenthesis cubed.

.6-2 Full Alternative Text

EXAMPLE 5 Cube roots by DeMoivre‘s theorem

Find the cube root of $- 1.$ $- 1.$

Because $- 1$ $- 1$ is a real number, we can find its cube root by means of the definition. Since ${(- 1)}^{3} = - 1, \sqrt[3]{- 1} = - 1 .$ ${(- 1)}^{3} = - 1, \sqrt[3]{- 1} = - 1 .$ We check this by DeMoivre’s theorem. Writing $- 1$ $- 1$ in polar form, we have

- 1 = 1 (\cos 180 ° + j \sin 180 °)

$- 1 = 1 (\cos 180 ° + j \sin 180 °)$

Applying DeMoivre’s theorem, with $n = \frac{1}{3},$ $n = \frac{1}{3},$ we obtain

The process of solving the expression, left parenthesis negative 1 right parenthesis to the 1 third power.

.6-2 Full Alternative Text

Observe that we did not obtain $- 1$ $- 1$ as the answer. If we check the answer, in the form $\frac{1}{2} + j \frac{\sqrt{3}}{2},$ $\frac{1}{2} + j \frac{\sqrt{3}}{2},$ by actually cubing it, we obtain $- 1!$ $- 1!$ Therefore, it is a correct answer.

We should note that it is possible to take $\frac{1}{3}$ $\frac{1}{3}$ of any angle up to $1080 °$ $1080 °$ and still have an angle less than $360 °$ $360 °$ . Because $180 °$ $180 °$ and $540 °$ $540 °$ have the same terminal side, let us try writing $- 1$ $- 1$ as $1 (\cos 540 ° + j \sin 540 °) .$ $1 (\cos 540 ° + j \sin 540 °) .$ Using DeMoivre’s theorem, we have

.6-2 Full Alternative Text

We have found the answer we originally anticipated.

Angles of $180 °$ $180 °$ and $900 °$ $900 °$ also have the same terminal side, so we try

.6-2 Full Alternative Text

Checking this, we find that it is also a correct root. We may try $1260 °$ $1260 °$ , but $\frac{1}{3} (1260 °) = 420 °,$ $\frac{1}{3} (1260 °) = 420 °,$ which has the same functional values as $60 °$ $60 °$ , and would give us the answer $0.5000 + 0.8660 j$ $0.5000 + 0.8660 j$ again.

We have found, therefore, three cube roots of $- 1.$ $- 1.$ They are

- 1, \frac{1}{2} + j \frac{\sqrt{3}}{2}, \frac{1}{2} - j \frac{\sqrt{3}}{2}

$- 1, \frac{1}{2} + j \frac{\sqrt{3}}{2}, \frac{1}{2} - j \frac{\sqrt{3}}{2}$

These roots are graphed in Fig. 12.18. Note that they are equally spaced on the circumference of a circle of radius 1.

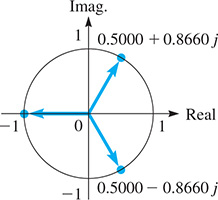
A circle and position vectors. — Fig. 12.18

Figure 12.18 Full Alternative Text

NOTE

[When the results of Example 5 are generalized, it can be proven that there are n nth roots of a complex number.]

When graphed, these roots are on a circle of radius $r^{1 / n}$ $r^{1 / n}$ and are equally spaced $360 ° / n$ $360 ° / n$ apart. Following is the method for finding these n roots.

EXAMPLE 6 Square roots by DeMoivre’s theorem

Find the two square roots of 2j.

First, we write 2j in polar form as $2 j = 2 (\cos 90 ° + j \sin 90 °) .$ $2 j = 2 (\cos 90 ° + j \sin 90 °) .$ To find square roots, we use the exponent 1/2. The first square root is

The process of solving the expression, left parenthesis 2 j right parenthesis to the 1 half power.

.6-2 Full Alternative Text

To find the other square root, we add $360 °$ $360 °$ to $90 °$ $90 °$ . This gives us

{(2 j)}^{1/2} = 2^{1/2} (\cos \frac{450 °}{2} + j \sin \frac{450 °}{2}) = \sqrt{2} (\cos 225 ° + j \sin 225 °) = - 1 - j

${(2 j)}^{1/2} = 2^{1/2} (\cos \frac{450 °}{2} + j \sin \frac{450 °}{2}) = \sqrt{2} (\cos 225 ° + j \sin 225 °) = - 1 - j$

Therefore, the two square roots of 2j are $1 + j$ $1 + j$ and $- 1 - j .$ $- 1 - j .$ We see in Fig. 12.19 that they are on a circle of radius $\sqrt{2}$ $\sqrt{2}$ and $180 °$ $180 °$ apart.

A circle with position vectors that point to 1 plus j in quadrant 1 and negative 1 minus j in quadrant 3. The vectors have opposite directions. — Fig. 12.19

EXAMPLE 7 Sixth roots by DeMoivre’s theorem

Find all the roots of the equation $x^{6} - 64 = 0.$ $x^{6} - 64 = 0.$

Solving for x, we have $x^{6} = 64,$ $x^{6} = 64,$ or $x = \sqrt[6]{64} .$ $x = \sqrt[6]{64} .$ Therefore, we have to find the six sixth roots of 64. Writing 64 in polar form, we have $64 = 64 (\cos 0 ° + j \sin 0 °) .$ $64 = 64 (\cos 0 ° + j \sin 0 °) .$ Using the exponent 1/6 for the sixth root, we have the following solutions:

Six roots of the equation, x to the sixth power minus 64 = 0 are illustrated.

.6-2 Full Alternative Text

These roots are graphed in Fig. 12.20. Note that they are equally spaced $60 °$ $60 °$ apart on the circumference of a circle of radius 2.

Figure 12.20 Full Alternative Text

From the text and examples of this and previous sections, we are able see the uses and advantages of the different forms of complex numbers. These can be summarized as follows:

Rectangular form: Used for all operations; best for addition and subtraction.

Polar form: Used for multiplication, division, powers, roots.

Exponential form: Used for multiplication, division, powers, and theoretical purposes (e.g., deriving DeMoivre’s theorem)

Exercises 12.6

In Exercises 1–4, perform the indicated operations for the resulting complex numbers if the given changes are made in the indicated examples of this section.

In Example 1, change the sign of the angle in the first complex number and then perform the multiplication.
In Example 2, change the sign of the angle in the second complex number and then divide.
In Example 4, change the exponent to 5 and then find the result.
In Example 6, replace 2j with $- 2 j$ $- 2 j$ and then find the roots.

In Exercises 5–20, perform the indicated operations. Leave the result in polar form.

$[4 (\cos 60 ° + j \sin 60 °)] [2 (\cos 20 ° + j \sin 20 °)]$ $[4 (\cos 60 ° + j \sin 60 °)] [2 (\cos 20 ° + j \sin 20 °)]$
$[3 (\cos 120 ° + j \sin 120 °)] [5 (\cos 45 ° + j \sin 45 °)]$ $[3 (\cos 120 ° + j \sin 120 °)] [5 (\cos 45 ° + j \sin 45 °)]$
$(0.5 ∠ \underline{140 °}) (6 ∠ \underline{110 °})$ $(0.5 ∠ \underline{140 °}) (6 ∠ \underline{110 °})$
$(0.4 ∠ \underline{320 °}) (5.5 ∠ \underline{- 150 °})$ $(0.4 ∠ \underline{320 °}) (5.5 ∠ \underline{- 150 °})$
$\frac{8 (\cos 100 ° + j \sin 100 °)}{4 (\cos 65 ° + j \sin 65 °)}$ $\frac{8 (\cos 100 ° + j \sin 100 °)}{4 (\cos 65 ° + j \sin 65 °)}$
$\frac{{[3 (\cos 115 ° + j \sin 115 °)]}^{2}}{45 (\cos 80 ° + j \sin 80 °)}$ $\frac{{[3 (\cos 115 ° + j \sin 115 °)]}^{2}}{45 (\cos 80 ° + j \sin 80 °)}$
$\frac{12 ∠ \underline{320 °}}{5 ∠ \underline{- 210 °}}$ $\frac{12 ∠ \underline{320 °}}{5 ∠ \underline{- 210 °}}$
$\frac{2 ∠ \underline{90 °}}{4 ∠ \underline{75 °}}$ $\frac{2 ∠ \underline{90 °}}{4 ∠ \underline{75 °}}$
${[0.2 (\cos 35 ° + j \sin 35 °)]}^{3}$ ${[0.2 (\cos 35 ° + j \sin 35 °)]}^{3}$
${[3 (\cos 120 ° + j \sin 120 °)]}^{4}$ ${[3 (\cos 120 ° + j \sin 120 °)]}^{4}$
${(2/135 °)}^{8}$ ${(2/135 °)}^{8}$
${(1/142 °)}^{10}$ ${(1/142 °)}^{10}$
$\frac{(50 ∠ \underline{236 °}) (2 ∠ \underline{84 °})}{125 ∠ \underline{47 °}}$ $\frac{(50 ∠ \underline{236 °}) (2 ∠ \underline{84 °})}{125 ∠ \underline{47 °}}$
$\frac{{(6 ∠ \underline{137 °})}^{2}}{(2 ∠ \underline{141 °}) (6 ∠ \underline{195 °})}$ $\frac{{(6 ∠ \underline{137 °})}^{2}}{(2 ∠ \underline{141 °}) (6 ∠ \underline{195 °})}$
$\frac{(4 ∠ \underline{24 °}) (10 ∠ \underline{326 °})}{{(1 ∠ \underline{62 °})}^{3} (8 ∠ \underline{77 °})}$ $\frac{(4 ∠ \underline{24 °}) (10 ∠ \underline{326 °})}{{(1 ∠ \underline{62 °})}^{3} (8 ∠ \underline{77 °})}$
$\frac{(25 ∠ \underline{194 °}) (6 ∠ \underline{239 °})}{(30 ∠ \underline{17 °}) (10 ∠ \underline{29 °})}$ $\frac{(25 ∠ \underline{194 °}) (6 ∠ \underline{239 °})}{(30 ∠ \underline{17 °}) (10 ∠ \underline{29 °})}$

In Exercises 21–24, perform the indicated operations. Express results in polar form. See Example 3.

$2.78 ∠ \underline{56.8 °} + 1.37 ∠ \underline{207.3 °}$ $2.78 ∠ \underline{56.8 °} + 1.37 ∠ \underline{207.3 °}$
$15.9 ∠ \underline{142.6 °} - 18.5 ∠ \underline{71.4 °}$ $15.9 ∠ \underline{142.6 °} - 18.5 ∠ \underline{71.4 °}$
$7085 ∠ \underline{115.62 °} - 4667 ∠ \underline{296.34 °}$ $7085 ∠ \underline{115.62 °} - 4667 ∠ \underline{296.34 °}$
$307.5 ∠ \underline{326.54 °} + 726.3 ∠ \underline{96.41 °}$ $307.5 ∠ \underline{326.54 °} + 726.3 ∠ \underline{96.41 °}$

In Exercises 25–34, change each number to polar form and then perform the indicated operations. Express the result in rectangular and polar forms. Check by performing the same operation in rectangular form.

$(3 + 4 j) (5 - 12 j)$ $(3 + 4 j) (5 - 12 j)$
$(5 j - 2) (- 1 - j)$ $(5 j - 2) (- 1 - j)$
$(7 - 3 j) (8 + j)$ $(7 - 3 j) (8 + j)$
$(1 + 5 j) (4 + 2 j)$ $(1 + 5 j) (4 + 2 j)$
$\frac{21}{3 - 9 j}$ $\frac{21}{3 - 9 j}$
$\frac{40 j}{2 j + 7}$ $\frac{40 j}{2 j + 7}$
$\frac{30 + 40 j}{5 - 12 j}$ $\frac{30 + 40 j}{5 - 12 j}$
$\frac{5 j - 2}{- 1 - j}$ $\frac{5 j - 2}{- 1 - j}$
${(3 + 4 j)}^{4}$ ${(3 + 4 j)}^{4}$
${(- 1 - j)}^{3}$ ${(- 1 - j)}^{3}$

In Exercises 35–40, use DeMoivre’s theorem to find all the indicated roots. Be sure to find all roots.

The two square roots of $4 (\cos 60 ° + j \sin 60 °)$ $4 (\cos 60 ° + j \sin 60 °)$
The three cube roots of $27 (\cos 120 ° + j \sin 120 °)$ $27 (\cos 120 ° + j \sin 120 °)$
The three cube roots of $3 - 4 j$ $3 - 4 j$
The two square roots of $- 5 + 12 j$ $- 5 + 12 j$
The square roots of $1 + j$ $1 + j$
The cube roots of $\sqrt{3} + j$ $\sqrt{3} + j$

In Exercises 41–46, find all of the roots of the given equations.

$x^{4} - 1 = 0$ $x^{4} - 1 = 0$
$x^{3} - 8 = 0$ $x^{3} - 8 = 0$
$x^{3} + 27 j = 0$ $x^{3} + 27 j = 0$
$x^{4} - j = 0$ $x^{4} - j = 0$
$x^{5} + 32 = 0$ $x^{5} + 32 = 0$
$x^{6} + 8 = 0$ $x^{6} + 8 = 0$

In Exercises 47–56, solve the given problems.

Using the results of Example 5, find the cube roots of $- 125.$ $- 125.$
Using the results of Example 6, find the square roots of 32j.
In Example 5, we showed that one cube root of $- 1$ $- 1$ is $\frac{1}{2} - \frac{1}{2} j \sqrt{3} .$ $\frac{1}{2} - \frac{1}{2} j \sqrt{3} .$ Cube this number in rectangular form and show that the result is $- 1.$ $- 1.$
Explain why the two square roots of a complex number are negatives of each other.
The cube roots of $- 1$ $- 1$ can be found by solving the equation $x^{3} + 1 = 0.$ $x^{3} + 1 = 0.$ Find these roots by factoring $x^{3} + 1$ $x^{3} + 1$ as the sum of cubes and compare with Example 5.
The cube roots of 8 can be found by solving the equation $x^{3} - 8 = 0.$ $x^{3} - 8 = 0.$ Find these roots by factoring $x^{3} - 8$ $x^{3} - 8$ as the difference of cubes and compare with Exercise 42.
The electric power p (in W) supplied to an element in a circuit is the product of the voltage e and the current i (in A). Find the expression for the power supplied if $e = 6.80 ∠ \underline{56.3 °}$ $e = 6.80 ∠ \underline{56.3 °}$ volts and $i = 0.0705 ∠ \underline{- 15.8 °}$ $i = 0.0705 ∠ \underline{- 15.8 °}$ amperes.
The displacement d (in in.) of a weight suspended on a system of two springs is $d = 6.03 ∠ \underline{22.5 °} + 3.26 ∠ \underline{76.0 °}$ $d = 6.03 ∠ \underline{22.5 °} + 3.26 ∠ \underline{76.0 °}$ in. Perform the addition and express the answer in polar form.
The voltage across a certain inductor is $V = (8.66 ∠ \underline{90.0 °}) (50.0 ∠ \underline{135.0 °}) / (10.0 ∠ \underline{60.0 °})$ $V = (8.66 ∠ \underline{90.0 °}) (50.0 ∠ \underline{135.0 °}) / (10.0 ∠ \underline{60.0 °})$ volts. Simplify this expression and find the magnitude of the voltage.
In a microprocessor circuit, the current is $I = 3.75 ∠ \underline{15.0 °} μ A$ $I = 3.75 ∠ \underline{15.0 °} μ A$ and the impedance is $Z = 2500 ∠ \underline{- 35.0 °} ohms .$ $Z = 2500 ∠ \underline{- 35.0 °} ohms .$ Find the voltage E in rectangular form. Use $E = I Z .$ $E = I Z .$

Answers to Practice Exercises

$15 ∠ \underline{115 °}$ $15 ∠ \underline{115 °}$
$0.6 ∠ \underline{345 °}$ $0.6 ∠ \underline{345 °}$
$6561 ∠ \underline{40 °}$ $6561 ∠ \underline{40 °}$
$2 + 2 j, - 2 - 2 j$ $2 + 2 j, - 2 - 2 j$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 12.6 Products, Quotients, Powers, and Roots of&#160;Complex&#160;Numbers Products, Quotients, Powers, and Roots of Complex Numbers

Create new playlist

Sign In

Sign Up

Table of Contents for
12.6 Products, Quotients, Powers, and Roots of Complex Numbers Products, Quotients, Powers, and Roots of Complex Numbers