12.3 Graphical Representation of Complex Numbers

  • Complex Plane • Complex Number as a Point • Adding and Subtracting Complex Numbers Graphically

Graphically, we represent a complex number as a point, designated as a + bj ,  in the rectangular coordinate system. The real part is the x-value of the point, and the imaginary part is the y-value of the point. Used in this way, the coordinate system is called the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis.

EXAMPLE 1 Complex numbers in the complex plane

In Fig. 12.3, A represents the complex number 3 − 2j ,  B represents  − 1 + j ,  and C represents  − 2 − 3j .  These complex numbers are represented by the points (3 ,   − 2) , ( − 1 , 1) ,  and ( − 2 ,   − 3) ,  respectively, of the standard rectangular coordinate system.

A coordinate system.

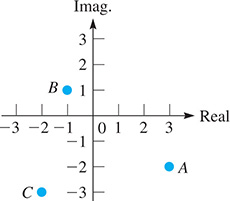
Fig. 12.3

Keep in mind that the meaning given to the points representing complex numbers in the complex plane is different from the meaning given to the points in the standard rectangular coordinate system. A point in the complex plane represents a single complex number, whereas a point in the rectangular coordinate system represents a pair of real numbers.

In the complex plane, consider two complex numbers—for example, 1 + 2j and 3 + j—and their sum 4 + 3j .  Drawing lines from the origin to these points (see Fig. 12.4), note that if we think of the complex numbers as being vectors, their sum is the vector sum. Because complex numbers can be used to represent vectors, the numbers are particularly important. Any complex number can be thought of as representing a vector from the origin to its point in the complex plane. This leads to the method used to add complex numbers graphically.

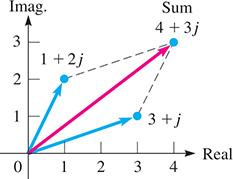
Position vectors. Vector 3 plus j points to (3, 1); vector 1 plus 2 j points to (1, 2), and sum vector 4 plus 3 j points to (4, 3). Dashed segments between vector heads form a parallelogram.

Fig. 12.4

NOTE

[Note that this is equivalent to adding vectors by graphical means.]

EXAMPLE 2 Adding complex numbers graphically

  1. Add the complex numbers 5 − 2j and  − 2 − j graphically.

    The solution is shown in Fig. 12.5. We see that the fourth vertex of the parallelogram is at 3 − 3j .  This is, of course, the algebraic sum of these two complex numbers.

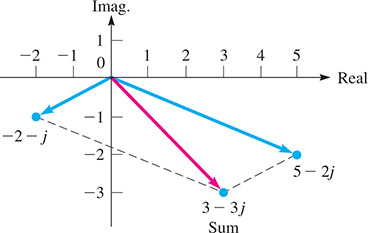
    Position vectors. Vector negative 2 minus j goes to (negative 2, negative 1). Vector 5 minus 2 j goes to (5, negative 2). Sum vector 3 minus 3 j goes to (3, negative 3). Dashed segments between vector heads form a parallelogram.

    Fig. 12.5

  2. Add the complex numbers  − 3 and 1 + 4j . 

    First, note that  − 3 =  − 3 + 0j ,  which means that the point representing  − 3 is on the negative real axis. In Fig. 12.6, we show the numbers  − 3 and 1 + 4j on the graph and complete the parallelogram. From the graph, we see that the sum is  − 2 + 4j . 

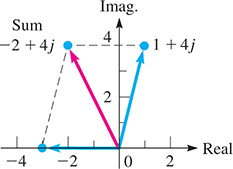
    Position vectors. One goes to (negative 3, 0). Vector 1 plus 4 j goes to (1, 4). Sum vector negative 2 plus 4 j goes to (negative 2, 4). Dashed segments between vector heads form a parallelogram.

    Fig. 12.6

EXAMPLE 3 Subtracting complex numbers graphically

Subtract 4 − 2j from 2 − 3j graphically.

Subtracting 4 − 2j is equivalent to adding  − 4 + 2j .  Therefore, we complete the solution by adding  − 4 + 2j and 2 − 3j ,  as shown in Fig. 12.7. The result is  − 2 − j . 

Position vectors. Vector negative 4 plus 2 j goes to (negative 4, 2). Vector 2 minus 3 j goes to (2, negative 3). Sum vector negative 2 minus j goes to (negative 2, negative 1). Dashed segments between vector heads form a parallelogram.

Fig. 12.7

EXAMPLE 4 Adding complex numbers—forces on a bolt

Two forces acting on an overhead bolt can be represented by 35 − 20j N and  − 50 − 15j N .  Find the resultant force graphically.

The forces are shown in Fig. 12.8. From the graph, we can see that the sum of the forces, which is the resultant force, is  − 15 − 35j N . 

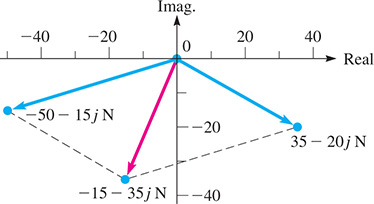
Position vectors.

Fig. 12.8

Exercises 12.3

In Exercises 1 and 2, perform the indicated operations for the resulting complex numbers if the given changes are made in the indicated examples of this section.

  1. In Example 2(a), change the sign of the imaginary part of the second complex number and then add the numbers graphically.

  2. In Example 3, change the sign of the imaginary part of the second complex number and do the subtraction graphically.

In Exercises 3–8, locate the given numbers in the complex plane.

  1. 2 + 6j

  2.  − 5 + j

  3.  − 4 − 3j

  4. 10

  5.  − 3j

  6. 3 − 4j

In Exercises 9–26, perform the indicated operations graphically. Check them algebraically.

  1. 2 + (3 + 4j)

  2. 2j + ( − 2 + 3j)

  3. (5 − j) + (3 + 2j)

  4. (3 − 2j) + ( − 1 − j)

  5. 5j − (1 − 4j)

  6. (0.2 − 0.1j) − 0.1

  7. (2 − 4j) + (j − 2)

  8. ( − 1 − 6j) + (3j + 6)

  9. (3 − 2j) − (4 − 6j)

  10. ( − 25 − 40j) − (20 − 55j)

  11. (80 + 300j) − (260 + 150j)

  12. ( − j − 2) − ( − 1 − 3j)

  13. (3 − j) + (6 + 5j)

  14. (7 + 4j) − (3j − 8)

  15. (3 − 6j) − ( − 1 − 8j)

  16. ( − 6 − 3j) + (2 − 7j)

  17. (2j + 1) − 3j − (j + 1)

  18. (6 − j) − 9 − (2j − 3)

In Exercises 27–30, show the given number, its negative, and its conjugate on the same coordinate system.

  1. 3 + 2j

  2. 4j − 2

  3.  − 3 − 5j

  4. 5 − j

In Exercises 31 and 32, show the numbers a + bj ,  3(a + bj) ,  and  − 3(a + bj) on the same coordinate system. The multiplication of a complex number by a real number is called scalar multiplication of the complex number.

  1. 3 − j

  2.  − 10 − 30j

In Exercises 33–36, perform the indicated vector operations graphically on the complex number 2 + 4j . 

  1. Graph the complex number and its conjugate. Describe the relative positions.

  2. Add the number and its conjugate. Describe the result.

  3. Subtract the conjugate from the number. Describe the result.

  4. Graph the number, the number multiplied by j, the number multiplied by j2 ,  and the number multiplied by j3 on the same graph. Describe the result of multiplying a complex number by j.

In Exercises 37 and 38, perform the indicated vector additions graphically. Check them algebraically.

  1. Two ropes hold a boat at a dock. The tensions in the ropes can be represented by 40 + 10j lb and 50 − 25j lb .  Find the resultant force.

  2. Relative to the air, a plane heads north of west with a velocity that can be represented by  − 480 + 210j km / h .  The wind is blowing from south of west with a velocity that can be represented by 60 + 210j km / h .  Find the resultant velocity of the plane.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.128.199.162