Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

15.3 Rational and Irrational Roots

Rational Root Theorem • Descartes’ Rule of Signs • Roots of a Polynomial Equation

The product $(x + 2) (x - 4) (x + 3)$ $(x + 2) (x - 4) (x + 3)$ equals $x^{3} + x^{2} - 14 x - 24 .$ $x^{3} + x^{2} - 14 x - 24 .$ Here, we find that the constant 24 is determined only by the 2, 4, and 3. These numbers represent the roots of the equation if the given function is set equal to zero. In fact, if we find all the integer roots of an equation with integer coefficients and represent the equation in the form

f (x) = (x - r_{1}) (x - r_{2}) \dots (x - r_{k}) f_{k + 1} (x) = 0

$f (x) = (x - r_{1}) (x - r_{2}) \dots (x - r_{k}) f_{k + 1} (x) = 0$

where all the roots indicated are integers, the constant term of f(x) must have factors of $r_{1}, r_{2}, \dots, r_{k} .$ $r_{1}, r_{2}, \dots, r_{k} .$ This leads us to the theorem that states that

in a polynomial equation $f (x) = 0,$ $f (x) = 0,$ if the coefficient of the highest power is 1, then any integer roots are factors of the constant term of f(x).

EXAMPLE 1 Possible integer roots if `a`₀ = 1

The equation $x^{5} - 4 x^{4} - 7 x^{3} + 14 x^{2} - 44 x + 120 = 0$ $x^{5} - 4 x^{4} - 7 x^{3} + 14 x^{2} - 44 x + 120 = 0$ can be written as

(x - 5) (x + 3) (x - 2) (x^{2} + 4) = 0

$(x - 5) (x + 3) (x - 2) (x^{2} + 4) = 0$

We now note that $5 (3) (2) (4) = 120 .$ $5 (3) (2) (4) = 120 .$ Thus, the roots $5, - 3,$ $5, - 3,$ and 2 are numerical factors of $| 120 |$ $| 120 |$ The theorem states nothing about the signs involved.

If the coefficient $a_{n}$ $a_{n}$ of the highest-power term of f(x) is an integer not equal to 1, the polynomial equation $f (x) = 0$ $f (x) = 0$ may have rational roots that are not integers. We can factor $a_{n}$ $a_{n}$ from every term of f(x). Thus, any polynomial equation $f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0} = 0$ $f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0} = 0$ with integer coefficients can be written in the form

f (x) = a_{n} (x^{n} + \frac{a_{n - 1}}{a_{n}} x^{n - 1} + \dots + \frac{a_{0}}{a_{n}}) = 0

$f (x) = a_{n} (x^{n} + \frac{a_{n - 1}}{a_{n}} x^{n - 1} + \dots + \frac{a_{0}}{a_{n}}) = 0$

Because $a_{0}$ $a_{0}$ and $a_{n}$ $a_{n}$ are integers, $a_{0} / a_{n}$ $a_{0} / a_{n}$ is a rational number. Using the same reasoning as with integer roots applied to the polynomial within the parentheses, we see that any rational roots are factors of $a_{0} / a_{n}$ $a_{0} / a_{n}$ This leads to the following theorem:

EXAMPLE 2 Possible rational roots

If $f (x) = 4 x^{3} - 3 x^{2} - 25 x - 6,$ $f (x) = 4 x^{3} - 3 x^{2} - 25 x - 6,$ any possible rational roots must be integer factors of 6 divided by integer factors of 4. These factors of 6 are 1, 2, 3, and 6, and these factors of 4 are 1, 2, and 4. Forming all possible positive and negative quotients, any possible rational roots that exist will be found in the following list: $\pm 1, \pm \frac{1}{2}, \pm \frac{1}{4}, \pm 2, \pm 3, \pm \frac{3}{2}, \pm \frac{3}{4}, \pm 6 .$ $\pm 1, \pm \frac{1}{2}, \pm \frac{1}{4}, \pm 2, \pm 3, \pm \frac{3}{2}, \pm \frac{3}{4}, \pm 6 .$

The roots of this equation are $- 2, 3,$ $- 2, 3,$ and $- \frac{1}{4} .$ $- \frac{1}{4} .$

There are 16 different possible rational roots in Example 2, but we cannot tell which of these are the actual roots. Therefore we now present a rule, known as Descartes’ rule of signs, which will help us to find these roots.

We can reason this way: If f(x) has all positive terms, then any positive number substituted in f(x) must give a positive value for f(x). This indicates that the number substituted in the function is not a root. Thus, there must be at least one negative and one positive term in the function for any positive number to be a root. This is not a proof, but it does indicate the type of reasoning used in developing the theorem.

EXAMPLE 3 Using Descartes’ rule of signs

By Descartes’ rule of signs, determine the maximum possible number of positive and negative roots of $3 x^{3} - x^{2} - x + 4 = 0 .$ $3 x^{3} - x^{2} - x + 4 = 0 .$

Here, $f (x) = 3 x^{3} - x^{2} - x + 4 .$ $f (x) = 3 x^{3} - x^{2} - x + 4 .$ Reading the terms from left to right, there are two changes in sign, which we can show as follows:

f of x = 3 x cubed minus x squared minus x + 4. This equation has two sign changes, from positive to negative and negative to positive.

Because there are two changes of sign in f(x), there are no more than two positive roots of $f (x) = 0 .$ $f (x) = 0 .$

To find the maximum possible number of negative roots, we must find the number of sign changes in $f (- x) .$ $f (- x) .$ Thus,

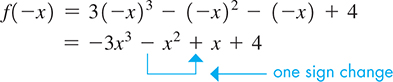
The process depicts the use of Descartes’ rule of signs.

.3-3 Full Alternative Text

NOTE

[When there is just one change of sign in f(x), there is a positive root, and when there is just one change of sign in $f (- x),$ $f (- x),$ there is a negative root.]

There is only one change of sign in $f (- x);$ $f (- x);$ therefore, there is one negative root.

EXAMPLE 4 Using Descartes’ rule of signs

For the equation $4 x^{5} - x^{4} - 4 x^{3} + x^{2} - 5 x - 6 = 0,$ $4 x^{5} - x^{4} - 4 x^{3} + x^{2} - 5 x - 6 = 0,$ we write

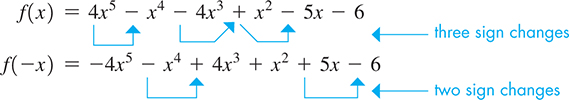
The process depicts the use of Descartes’ rule of signs for f of x and f of negative x.

.3-3 Full Alternative Text

Thus, there are no more than three positive and two negative roots.

At this point, let us summarize the information we can determine about the roots of a polynomial equation $f (x) = 0$ $f (x) = 0$ of degree n and with real coefficients.

Because synthetic division is easy to perform, it is usually used to try possible roots. When a root is found, the quotient is of one degree less than the degree of the dividend. Each root found makes the ensuing work easier. The following examples show the complete method, as well as two other helpful rules.

EXAMPLE 5 Finding roots of equation

Find the roots of the equation $2 x^{3} + x^{2} + 5 x - 3 = 0 .$ $2 x^{3} + x^{2} + 5 x - 3 = 0 .$

Because $n = 3,$ $n = 3,$ there are three roots. If we can find one of these roots, we can use the quadratic formula to find the other two. We have

.3-3 Full Alternative Text

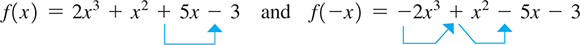
which shows there is one positive root and no more than two negative roots, which may or may not be rational. The possible rational roots are $\pm 1, \pm \frac{1}{2}, \pm \frac{3}{2}, \pm 3 .$ $\pm 1, \pm \frac{1}{2}, \pm \frac{3}{2}, \pm 3 .$

First, trying the root 1 (always a possibility if there are positive roots), we have the synthetic division shown at the left. The remainder of 5 tells us that 1 is not a root, but we have gained some additional information, if we observe closely. If we try any positive number larger than 1, the results in the last row will be larger positive numbers than we now have. The products will be larger, and therefore the sums will also be larger. Thus, there is no positive root larger than 1. This leads to the following rule: This rule tells us that there is no reason to try $+ \frac{3}{2}$ $+ \frac{3}{2}$ and $+ 3$ $+ 3$ as roots. (It is also true that when trying a negative root, if the signs alternate in the bottom row, then there are no roots less than the value tried.)

NOTE

[When we are trying a positive root, if the bottom row contains all positive numbers, then there are no roots larger than the value tried.]

Now, let us try $+ \frac{1}{2},$ $+ \frac{1}{2},$ as shown at the left. The zero remainder tells us that $+ \frac{1}{2}$ $+ \frac{1}{2}$ is a root, and the remaining factor is $2 x^{2} + 2 x + 6,$ $2 x^{2} + 2 x + 6,$ which itself factors to $2 (x^{2} + x + 3) .$ $2 (x^{2} + x + 3) .$ By the quadratic formula, we find the remaining roots by solving the equation $x^{2} + x + 3 = 0 .$ $x^{2} + x + 3 = 0 .$ This gives us

x = \frac{- 1 \pm \sqrt{1 - 12}}{2} = \frac{- 1 \pm j \sqrt{11}}{2}

$x = \frac{- 1 \pm \sqrt{1 - 12}}{2} = \frac{- 1 \pm j \sqrt{11}}{2}$

The three roots are $+ \frac{1}{2}, \frac{- 1 + j \sqrt{11}}{2},$ $+ \frac{1}{2}, \frac{- 1 + j \sqrt{11}}{2},$ and $\frac{- 1 - j \sqrt{11}}{2} .$ $\frac{- 1 - j \sqrt{11}}{2} .$ There are no negative roots because the nonpositive roots are complex. Proceeding this way, we did not have to try any negative roots. The calculator display in Fig. 15.8 verifies the one real root at $x = 1/2 .$ $x = 1/2 .$

The graph y sub 1 = 2 x cubed plus x squared plus 5 x minus 3 rises through (0, negative 3) with decreasing steepness, then inflects at the zero (0.5, 0). — Fig. 15.8

EXAMPLE 6 Finding roots—Bezier curve design

Bezier curves are used frequently in computer graphics to generate smooth curves and surfaces. In particular, cubic Bezier curves are formed by four points, two that define the curve’s start and end (at $t = 0$ $t = 0$ and $t = 1$ $t = 1$ ) and two that “stretch” the middle part of the graph. The red curve in Fig. 15.9 shows a Bezier curve design for the roofline of a new art museum. It is defined by the parametric equations shown below, where the units for x and y are in tens of feet.

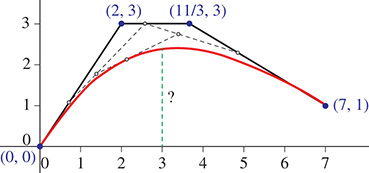
A smooth curve begins at (0, 0), rises to a point above x = 3, then falls to (7, 1). Another graph has line segments from (0, 0) to (2, 3), then to (eleven-thirds, 3), and then to (7, 1). — Fig. 15.9

\begin{array}{l} x & = & 2 t^{3} - t^{2} + 6 t \\ y & = & t^{3} - 9 t^{2} + 9 t \\ 0 \leq t \leq 1 \end{array}

$\begin{array}{l} x & = & 2 t^{3} - t^{2} + 6 t \\ y & = & t^{3} - 9 t^{2} + 9 t \\ 0 \leq t \leq 1 \end{array}$

Find the height of the roofline at the point that is 30 ft to the right of the left edge.

To find this height, we will substitute 3 for x in the top parametric equation, solve for t, and then substitute the result into the bottom equation to find y.

\begin{array}{c} 3 = 2 t^{3} - t^{2} + 6 t \\ 2 t^{3} - t^{2} + 6 t - 3 = 0 \end{array}

$\begin{array}{c} 3 = 2 t^{3} - t^{2} + 6 t \\ 2 t^{3} - t^{2} + 6 t - 3 = 0 \end{array}$

If the above equation has any rational roots, they must be of the form $\frac{\pm 1, \pm 3}{\pm 1, \pm 2} .$ $\frac{\pm 1, \pm 3}{\pm 1, \pm 2} .$ Since we know $0 \leq t \leq 1,$ $0 \leq t \leq 1,$ the only possibilities are $t = \frac{1}{2}$ $t = \frac{1}{2}$ or $t = 1 .$ $t = 1 .$ We also know that $t = 1$ $t = 1$ represents an endpoint, so it is not the solution we desire. Thus, we will try $t = \frac{1}{2}$ $t = \frac{1}{2}$ (or 0.5) using synthetic division.

\begin{array}{r} \begin{array}{r} 2 & - 1 & 6 & - 3 \\ 1 & 0 & 3 \\ 2 & 0 & 6 & 0 \end{array} & \begin{array}{l} 0.5 \end{array} \end{array}

$\begin{array}{r} \begin{array}{r} 2 & - 1 & 6 & - 3 \\ 1 & 0 & 3 \\ 2 & 0 & 6 & 0 \end{array} & \begin{array}{l} 0.5 \end{array} \end{array}$

Since the remainder is zero, $t = 0.5$ $t = 0.5$ is a root (the quotient $2 x^{2} + 6$ $2 x^{2} + 6$ indicates that the other roots are not real numbers). To find the value of y, we substitute $t = 0.5$ $t = 0.5$ into the second parametric equation:

y = {(0.5)}^{3} - 9 {(0.5)}^{2} + 9 (0.5) = 2.375

$y = {(0.5)}^{3} - 9 {(0.5)}^{2} + 9 (0.5) = 2.375$

Therefore, $y = 2.375$ $y = 2.375$ (in tens of ft.), which means the height of the roofline is 23.75 ft at the desired location.

By the methods we have presented, we can look for all roots of a polynomial equation. These include any possible complex roots and exact values of the rational and irrational roots, if they exist. These methods allow us to solve a great many polynomial equations for these roots, but there are numerous other equations for which these methods are not sufficient.

When a polynomial equation has more than two irrational roots, we cannot generally find these roots by the methods we have developed. However, approximate values can be found on a calculator in situations where exact solutions are not needed.

EXAMPLE 7 Finding roots with calculator—box design

The bottom part of a box to hold a jigsaw puzzle is to be made from a rectangular piece of cardboard 37.0 cm by 31.0 cm by cutting out equal squares from the corners, bending up the sides, and taping the corners. See Fig. 15.10. If the volume of the box is to be ${2770 cm}^{3},$ ${2770 cm}^{3},$ find the side of the square that is to be cut out.

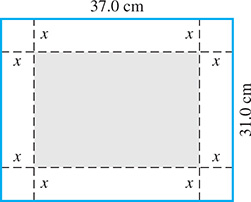
A box with length 37.0 centimeters and width 31.0 centimeters has square corners removed with sides of x each. — Fig. 15.10

Let $x = the$ $x = the$ side of the square to be cut out. This means

\begin{array}{l} 2770 = x (37.0 - 2 x) (31.0 - 2 x) & volume = 2770 {cm}^{3} \\ = 4 x^{3} - 136 x^{2} + 1147 x \\ 4 x^{3} - 136 x^{2} + 1147 x - 2770 = 0 & simplify with terms on the left \end{array}

$\begin{array}{l} 2770 = x (37.0 - 2 x) (31.0 - 2 x) & volume = 2770 {cm}^{3} \\ = 4 x^{3} - 136 x^{2} + 1147 x \\ 4 x^{3} - 136 x^{2} + 1147 x - 2770 = 0 & simplify with terms on the left \end{array}$

The graph of $y = 4 x^{3} - 136 x^{2} + 1147 x - 2770$ $y = 4 x^{3} - 136 x^{2} + 1147 x - 2770$ is shown in Fig. 15.11. Note that there are three positive real roots. This is consistent with there being three changes in sign in the function. However, the domain of the function is $0 < x < 15.5$ $0 < x < 15.5$ since cutting out squares larger than 15.5 cm would leave nothing for the width of the box. Therefore, there are two possible sizes for the squares to be cut from each corner: $x = 4.49 cm$ $x = 4.49 cm$ (this zero is displayed in Fig. 15.11) or $x = 6.79 cm .$ $x = 6.79 cm .$ The third solution, $x = 22.7 cm,$ $x = 22.7 cm,$ is not in the domain.

The graph y sub 1 = 4 x cubed minus 136 x squared plus 1147 x minus 2770 rises through the zero (4.4880227, 0) and into quadrant 1, falls into quadrant 4, then rises. — Fig. 15.11

EXERCISES 15.3

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then perform the indicated operation.

In Example 4, change all signs between terms. (Leave the first term positive.)
In Example 5, change the $+$ $+$ sign before the 5x to $- .$ $- .$

In Exercises 3–20, solve the given equations without using a calculator.

$x^{3} + 5 x^{2} + 2 x - 8 = 0$ $x^{3} + 5 x^{2} + 2 x - 8 = 0$
$2 x^{3} + 5 x^{2} - x + 6 = 0$ $2 x^{3} + 5 x^{2} - x + 6 = 0$
$x^{3} + 2 x^{2} - 5 x - 6 = 0$ $x^{3} + 2 x^{2} - 5 x - 6 = 0$
$t^{3} - 12 t - 16 = 0$ $t^{3} - 12 t - 16 = 0$
$3 x^{4} - x^{2} - 2 x = 0$ $3 x^{4} - x^{2} - 2 x = 0$
$21 t^{3} + 56 t^{2} - 7 = 0$ $21 t^{3} + 56 t^{2} - 7 = 0$
$2 x^{3} - 3 x^{2} - 3 x + 2 = 0$ $2 x^{3} - 3 x^{2} - 3 x + 2 = 0$
$4 x^{3} - 16 x^{2} + 21 x - 9 = 0$ $4 x^{3} - 16 x^{2} + 21 x - 9 = 0$
$x^{4} - 11 x^{2} - 12 x + 4 = 0$ $x^{4} - 11 x^{2} - 12 x + 4 = 0$
$8 x^{4} - 32 x^{3} - x + 4 = 0$ $8 x^{4} - 32 x^{3} - x + 4 = 0$
$5 n^{4} - 2 n^{3} + 40 n - 16 = 0$ $5 n^{4} - 2 n^{3} + 40 n - 16 = 0$
$8 n^{4} - 34 n^{2} + 28 n - 6 = 0$ $8 n^{4} - 34 n^{2} + 28 n - 6 = 0$
$12 x^{4} + 44 x^{3} + 21 x^{2} - 11 x = 6$ $12 x^{4} + 44 x^{3} + 21 x^{2} - 11 x = 6$
$9 x^{4} - 3 x^{3} + 34 x^{2} - 12 x = 8$ $9 x^{4} - 3 x^{3} + 34 x^{2} - 12 x = 8$
$D^{5} + D^{4} - 9 D^{3} - 5 D^{2} + 16 D + 12 = 0$ $D^{5} + D^{4} - 9 D^{3} - 5 D^{2} + 16 D + 12 = 0$
$x^{6} - x^{4} - 14 x^{2} + 24 = 0$ $x^{6} - x^{4} - 14 x^{2} + 24 = 0$
$4 x^{5} - 24 x^{4} + 49 x^{3} - 38 x^{2} + 12 x - 8 = 0$ $4 x^{5} - 24 x^{4} + 49 x^{3} - 38 x^{2} + 12 x - 8 = 0$
$2 x^{5} + 5 x^{4} - 4 x^{3} - 19 x^{2} - 16 x = 4$ $2 x^{5} + 5 x^{4} - 4 x^{3} - 19 x^{2} - 16 x = 4$

In Exercises 21–24, use a calculator to solve the given equations to the nearest 0.01.

$2 x^{3} - 8 x + 3 = 0$ $2 x^{3} - 8 x + 3 = 0$
$2 x^{4} - 15 x^{2} - 7 x + 3 = 0$ $2 x^{4} - 15 x^{2} - 7 x + 3 = 0$
$8 x^{4} + 36 x^{3} + 35 x^{2} - 4 x - 4 = 0$ $8 x^{4} + 36 x^{3} + 35 x^{2} - 4 x - 4 = 0$
$2 x^{5} - 3 x^{4} + 8 x^{3} - 4 x^{2} - 4 x + 2 = 0$ $2 x^{5} - 3 x^{4} + 8 x^{3} - 4 x^{2} - 4 x + 2 = 0$

In Exercises 25–44, solve the given problems. Use a calculator to solve if necessary.

Solve the following system algebraically: $y = x^{4} - 11 x^{2}; y = 12 x - 4$ $y = x^{4} - 11 x^{2}; y = 12 x - 4$
Find rational values of a such that $(x - a)$ $(x - a)$ will divide into $x^{3} + x^{2} - 4 x - 4$ $x^{3} + x^{2} - 4 x - 4$ with a remainder of zero.
Where does the graph of the function $f (x) = 4 x^{3} + 3 x^{2} - 20 x - 15$ $f (x) = 4 x^{3} + 3 x^{2} - 20 x - 15$ cross the x-axis?
Where does the graph of the function $f (s) = 2 s^{4} - s^{3} - 5 s^{2} + 7 s - 6$ $f (s) = 2 s^{4} - s^{3} - 5 s^{2} + 7 s - 6$ cross the s-axis?
By checking only the equation and the coefficients, determine the smallest and largest possible rational roots of the equation $2 x^{4} + x^{2} - 22 x + 8 = 0 .$ $2 x^{4} + x^{2} - 22 x + 8 = 0 .$
By checking only the equation and the coefficients, determine the smallest and largest possible rational roots of the equation $2 x^{4} + x^{2} + 22 x + 26 = 0 .$ $2 x^{4} + x^{2} + 22 x + 26 = 0 .$
The angular acceleration $α$ $α$ (in $rad / s^{2}$ $rad / s^{2}$ ) of the wheel of a car is given by $α = - 0.2 t^{3} + t^{2},$ $α = - 0.2 t^{3} + t^{2},$ where t is the time (in s). For what values of t is $α = 2.0 rad / s^{2} ?$ $α = 2.0 rad / s^{2} ?$
In finding one of the dimensions d (in in.) of the support columns of a building, the equation $3 d^{3} + 5 d^{2} - 400 d - 18,000 = 0$ $3 d^{3} + 5 d^{2} - 400 d - 18,000 = 0$ is found. What is this dimension?
The deflection y of a beam at a horizontal distance x from one end is given by $y = k (x^{4} - 2 L x^{3} - L^{3} x),$ $y = k (x^{4} - 2 L x^{3} - L^{3} x),$ where L is the length of the beam and k is a constant. For what values of x is the deflection zero?
The specific gravity s of a sphere of radius r that sinks to a depth h in water is given by $s = \frac{3 r h^{2} - h^{3}}{4 r^{3}} .$ $s = \frac{3 r h^{2} - h^{3}}{4 r^{3}} .$ Find the depth to which a spherical buoy of radius 4.0 cm sinks if $s = 0.50 .$ $s = 0.50 .$
Cubic Bezier curves are commonly used to control the timing of animations. A certain “ease in” curve is given by $x = 0.1 t^{3} - 1.2 t^{2} + 2.1 t, y = - 2 t^{3} + 3 t^{2}$ $x = 0.1 t^{3} - 1.2 t^{2} + 2.1 t, y = - 2 t^{3} + 3 t^{2}$ for $0 \leq t \leq 1,$ $0 \leq t \leq 1,$ where x represents the percentage of elapsed time for the animation and y represents the percentage of the progression of the animation (both as decimals). What percentage of the animation will be completed after 50% of the time has elapsed? (See chapter introduction.)
The pressure difference p (in kPa) at a distance x (in km) from one end of an oil pipeline is given by $p = x^{5} - 3 x^{4} - x^{2} + 7 x .$ $p = x^{5} - 3 x^{4} - x^{2} + 7 x .$ If the pipeline is 4 km long, where is $p = 0 ?$ $p = 0 ?$
A rectangular tray is made from a square piece of sheet metal 10.0 cm on a side by cutting equal squares from each corner, bending up the sides, and then welding them together. How long is the side of the square that must be cut out if the volume of the tray is ${70.0 cm}^{3} ?$ ${70.0 cm}^{3} ?$
The angle $θ$ $θ$ (in degrees) of a robot arm with the horizontal as a function of time t (in s) is given by $θ = 15 + 20 t^{2} - 4 t^{3}$ $θ = 15 + 20 t^{2} - 4 t^{3}$ for $0 \leq t \leq 5 s .$ $0 \leq t \leq 5 s .$ Find t for $θ = 40 ° .$ $θ = 40 ° .$
The radii of four different-sized ball bearings differ by 1.00 mm in radius from one size to the next. If the volume of the largest equals the volumes of the other three combined, find the radii.
A rectangular safe is to be made of steel of uniform thickness, including the door. The inside dimensions are 1.20 m, 1.20 m, and 2.00 m. If the volume of steel is ${1.25 m}^{3},$ ${1.25 m}^{3},$ find its thickness.
Elliptic curve cryptography uses equations of the form $y^{2} = x^{3} + a x + b$ $y^{2} = x^{3} + a x + b$ and a type of point addition where the “sum” R of points P and Q is found by extending a line through P and Q, determining the third point where the line intersects the curve, and then reflecting that point across the x-axis. For the curve $y^{2} = x^{3} - 6 x + 9,$ $y^{2} = x^{3} - 6 x + 9,$ find the coordinates of point R for $P (- 3, 0)$ $P (- 3, 0)$ and Q (0, 3). See Fig. 15.12.

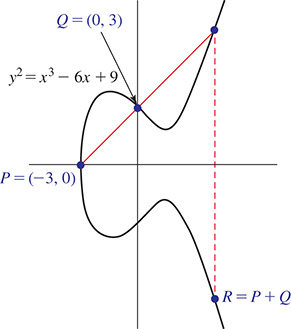
Fig. 15.12

Figure 15.12 Full Alternative Text
Each of three revolving doors has a perimeter of 6.60 m and revolves through a volume of ${9.50 m}^{3}$ ${9.50 m}^{3}$ in one revolution about their common vertical side. What are the door’s dimensions?
If a, b, and c are positive integers, find the combinations of the possible positive, negative, and nonreal complex roots if $f (x) = a x^{3} - b x^{2} + c = 0 .$ $f (x) = a x^{3} - b x^{2} + c = 0 .$
An equation $f (x) = 0$ $f (x) = 0$ involves only odd powers of x with positive coefficients. Explain why this equation has no real root except $x = 0 .$ $x = 0 .$

Answers to Practice Exercises

3 positive, 1 negative
$- 1,$ $- 1,$ 2/3, 2/3, 1

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 15.3 Rational and Irrational Roots

Create new playlist

Sign In

Sign Up

Table of Contents for
15.3 Rational and Irrational Roots