17.3 Solving Nonlinear Inequalities
Critical Values • Solving Polynomial and Rational Inequalities • Solving Inequalities Graphically
In this section, we develop methods of solving inequalities with polynomials, rational expressions (expressions involving fractions), and nonalgebraic expressions. To develop the basic method for solving these types of inequalities, we now take another look at a linear inequality.
In Fig. 17.18, we see that all values of the linear function are positive on one side of the point at which and all values of f(x) are negative on the opposite side of the same point. The means that we can solve a linear inequality by expressing it with zero on the right and then finding the sign of the resulting function on either side of zero.
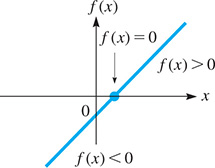
Fig. 17.18
EXAMPLE 1 Sign of function with zero on right
Solve the inequality
Finding the equivalent inequality with zero on the right, we have Setting the left member equal to zero, we have
which means has one sign for and the other sign for Testing values in these intervals, we find, for example, that
Therefore, the solution to the original inequality is The solution in Fig. 17.19(b) corresponds to the positive values of f(x) in Fig. 17.19(a).
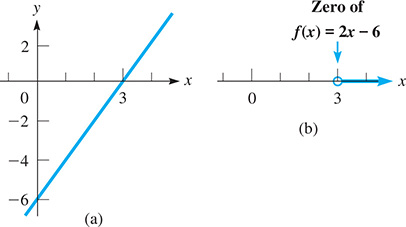
Fig. 17.19
NOTE
[We could have solved this inequality by methods of the previous section, but the important idea here is to use the sign of the function, with zero on the right.]
We can extend this method to solving inequalities with polynomials of higher degree. We first find the equivalent inequality with zero on the right and then find the zeros of the function on the left (often by factoring and setting each factor equal to zero). The function can only change sign at these zeros. Thus, we can solve the inequality by determining the sign of the function on either side of each of the zeros.
This method is especially useful in solving rational inequalities (inequalities involving fractions). A fraction is zero if its numerator equals zero and is undefined if its denominator equals zero. The values of x for which a function is zero or undefined are called the critical values of the function. As all negative and positive values of x are considered (starting with negative numbers of large absolute value, proceeding through zero, and ending with large positive numbers), a function can change sign only at a critical value.
We now outline the method of solving an inequality by using the critical values of the function. Several examples of the method follow.
EXAMPLE 2 Solving a quadratic inequality
Solve the inequality
We first find the equivalent inequality with zero on the right. Therefore, we have We then factor the left member and have
Setting each factor equal to zero, we find the critical values are and 3. These critical values are the only possible places where the function can change in sign. Therefore, we must determine the sign of f(x) for each of the intervals and
To do this, we will choose a test value from each interval and substitute it into the function to determine its sign. The following table shows each interval, the test value, the sign of each factor on each interval, and the resulting sign of the function.
Interval |
Test value |
Sign of |
|
|---|---|---|---|
| 0 | |||
| 4 |
Because we want values for which the product is greater than zero (or positive), the solution is or
The solution that is shown in Fig. 17.20(b) corresponds to the positive values of the function shown in Fig. 17.20(a).

Fig. 17.20
EXAMPLE 3 Solving a cubic inequality
Solve the inequality
By methods developed in Chapter 15, we factor the function on the left and obtain The critical values are We wish to determine the sign of the left member for the intervals and The following table shows this information.
Interval |
Test value |
Sign of f(x) |
|
|---|---|---|---|
| 0 | |||
| 2.5 | |||
| 4 |
Because we want values for the solution is or The solution shown in Fig. 17.21(b) corresponds to the values of in Fig. 17.21(a).

Fig. 17.21
The following example illustrates an applied situation that involves the solution of an inequality.
EXAMPLE 4 Solving a quadratic inequality—force on a cam
The force F (in N) acting on a cam varies according to the time t (in s), and it is given by the function For what values of t, is the force at least 4 N?
For a force of at least 4 N, we know that or This means we are to solve the inequality and the solution is as follows:
The critical values are and which leads to the following table:
Interval |
Test value |
Sign of |
|
|---|---|---|---|
| 1 | |||
| 3 | |||
| 5 |
We see that the values of t that satisfy the greater than part of the problem are and Because we know that for and the solution is
The graph of is shown in Fig. 17.22(a). The solution, shown in Fig. 17.22(b), corresponds to the values of f(t) that are zero or positive or for which
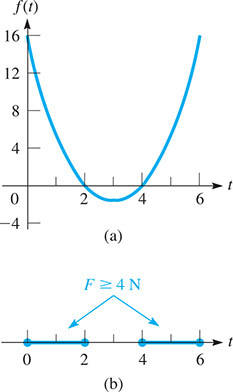
Fig. 17.22
We note here that if the cam rotates in 6-s intervals, the force on the cam is periodic, varying from 2 N to 20 N.
EXAMPLE 5 Solving a rational inequality
Solve the inequality
Since this function is a fraction, the critical values are the values of x that make either the numerator or denominator equal to zero. Thus, the critical values are and 4, and we have the following table:
Interval |
Test value |
Sign of |
|
|---|---|---|---|
| 0 | |||
| 3 | |||
| 5 |
Thus, the solution is or The graph of the function is shown in Fig. 17.23(a), and the graph of the solution is shown in Fig. 17.23(b).
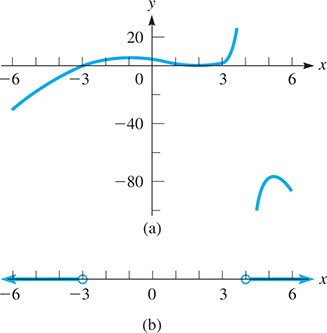
Fig. 17.23
EXAMPLE 6 Solving a rational inequality
Solve the inequality
CAUTION
It seems that all we have to do is multiply both members by and solve the resulting linear inequality. However, this will lead to an incorrect result. The reason is that we assume is positive when we multiply, but is negative for
To avoid this problem, first subtract 2 from each member and combine terms on the left. Therefore, the solution is
NOTE
[This procedure should be used with any inequality involving fractions with the variable in the denominator.]
The critical values are 1 and 5, and we have the following table of signs:
Interval |
Test value |
Sign of |
|
|---|---|---|---|
| 0 | |||
| 3 | |||
| 6 |
Thus, the solution is The graph of is shown in Fig. 17.24(a), and the graph of the solution is shown in Fig. 17.24(b). The solution can also be checked on a calculator using the method shown in the previous section. See Fig. 17.25.

Fig. 17.24

Fig. 17.25
EXAMPLE 7 Values representing real numbers
Find the values of x for which represents a real number.
For the expression to represent a real number, the fraction under the radical must be greater than or equal to zero. This means we must solve the inequality.
The critical values are and 3. After testing each of the three intervals, we find that the function is positive for or Now we must determine if the endpoints and 3 are solutions. The value is a solution because it makes the numerator of the fraction (and therefore the whole fraction) equal to zero. The value is not a solution since it causes division by zero.
Therefore, the solution of the inequality is or and this means these are the values for which the original expression represents a real number. The graph of is shown in Fig. 17.26(a), and the graph of the solution is shown in Fig. 17.26(b).
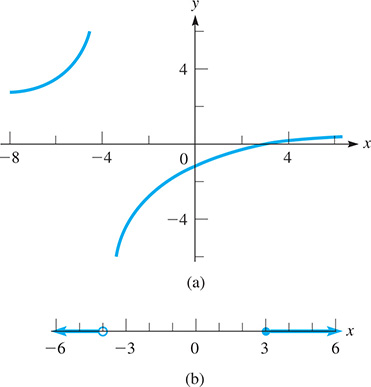
Fig. 17.26
SOLVING INEQUALITIES GRAPHICALLY
We can get an approximate solution of an inequality from the graph of a function, including functions that are not factorable or not algebraic. The method follows several of the earlier examples. First, write the equivalent inequality with zero on the right and then graph this function. Those values of x corresponding to the proper values of y (either above or below the x-axis) are those that satisfy the inequality.
EXAMPLE 8 Solving an inequality graphically
Use a calculator to solve the inequality
Finding the equivalent inequality with zero on the right, we have On the calculator, we then let and graph this function, which is shown in Fig. 17.27.

Fig. 17.27
Using the zero feature, we find that the zero of the function is approximately Because we want values of x that correspond to positive values of y, we see that the solution is
EXERCISES 17.3
In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting inequalities.
In Example 2, change the sign before the 3 to and change 2x to 4x, then solve the resulting inequality, and graph the solution.
In Example 5, change the exponent on from 2 to 3, then solve the resulting inequality, and graph the solution.
In Exercises 3–22, solve the given inequalities. Graph each solution. It is suggested that you also graph the function on a calculator as a check.
In Exercises 23–30, solve the inequalities by displaying the solutions on a calculator. See Examples 9 and 10 in Section 17.2.
In Exercises 31–34, determine the values for x for which the radicals represent real numbers.
In Exercises 35–42, solve the given inequalities graphically by using a calculator. See Example 8. Round all decimals to the nearest hundredth.
In Exercises 43–50, use inequalities to solve the given problems.
 Is for all x? Explain.
Is for all x? Explain. Is for all x? Explain.
Is for all x? Explain.Find an inequality of the form with for which the solution is
Find an inequality of the form with for which the solution is or .
Algebraically find the values of x for which
Graphically find the values of x for which
For what values of real numbers a and b does the inequality have real solutions?
Algebraically find the intervals for which is positive and those for which it is negative. Using only this information, draw a rough sketch of the graph of the function.
In Exercises 51–62, answer the given questions by solving the appropriate inequalities.
The power p (in W) used by a motor is given by where t is the time (in min). For what values of t is the power greater than 15 W?
The weight w (in tons) of fuel in a rocket after launch is where t is the time (in min). During what period of time is the weight of fuel greater than 500 tons?
The weekly sales S (in thousands of units) t weeks after a new smartwatch is released on the market is given by When will the sales be 4000 units or more?
The object distance p (in cm) and image distance q (in cm) for a camera of focal length 3.00 cm is given by For what values of q is
The total capacitance C of capacitors and in series is If find if
A rectangular field is to be enclosed by a fence and divided down the middle by another fence. The middle fence costs $4/ft and the other fence cost $8/ft. If the area of the field is to be and the cost of the fence cannot exceed $4000, what are the possible dimensions of the field?
The weight w (in N) of an object h meters above the surface of Earth is where r is the radius of Earth and is the weight of the object at sea level. Given that if an object weighs 200 N at sea level, for what altitudes is its weight less than 100 N?
The value V after two years of an amount A invested at an annual interest rate r is If $10,000 is invested in order that the value V is between $11,000 and $11,500, what rates of interest (to 0.1%) will provide this?
A triangular postage stamp is being designed such that the height h is 1.0 cm more than the base b. Find the possible height h such that the area of the stamp is at least
A laser source is 2.0 in. from the nearest point P on a flat mirror, and the laser beam is directed at a point Q that is on the mirror and is x in. from P. The beam is then reflected to the receiver, which is x in. from Q. What is x if the total length of the beam is greater than 6.5 in.? See Fig. 17.28.

Fig. 17.28
A plane takes off from Winnipeg and flies due east at 620 km/h. At the same time, a second plane takes off from the surface of Lake Winnipeg 310 km due north of Winnipeg and flies due north at 560 km/h. For how many hours are the planes less than 1000 km apart?
An open box (no top) is formed from a piece of cardboard 8.00 in. square by cutting equal squares from the corners, turning up the resulting sides, and taping the edges together. Find the edges of the squares that are cut out in order that the volume of the box is greater than See Fig. 17.29.

Fig 17.29
Answers to Practice Exercises
or
