4.1 Angles

  • Positive and Negative Angles • Coterminal Angles • Angle Conversions • Standard Position of an Angle

In Chapter 2, we gave a basic definition of an angle. In this section, we extend this definition and also give some other important definitions related to angles.

An angle is generated by rotating a ray about its fixed endpoint from an initial position to a terminal position. The initial position is called the initial side of the angle, the terminal position is called the terminal side, and the fixed endpoint is the vertex. The angle itself is the amount of rotation from the initial side to the terminal side.

If the rotation of the terminal side from the initial side is counterclockwise, the angle is defined as positive. If the rotation is clockwise, the angle is negative. In Fig. 4.1,  ∠ 1 is positive and  ∠ 2 is negative.

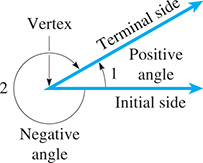
A diagram of an angle.

Fig. 4.1

Many symbols are used to designate angles. Among the most widely used are certain Greek letters such as θ (theta), ϕ (phi), α (alpha), and β (beta). Capital letters representing the vertex (e.g.,  ∠ A or simply A) and other literal symbols, such as x and y, are also used commonly.

In Chapter 2, we introduced two measurements of an angle. These are the degree and the radian. Since degrees and radians are both important, we will briefly review the relationship between them in this section. However, we will not make use of radians until Chapter 8.

From Section 2.1, we recall that a degree is 1/360 of one complete rotation. In Fig. 4.2,  ∠ θ = 30 °  ,  ∠ ϕ = 140 °  ,  ∠ α = 240 °  ,  and  ∠ β =  − 120 °  .  Note that β is drawn in a clockwise direction to show that it is negative. The other angles are drawn in a counterclockwise direction to show that they are positive angles.

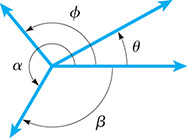
Four angles with an initial side and 3 terminal sides. The three counterclockwise angles at theta, phi, and alpha to the first, second, and third terminal sides, respectively. A clockwise angle of beta goes to the third terminal side.

Fig. 4.2

In Chapter 2, we used degrees and decimal parts of a degree. Most calculators use degrees in this decimal form. Another traditional way is to divide a degree into 60 equal parts called minutes; each minute is divided into 60 equal parts called seconds. The symbols  ′  and  ″  are used to designate minutes and seconds, respectively.

In Fig. 4.2, we note that angles α and β have the same initial and terminal sides. Such angles are called coterminal angles. An understanding of coterminal angles is important in certain concepts of trigonometry.

EXAMPLE 1 Coterminal angles

Determine the measures of two angles that are coterminal with an angle of 145.6 ° .

Because there are 360 °  in one complete rotation, we can find a coterminal angle by adding 360 °  to the given angle of 145.6 °  to get 505.6 ° . Another coterminal angle can be found by subtracting 360 °  from 145.6 °  to get  − 214.4 °  .  See the angles in Fig. 4.3. We could continue to add 360 ° , or subtract 360 ° , as many times as needed to get as many additional coterminal angles as may be required.

Three angles between two rays. The counterclockwise angle is 145.6 degrees. A counterclockwise angle with 1 full rotation that continues to the terminal side is 505.6 degrees. The clockwise angle is negative 214.4 degrees.

Fig. 4.3

ANGLE CONVERSIONS

NOTE

[Therefore, when using a calculator, be sure to use the mode feature to set the calculator for degrees.]

We will use only degrees as a measure of angles in most of this chapter. In later chapters, we will use radians. We can convert between degrees and radians by using a calculator feature or by the definition (see Section 2.4) of π rad = 180 °  . 

Before the extensive use of calculators, it was common to use degrees and minutes in tables, whereas calculators use degrees and decimal parts of a degree. Changing from one form to another can be done directly on a calculator by use of the dms (degree-minute-second) feature. The following examples illustrate angle conversions by using the definitions and by using the appropriate calculator features.

EXAMPLE 2 Convert radians to degrees

Express 1.36 rad in degrees.

We know that π rad = 180 °  ,  which means 1 rad = 180 °  / π .  Therefore,

1.36 rad = 1.36(180 ° π) = 77.9 ° to nearest 0.1° 

This angle is shown in Fig. 4.4. We again note that degrees and radians are simply two different ways of measuring an angle.

A counterclockwise angle of 1.36 radians = 77.9 degrees.

Fig. 4.4

In Fig. 4.5, a calculator display shows the conversions of 1.36 rad to degrees (calculator in degree mode) and 77.9 °  to radians (calculator in radian mode).

A calculator screen with input 1.36 radians, and output 77.92226014; input 77.9 degrees, output 1.359611487.

Fig. 4.5

EXAMPLE 3 Degrees, minutes—decimal form

  1. We change 17 ° 53 ′  to decimal form by using the fact that 1 °  = 60 ′  .  This means that 53 ′  = (5360) °  = 0.88 °  (to nearest 0.01 ° ). Therefore, 17 ° 53 ′  = 17.88 °  .  See Fig. 4.6.

    A counterclockwise angle of 17 degrees 53 minutes = 17.88 degrees.

    Fig. 4.6

  2. The angle between two laser beams is 154.36 ° . To change this to an angle measured to the nearest minute, we have

    0.36 °  = 0.36(60 ′ ) = 22 ′ 

This means that 154.36 °  = 154 ° 22 ′  .  See Fig. 4.7.

A counterclockwise angle of 154.36 degrees = 154 degrees 22 minutes.

Fig. 4.7

STANDARD POSITION OF AN ANGLE

If the initial side of the angle is the positive x-axis and the vertex is the origin, the angle is said to be in standard position. The angle is then classified by the position of the terminal side. If the terminal side is in the first quadrant, the angle is called a first-quadrant angle. Similar terms are used when the terminal side is in the other quadrants. If the terminal side coincides with one of the axes, the angle is a quadrantal angle. For an angle in standard position, the terminal side can be determined if we know any point, except the origin, on the terminal side.

EXAMPLE 4 Angles in standard position

  1. A standard position angle of 60 °  is a first-quadrant angle with its terminal side 60 °  from the x-axis. See Fig. 4.8(a).

    Six graphs are angles in standard position.

    Fig. 4.8

  2. A second-quadrant angle of 130 °  is shown in Fig. 4.8(b).

  3. A third-quadrant angle of 225 °  is shown in Fig. 4.8(c).

  4. A fourth-quadrant angle of 340 °  is shown in Fig. 4.8(d).

  5. A standard-position angle of  − 120 °  is shown in Fig. 4.8(e). Because the terminal side is in the third quadrant, it is a third-quadrant angle.

  6. A standard-position angle of 90 °  is a quadrantal angle since its terminal side is the positive y-axis. See Fig. 4.8(f).

EXAMPLE 5 Standard position—terminal side

In Fig. 4.9, θ is in standard position, and the terminal side is uniquely determined by knowing that it passes through the point (2, 1). The same terminal side passes through the points (4, 2) and (112 ,  114) ,  among an unlimited number of other points. Knowing that the terminal side passes through any one of these points makes it possible to determine the terminal side of the angle.

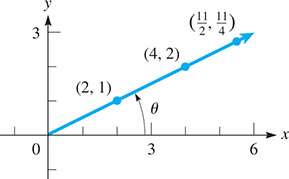
A terminal side with a counterclockwise angle of theta rises through (2, 1), (4, 2), and (11 over 2, 11 over 4).

Fig. 4.9

EXERCISES 4.1

In Exercises 1–4, find the indicated angles in the given examples of this section.

  1. In Example 1, find another angle that is coterminal with the given angle.

  2. In Example 3, change 53 ′  to 35 ′  and then find the decimal form.

  3. In Example 4, find another standard-position angle that has the same terminal side as the angle in Fig. 4.8(c).

  4. In Example 4, find another standard-position angle that has the same terminal side as the angle in Fig. 4.8(e).

In Exercises 5–8, draw the given angles in standard position.

  1. 60 °  , 120 °  ,  − 90 ° 

  2. 330 °  ,  − 150 °  , 450 ° 

  3. 50 °  ,  − 120 °  ,  − 30 ° 

  4. 45 °  , 245 °  ,  − 250 ° 

In Exercises 9–14, determine one positive and one negative coterminal angle for each angle given.

  1. 125 ° 

  2. 173 ° 

  3.  − 150 ° 

  4. 462 ° 

  5. 278.1 ° 

  6.  − 197.6 ° 

In Exercises 15–18, by means of the definition of a radian, change the given angles in radians to equal angles expressed in degrees to the nearest 0.01 ° .

  1. 0.675 rad

  2. 0.838 rad

  3. 4.447 rad

  4.  − 3.642 rad

In Exercises 19–22, use a calculator conversion sequence to change the given angles in radians to equal angles expressed in degrees to the nearest 0.01 ° .

  1. 1.257 rad

  2. 2.089 rad

  3.  − 4.110 rad

  4. 6.705 rad

In Exercises 23–26, use a calculator conversion sequence to change the given angles to equal angles expressed in radians to three significant digits.

  1. 85.0 ° 

  2. 237.4 ° 

  3. 384.8 ° 

  4.  − 117.5 ° 

In Exercises 27–30, change the given angles to equal angles expressed to the nearest minute.

  1. 47.50 ° 

  2. 715.80 ° 

  3.  − 5.62 ° 

  4. 142.87 ° 

In Exercises 31–34, change the given angles to equal angles expressed in decimal form to the nearest 0.01 ° .

  1. 15 ° 12 ′ 

  2. 517 ° 39 ′ 

  3. 301 ° 16 ′ 

  4.  − 94 ° 47 ′ 

In Exercises 35–42, draw angles in standard position such that the terminal side passes through the given point.

  1. (4, 2)

  2. ( − 3 , 8)

  3. ( − 3 ,  − 5)

  4. (6 ,  − 1)

  5. ( − 7 , 5)

  6. ( − 4 ,  − 2)

  7. ( − 2 , 0)

  8. (0, 6)

In Exercises 43–50, the given angles are in standard position. Designate each angle by the quadrant in which the terminal side lies, or as a quadrantal angle.

  1. 31 ° , 310 ° 

  2. 180 ° , 92 ° 

  3. 435 °  ,  − 270 ° 

  4.  − 5 °  , 265 ° 

  5. 1 rad, 2 rad

  6. 3 rad,  − 3π rad

  7. 4 rad, π / 3 rad

  8. 12 rad,  − 2 rad

In Exercises 51 and 52, change the given angles to equal angles expressed in decimal form to the nearest 0.001 ° . In Exercises 53 and 54, change the given angles to equal angles expressed to the nearest second.

  1. 21 ° 42 ′ 36 ″ 

  2.  − 107 ° 16 ′ 23 ″ 

  3. 86.274 ° 

  4. 257.019 ° 

  5. A circular gear rotates clockwise by exactly 3.5 revolutions. By how many degrees does it rotate?

  6. A windmill rotates 15.6 revolutions in a counterclockwise direction. By how many radians does it rotate?

Answers to Practice Exercises

  1. 17.4 ° 

  2. 38 ° 15 ′ 

  3. (e)

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.118.45.162