11.1 Simplifying Expressions with Integer Exponents

  • Laws of Exponents • Simplifying Expressions • Zero and Negative Exponents

The laws of exponents were given in Section 1.4. For reference, they are

am × an = am + n
am × an = am + n
(11.1)
aman = am − nor aman = 1an − m(a ≠ 0)
aman = am − nor aman = 1an − m(a ≠ 0)
(11.2)
(am)n = amn
(am)n = amn
(11.3)
(ab)n = anbn , (ab)n = anbn(b ≠ 0)
(ab)n = anbn , (ab)n = anbn(b ≠ 0)
(11.4)
a0 = 1(a ≠ 0)
a0 = 1(a ≠ 0)
(11.5)
a − n = 1an(a ≠ 0)
a − n = 1an(a ≠ 0)
(11.6)

Although Eqs. (11.1) to (11.4) were originally defined for positive integers as exponents, we showed in Section 1.4 that with the definitions in Eqs. (11.5) and (11.6), they are valid for all integer exponents. Later in the chapter, we will show how fractions are used as exponents. These equations are very important to the developments of this chapter and should be reviewed and learned thoroughly.

EXAMPLE 1 Simplifying basic expressions

  1. Applying Eq. (11.1) and then Eq. (11.6), we have

    a3 × a − 5 = a3 − 5 = a − 2 = 1a2
    a3 × a − 5 = a3 − 5 = a − 2 = 1a2

    Negative exponents are generally not used in the expression of the final result, unless specified otherwise. However, they are often used in intermediate steps.

  2. Applying Eq. (11.1), then (11.6), and then (11.4), we have

    (103 × 10 − 4)2 = (103 − 4)2 = (10 − 1)2 = (110)2 = 1102 = 1100
    (103 × 10 − 4)2 = (103 − 4)2 = (10 − 1)2 = (110)2 = 1102 = 1100

The result is in proper form as either 1 / 102 or 1 / 1001 / 102 or 1 / 100. If the exponent is large, it is common to leave the exponent in the answer.

NOTE

[If the power of ten is being used as part of scientific notation, then the form with the negative exponent 10 − 210 − 2 is used.]

EXAMPLE 2 Simplifying basic expressions

  1. Applying Eqs. (11.2) and (11.5), we have

    a2b3c0ab7 = a2 − 1(1)b7 − 3 = ab4
    a2b3c0ab7 = a2 − 1(1)b7 − 3 = ab4

  2. Applying Eqs. (11.4) and (11.3), and then (11.6), we have

    (x − 2y)3 = (x − 2)3(y3) = x − 6y3 = y3x6
    (x − 2y)3 = (x − 2)3(y3) = x − 6y3 = y3x6

Often, several different combinations of Eqs. (11.1) to (11.6) can be used to simplify an expression. This is illustrated in the next example.

EXAMPLE 3 Simplification done in different ways

  1. (x2y)2(2x) − 2 = (x4y2)(2x)2 = x4y24x2 = x4y21 × x24 = x6y24(x2y)2(2x) − 2 = (x4y2)(2x)2 = x4y24x2 = x4y21 × x24 = x6y24

  2. (x2y)2(2x) − 2 = (x4y2)(2 − 2x − 2) = (x4y2)(x222) = x6y24(x2y)2(2x) − 2 = (x4y2)(2 − 2x − 2) = (x4y2)(x222) = x6y24

    In (a), we first used Eq. (11.6) and then (11.4). The simplification was completed by changing the division of a fraction to multiplication and using Eq. (11.1). In (b), we first used Eq. (11.3), then (11.6), and finally (11.1).

EXAMPLE 4 Exponents and units of measurement

When writing a denominate number, if units of measurement appear in the denominator, they can be written using negative exponents. For example, the metric unit for pressure is the pascal, where 1 Pa  =  1 N/m21 Pa  =  1 N/m2. This can be written as

1 Pa  =  1 N/m2  =  1 N  ⋅  m–2
1 Pa  =  1 N/m2  =  1 N  ⋅  m–2

where 1 / m2 = m − 2 . 1 / m2 = m − 2 . 

The metric unit for energy is the joule, where 1 J  =  1 kg  ⋅  (m  ⋅  s–1)2 , 1 J  =  1 kg  ⋅  (m  ⋅  s–1)2 ,  or

1 J = 1 kg ⋅ m2 ⋅ s − 2 = 1 kg ⋅ m2 / s2
1 J = 1 kg ⋅ m2 ⋅ s − 2 = 1 kg ⋅ m2 / s2

Care must be taken to apply the laws of exponents properly. Certain common problems are pointed out in the following examples.

EXAMPLE 5 Be careful with zero exponents

The expression ( − 5x)0( − 5x)0 equals 1, whereas the expression  − 5x0 − 5x0 equals  − 5. − 5. For ( − 5x)0 , ( − 5x)0 ,  the parentheses show that the expression  − 5x − 5x is raised to the zero power, whereas for  − 5x0 ,  − 5x0 ,  only x is raised to the zero power and we have

Negative 5 x to the power of 0 = negative 5 left parenthesis 1 right parenthesis = negative 5, where x to the power of 0 on left hand side points to 1 on the right hand side.

Also, ( − 5)0 = 1( − 5)0 = 1 but  − 50 =  − 1. − 50 =  − 1. Again, for ( − 5)0 , ( − 5)0 ,  parentheses show  − 5 − 5 raised to the zero power, whereas for  − 50 ,  − 50 ,  only 5 is raised to the zero power.

Similarly, comma left parenthesis negative 2 right parenthesis squared = 4 and negative 2 squared = negative 4. The negative operator on L H S point towards the negative operator on R H S. 2 squared on L H S point towards 4 on R H S.

For the same reasons comma 2 x to the power of negative 1 = 2 over x comma whereas left parenthesis 2 x right parenthesis negative 1 = 1 over 2 x.

EXAMPLE 6 Simplification done in different ways

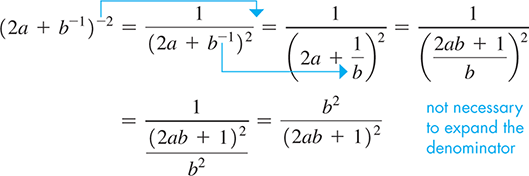
  1. Simplification of an expression, left parenthesis 2 a + b to the power of negative 1 right parenthesis to the power of negative 2 in 5 steps.

  2. (2a + b − 1) − 2 = (2a + 1b) − 2 = (2ab + 1b) − 2 = (2ab + 1) − 2b − 2 = b2(2ab + 1)2positive exponents usedin the final result(2a + b − 1) − 2 =  = (2a + 1b) − 2 = (2ab + 1b) − 2(2ab + 1) − 2b − 2 = b2(2ab + 1)2positive exponents usedin the final result

EXAMPLE 7 Be careful not to make a common error

There is an error that is commonly made in simplifying the type of expression in Example 6. We must be careful to see that

(2a + b − 1) − 2is not equal to(2a) − 2 + (b − 1) − 2 , or14a2 + b2
(2a + b − 1) − 2is not equal to(2a) − 2 + (b − 1) − 2 , or14a2 + b2

CAUTION

When raising a binomial (or any multinomial) to a power, we cannot simply raise each term to the power to obtain the result.

However, when raising a product of factors to a power, we use the equation (ab)n = anbn . (ab)n = anbn .  Thus,

(2ab − 1) − 2 = (2a) − 2(b − 1) − 2 = b2(2a)2 = b24a2
(2ab − 1) − 2 = (2a) − 2(b − 1) − 2 = b2(2a)2 = b24a2

We see that we must be careful to distinguish between the power of a sum of terms and the power of a product of factors.

CAUTION

From the preceding examples, we see that when a factor is moved from the denominator to the numerator of a fraction, or conversely, the sign of the exponent is changed. We should carefully note the word factor; this rule does not apply to moving terms in the numerator or the denominator.

EXAMPLE 8 Factor moved from numerator to denominator

Two examples, a and b illustrate factor moved from numerator to denominator

EXAMPLE 9 Simplifying a complex expression

Simplification of a complex expression, 1 over x to the power of negative 1 left parenthesis start fraction x to the power of negative 1 minus y to the power of negative 1, over x squared minus y squared end fraction right parenthesis in 7 steps.

CAUTION

Note that in this example, the x − 1x − 1 and y − 1y − 1 in the numerator could not be moved directly to the denominator with positive exponents because they are only terms of the original numerator, not factors.

EXAMPLE 10 Simplifying an expression from calculus

In finding out the rate at which a quantity is changing, it may be necessary to simplify an expression found by using the advanced mathematics of calculus. Simplify the following expression, which is derived using calculus.

3(x + 4)2(x − 3) − 2 − 2(x − 3) − 3(x + 4)3 = 3(x + 4)2(x − 3)2 − 2(x + 4)3(x − 3)3 = 3(x − 3)(x + 4)2 − 2(x + 4)3(x − 3)3 = (x + 4)2[ 3(x − 3) − 2(x + 4)] (x − 3)3 = (x + 4)2(x − 17)(x − 3)3
3(x + 4)2(x − 3) − 2 − 2(x − 3) − 3(x + 4)3 =  =  = 3(x + 4)2(x − 3)2 − 2(x + 4)3(x − 3)3 = 3(x − 3)(x + 4)2 − 2(x + 4)3(x − 3)3(x + 4)2[ 3(x − 3) − 2(x + 4)] (x − 3)3(x + 4)2(x − 17)(x − 3)3

Exercises 11.1

In Exercises 1–4, solve the resulting problems if the given changes are made in the indicated examples of this section.

  1. In Example 3, change the factor x2x2 to x − 2x − 2 and then find the result.

  2. In Example 6, change the term 2a to 2a–12a to 2a–1 and then find the result.

  3. In Example 8(b), change the 3 − 13 − 1 in the denominator to 3 − 23 − 2 and then find the result.

  4. In Example 9, change the sign in the numerator from  −  −  to  +  +  and then find the result.

In Exercises 5–56, express each of the given expressions in simplest form with only positive exponents.

  1. x8x − 3x8x − 3

  2. y9y − 2y9y − 2

  3. 2a2a − 62a2a − 6

  4. 5ss − 55ss − 5

  5. c7c − 2c7c − 2

  6. t − 8t − 3t − 8t − 3

  7. x5y − 2x5y − 2

  8. n − 6m − 4n − 6m − 4

  9. 50 × 5 − 350 × 5 − 3

  10. (32 × 4 − 3)3(32 × 4 − 3)3

  11. (2πx − 1)2(2πx − 1)2

  12. (3xy − 2)3(3xy − 2)3

  13. 2(5an − 2) − 12(5an − 2) − 1

  14. 4(6s2t − 1) − 24(6s2t − 1) − 2

  15. ( − 4)0( − 4)0

  16.  − 40 − 40

  17.  − 9x0 − 9x0

  18. ( − 7x)0( − 7x)0

  19. 3x − 23x − 2

  20. (3x) − 2(3x) − 2

  21. (7a − 1x) − 3(7a − 1x) − 3

  22. 7a − 1x − 37a − 1x − 3

  23. (2n3) − 4(2n3) − 4

  24. (x3 − 3) − 2(x3 − 3) − 2

  25. 3(ab − 2) − 33(ab − 2) − 3

  26. 5(2n − 2D − 1) − 25(2n − 2D − 1) − 2

  27. (a + b) − 1(a + b) − 1

  28. a − 1 + b − 1a − 1 + b − 1

  29. 2x − 3 + 4y − 22x − 3 + 4y − 2

  30. (3x − 2y) − 2(3x − 2y) − 2

  31. (2a − n)2(32an) − 1(2a − n)2(32an) − 1

  32. (7 × 3 − a)(3a7)2(7 × 3 − a)(3a7)2

  33. (3a24b) − 3(4a) − 5(3a24b) − 3(4a) − 5

  34. (2np − 2) − 2(4 − 1p2) − 1(2np − 2) − 2(4 − 1p2) − 1

  35. (V − 12t) − 2(t2V − 2) − 3(V − 12t) − 2(t2V − 2) − 3

  36. ab(a − 2b2) − 3(a − 3b5)2ab(a − 2b2) − 3(a − 3b5)2

  37. 3a − 2 + (3a − 2)43a − 2 + (3a − 2)4

  38. 3(a − 1z2) − 3 + c − 2z − 13(a − 1z2) − 3 + c − 2z − 1

  39. 2 × 3 − 1 + 4 × 3 − 22 × 3 − 1 + 4 × 3 − 2

  40. 5 × 8 − 2 − 3 − 1 × 235 × 8 − 2 − 3 − 1 × 23

  41. (R − 11 + R − 12) − 1(R − 11 + R − 12) − 1

  42. 6 − 2(2a − b − 2) − 16 − 2(2a − b − 2) − 1

  43. (n − 2 − 2n − 1)2(n − 2 − 2n − 1)2

  44. 2(3 − 3 − 9 − 1) − 22(3 − 3 − 9 − 1) − 2

  45. 6 − 14 − 2 + 26 − 14 − 2 + 2

  46. x − y − 1x − 1 − yx − y − 1x − 1 − y

  47. x − 2 − y − 2x − 1 − y − 1x − 2 − y − 2x − 1 − y − 1

  48. ax − 2 + a − 2xa − 1 + x − 1ax − 2 + a − 2xa − 1 + x − 1

  49. 2t − 2 + t − 1(t + 1)2t − 2 + t − 1(t + 1)

  50. 3x − 1 − x − 3(y + 2)3x − 1 − x − 3(y + 2)

  51. (D − 1) − 1 + (D + 1) − 1(D − 1) − 1 + (D + 1) − 1

  52. 4(2x − 1)(x + 2) − 1 − (2x − 1)2(x + 2) − 24(2x − 1)(x + 2) − 1 − (2x − 1)2(x + 2) − 2

In Exercises 57–78, solve the given problems.

  1. If x < 0 , x < 0 ,  is it ever true that x − 2 < x − 1 ? x − 2 < x − 1 ? 

  2. Is it true that (a + b)0 = 1(a + b)0 = 1 for all values of a and b?

  3. Express 42 × 6442 × 64 (a) as a power of 4 and (b) as a power of 2.

  4. Express 1/81 (a) as a power of 9 and (b) as a power of 3.

    1. By use of Eqs. (11.4) and (11.6), show that

      (ab) − n = (ba)n
      (ab) − n = (ba)n

    2. Verify the equation in part (a) by evaluating each side with a = 3.576 , b = 8.091 , a = 3.576 , b = 8.091 ,  and n = 7.n = 7.

  6. For what integer values of n is ( − 3) − n =  − 3 − n ? ( − 3) − n =  − 3 − n ?  Explain.

  7. For what integer value(s) of n is nπ > πn ? nπ > πn ? 

  8. Evaluate (819)12 / (816)14 . (819)12 / (816)14 .  What happens when you try to evaluate this on a calculator?

  9. Is it true that [  − 20 − ( − 1)0] 0 = 1 ? [  − 20 − ( − 1)0] 0 = 1 ? 

  10. Is it true that, if x ≠ 0 , [ ( − x − 2) − 2]  − 2 = 1 / x2 ? x ≠ 0 , [ ( − x − 2) − 2]  − 2 = 1 / x2 ? 

  11. If f(x) = 4x , f(x) = 4x ,  find f(a + 2) . f(a + 2) . 

  12. If f(x) = 2(9x) , f(x) = 2(9x) ,  find f(2 − a) . f(2 − a) . 

  13. Solve for x: 25x = 27(22x)2 . 25x = 27(22x)2 . 

  14. In analyzing the tuning of an electronic circuit, the expression [ ωω − 10 − ω0ω − 1] 2[ ωω − 10 − ω0ω − 1] 2 is used. Expand and simplify this expression.

  15. The metric unit of energy, the joule (J), can be expressed as kg  ⋅ s − 2 ⋅ m2 . kg  ⋅ s − 2 ⋅ m2 .  Simplify these units and include newtons (see Appendix B) and only positive exponents in the final result.

  16. The units for the electric quantity called permittivity are C2 ⋅ N − 1 ⋅ m − 2 . C2 ⋅ N − 1 ⋅ m − 2 .  Given that 1 F = 1 C2 ⋅ J − 1 , 1 F = 1 C2 ⋅ J − 1 ,  show that the units of permittivity are F/m. See Appendix B.

  17. When studying a solar energy system, the units encountered are kg ⋅ s − 1(m ⋅ s − 2)2 . kg ⋅ s − 1(m ⋅ s − 2)2 .  Simplify these units and include joules (see Exercise 71) and only positive exponents in the final result.

  18. The metric units for the velocity v of an object are m ⋅ s − 1 , m ⋅ s − 1 ,  and the units for the acceleration a of the object are m ⋅ s − 2 . m ⋅ s − 2 .  What are the units for v/a?

  19. Given that v = aptr , v = aptr ,  where v is the velocity of an object, a is its acceleration, and t is the time, use the metric units given in Exercise 74 to show that p = r = 1.p = r = 1.

  20. In optics, the combined focal length F of two lenses is given by F = [ f − 11 + f − 12 + d(f1f2) − 1]  − 1 , F = [ f − 11 + f − 12 + d(f1f2) − 1]  − 1 ,  where f1f1 and f2f2 are the focal lengths of the lenses and d is the distance between them. Simplify the right side of this equation.

  21. The monthly loan payment P for loan amount A with an annual interest rate r (as a decimal) for t years is

    P = A(r12)1 − (1 + r12) − 12 t
    P = A(r12)1 − (1 + r12) − 12 t

    Find the monthly payment for a $20,000 car loan if it is a 5-year loan with an annual interest rate of 4%.

  22. An idealized model of the thermodynamic process in a gasoline engine is the Otto cycle. The efficiency e of the process is

    e = T1rγr − T2rγr − T1 + T2T1rγr − T2rγr . Show thate = 1 − 1rγ − 1 . 
    e = T1rγr − T2rγr − T1 + T2T1rγr − T2rγr . Show thate = 1 − 1rγ − 1 . 

Answers to Practice Exercises

  1. ay6x2ay6x2

  2. x427x427

  3. 3

  4. a − 93a2a − 93a2

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.141.27.244