5.6 Solving Systems of Three Linear Equations in Three Unknowns by Determinants

  • Determinant of the Third Order • Cramer’s Rule • Solving Systems of Equations by Determinants • Determinants on the Calculator

Just as systems of two linear equations in two unknowns can be solved by determinants, so can systems of three linear equations in three unknowns. The system

a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3
(5.10)

can be solved in general terms by the method of elimination by addition or subtraction. This leads to the following solutions for x, y, and z.

x = d1b2c2 + d3b1c2 + d2b3c1 − d3b2c1 − d1b3c2 − d2b1c3a1b2c3 + a3b1c2 + a2b3c1 − a3b2c1 − a1b3c2 − a2b1c3y = a1d2c3 + a3d1c2 + a2d3c1 − a3d2c1 − a1d3c2 − a2d1c3a1b2c3 + a3b1c2 + a2b3c1 − a3b2c1 − a1b3c2 − a2b1c3z = a1b2d3 + a3b1d2 + a2b3d1 − a3b2d1 − a1b3d2 − a2b1d3a1b2c3 + a3b1c2 + a2b3c1 − a3b2c1 − a1b3c2 − a2b1c3
(5.11)

The expressions that appear in the numerators and denominators of Eqs. (5.11) are examples of a determinant of the third order. This determinant is defined by

 | a1b1c1a2b2c2a3b3c3 |  = a1b2c3 + a3b1c2 + a2b3c1 − a3b2c1 − a1b3c2 − a2b1c3
(5.12)

The elements, rows, columns, and diagonals of a third-order determinant are defined just as are those of a second-order determinant. For example, the principal diagonal is made up of the elements a1 ,  b2 ,  and c3 . 

Probably the easiest way of remembering the method of finding the value of a third-order determinant is as follows: Rewrite the first two columns to the right of the determinant. The products of the elements of the principal diagonal and the two parallel diagonals to the right of it are then added. The products of the elements of the secondary diagonal and the two parallel diagonals to the right of it are subtracted from the first sum. The algebraic sum of these six products gives the value of the determinant. These products are indicated in Fig. 5.46.

CAUTION

This method is used only for third-order determinants. It does not work for determinants of order higher than three.

A diagram of a third order determinant.

Fig. 5.46

Examples 1 and 2 illustrate this method of evaluating third-order determinants.

EXAMPLE 1 Evaluating a third-order determinant

A third-order determinant.

EXAMPLE 2 Evaluating a determinant with and without a calculator

A third-order determinant.

This determinant can also be evaluated on a calculator using the matrix feature. Figure 5.47 shows two windows for the determinant. The first shows the window for entering the numbers in the matrix. The second shows the matrix displayed and the evaluation of the determinant.

Two calculator screens.

Fig. 5.47

Inspection of Eqs. (5.11) reveals that the numerators of these solutions may also be written in terms of determinants. Thus, we may write the general solution to a system of three equations in three unknowns using determinants, which again is Cramer’s rule.

If the determinant of the denominator is not zero, there is a unique solution to the system of equations. If all determinants are zero, there is an unlimited number of solutions. If the determinant of the denominator is zero and any of the determinants of the numerators is not zero, the system is inconsistent, and there is no solution.

An analysis of Eqs. (5.13) shows that the situation is precisely the same as it was when we were using determinants to solve systems of two linear equations. That is,

  1. The determinants in the denominators are the same and are formed by using the coefficients of x, y, and z.

  2. The determinants in the numerators are the same as the one in the denominators except that the constant terms replace the column of coefficients of the unknown for which we are solving.

EXAMPLE 3 Solving a system using Cramer’s rule

Solve the following system by determinants.

3x + 2y − 5z =  − 12x − 3y − z = 115x − 2y + 7z = 9
Three equations. 3 x + 2 y minus 5 z = negative 1. 2 x minus 3 y minus z = 11 and 5 x minus 2 y + 7 z = 9 are solved using Cramer’s rule.

Substituting in each of the original equations shows that the solution checks:

3(2927) + 2( − 7727) − 5( − 827) = 87 − 154 + 4027 =  − 2727 =  − 12(2927) − 3( − 7727) − ( − 827) = 58 + 231 + 827 = 29727 = 115(2927) − 2( − 7727) + 7( − 827) = 145 + 154 − 5627 = 24327 = 9

After the values of x and y were determined, we could have evaluated z by substituting the values of x and y into one of the original equations.

EXAMPLE 4 Setting up and solving a system—mixing acid solutions

An 8.0% solution, an 11% solution, and an 18% solution of nitric acid are to be mixed to get 150 mL of a 12% solution. If the volume of acid from the 8.0% solution equals half the volume of acid from the other two solutions, how much of each is needed?

Let x = volume of 8.0% solution needed, y = volume of 11% solution needed, and z = volume of 18% solution needed.

The fact that the sum of the volumes of the three solutions is 150 mL leads to the equation x + y + z = 150 .  Because there are 0.080x mL of pure acid from the first solution, 0.11y mL from the second solution, and 0.18z mL from the third solution, and 0.12(150) mL in the final solution, we are led to the equation 0.080x + 0.11y + 0.18z = 18 .  Finally, using the last stated condition, we have the equation 0.080x = 0.5(0.11y + 0.18z) .  These equations are then written in the form of Eqs. (5.10) and solved.

acid in 8.0% solution       x +     y +     z = 1500.080x +  0.11y +  0.18z     =  180.080x                      = 0.05_ 5y + 0.090z       x +     y +     z = 1500.080x +  0.11y +  0.18z      =  180.080x − 0.055y − 0.090z   =    0            sum of volumes  volumes of pure acid     one-half of acid in others standard form of   Eqs. (5.10) by rewritingthird equation x =  | 15011180.110.180 − 0.055 − 0.090 | 1501180.110 − 0.055 | 1110.0800.110.180.080 − 0.055 − 0.090 | 110.0800.110.080 − 0.055 =  − 1.485 + 0 − 0.990 − 0 + 1.485 − 0 + 1.0800.0084 = 0.1800.0084 = 21Z =  | 111500.0800.11180.080 − 0.0550 | 110.0800.110.080 − 0.055                  the volue of z can also be found by    substituting x = 75 and y = 21into the first equation = 0 + 1.440 − 0.660 − 1.320 + 0.990 − 00.0084 = 0.4500.0084 = 54

Therefore, 75 mL of the 8.0% solution, 21 mL of the 11% solution, and 54 mL of the 18% solution are required to make the 12% solution. Results have been rounded off to two significant digits, the accuracy of the data. Checking with the statement of the problem, we see that these volumes total 150 mL.

Exercises 5.6

In Exercises 1 and 2, make the given change in the indicated examples of this section and then solve the resulting problems.

  1. In Example 1, interchange the first and second rows of the determinant and then evaluate it.

  2. In Example 3, change the constant to the right of the  =  sign in the first equation from  − 1 to  − 3 ,  change the constant to the right of the  =  sign in the third equation from 9 to 11, and then solve the resulting system of equations.

In Exercises 3–14, evaluate the given third-order determinants.

  1.  | 54 − 1 − 2 − 63711 | 

  2.  |  − 700245142 | 

  3.  | 89 − 6 − 3724 − 25 | 

  4.  |  − 24 − 15 − 144 − 82 | 

  5.  |  − 8 − 4 − 65 − 10210 − 1 | 

  6.  | 102 − 7 − 2 − 3665 − 2 | 

  7.  | 4 − 3 − 11 − 92 − 201 − 5 | 

  8.  | 9 − 20 − 13 − 6 − 4 − 6 − 2 | 

  9.  | 2018 − 50 − 1524 − 12 − 2055 − 22 | 

  10.  | 200 − 15 − 43016 − 140 | 

  11.  | 0.1 − 0.20 − 0.510.4 − 20.82 | 

  12.  | 0.25 − 0.54 − 0.421.200.350.28 − 0.500.12 − 0.44 | 

In Exercises 15–28, solve the given systems of equations by use of determinants. (Exercises 17–26 are the same as Exercises 3–12 of Section 5.5.)

  1. 2x + 3y + z = 43x − z =  − 3x − 2y + 2z =  − 5

  2. 4x + y + z = 22x − y − z = 43y + z = 2

  3. x + y + z = 2x − z = 1x + y = 1

  4. x + y − z =  − 3x + z = 22x − y + 2z = 3

  5. 2x + 3y + z = 2 − x + 2y + 3z =  − 1 − 3x − 3y + z = 0

  6. 2x + y − z = 44x − 3y − 2z =  − 28x − 2y − 3z = 3

  7. 5l + 6w − 3h = 64l − 7w − 2h =  − 33l + w − 7h = 1

  8. 3r + s − t = 2r + t − 2s = 04r − s + t = 3

  9. 2x − 2y + 3z = 52x + y − 2z =  − 13z + y − 4x = 0

  10. 2u + 2v + 3w = 03u + v + 4w = 21 − u − 3v + 7w = 15

  11. 3x − 7y + 3z = 63x + 3y + 6z = 15x − 5y + 2z = 5

  12. 18x + 24y +  4z = 4663x +  6y − 15z =  − 75 − 90x + 30y − 20z =  − 55

  13. p + 2q + 2r = 02p + 6q − 3r =  − 14p − 3q + 6r =  − 8

  14. 9x + 12y + 2z = 2321x + 2y − 5z =  − 256y − 18x − 4z =  − 11

The three points (x1 , y1) ,  (x2 , y2) ,  and (x3 , y3) are collinear (they lie on a single straight line) if  | x1y11x2y21x3y31 |  = 0 .  In Exercises 29 and 30, use this fact to decide if the given points are colliner.

  1. ( − 2 ,  1)(2 ,  3) ,  (6 ,  5)

  2. ( − 8 ,  20) ,  ( − 3 ,  6) ,  (1 ,  − 8)

In Exercises 31–34, use the determinant at the right. Answer the questions about the determinant for the changes given in each exercise.

 | 241365798 |  = 35

  1. How does the value change if the first two rows are interchanged?

  2. What is the value if the second row is replaced with the first row (the first row remains unchanged—the first and second rows are the same)?

  3. How does the value change if the elements of the first row are added to the corresponding elements of the second row (the first row remains unchanged)?

  4. How does value change if each element of the first row is multiplied by 2?

In Exercises 35–46, solve the given problems by determinants. In Exercises 40–46, set up appropriate systems of equations. All numbers are accurate to at least two significant digits.

  1. In analyzing the forces on the bell-crank mechanism shown in Fig. 5.49, the following equations are found. Find the forces.

    A robotic arm with forces at 3 points.

    Fig. 5.49

    A − 0.60F = 80B − 0.80F = 06.0A − 10F = 0

  2. 36. Using Kirchhoff’s laws (see the chapter introduction; the equations can be found in most physics textbooks) with the circuit shown in Fig. 5.50, the following equations are found. Find the indicated currents (in A) i1 ,  i2 ,  and i3 . 

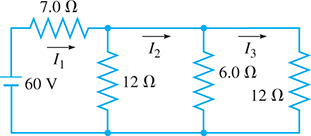
    A 60 volt circuit with current I sub 1 with 7.0 Ohms, I sub 2 with 12 Ohms, I sub 3 with 6.0 Ohms and 12 Ohms.

    Fig. 5.50

    19I1 − 12I2 = 6012I1 − 18I2 + 6.0I3 = 06.0I2 − 18I3 = 0

  3. In a laboratory experiment to measure the acceleration of an object, the distances traveled by the object were recorded for three different time intervals. These data led to the following equations:

    s0 + 2v0 +  2a = 20s0 + 4v0 +  8a = 54s0 + 6v0 + 18a = 104

    Here, s0 is the initial displacement (in ft), v0 is the initial velocity (in ft/s), and a is the acceleration (in ft / s2). Find s0 ,  v0 ,  and a.

  4. The angle θ between two links of a robot arm is given by θ = at3 + bt2 + ct ,  where t is the time during an 11.8-s cycle. If θ = 19.0 °  for t = 1.00 s ,   θ = 30.9 °  for t = 3.00 s ,  and θ = 19.8 °  for t = 5.00 s ,  find the equation θ = f(t) .  See Fig. 5.51.

    A robotic arm with angle theta between two links.

    Fig. 5.51

  5. The angles of a quadrilateral shaped parcel of land with two equal angles (see Fig. 5.52) have measures such that  ∠ A =  ∠ C +  ∠ B and  ∠ A + 2 ∠ B +  ∠ C = 280 °  .  Find the measures of these angles.

    A quadrilateral with angles Ay, Ay, B, and C.

    Fig. 5.52

  6. A certain 18-hole golf course has par-3, par-4, and par-5 holes, and there are twice as many par-4 holes as par-5 holes. How many holes of each type are there if a golfer has par on every hole for a score of 70?

  7. The increase L in length of a long metal rod is a function of the temperature T (in °C) given by L = a + bT + cT2 ,  where a, b, and c are constants. By evaluating a, b, and c, find L = f(T) ,  if L = 6.4 mm for T = 2.0 ° C ,  L  = 8.6 mm for T = 4.0 ° C ,  and V = 11.6 mm for T = 6.0 ° C . 

  8. An online retailer requires three different size containers to package its products for shipment. The costs of these containers, A, B, and C, and their capacities are shown as follows:

    Container A B C
    Cost ($ each) 4 6 7
    Capacity (in . 3) 200 400 600

    If the retailer orders 2500 containers with a total capacity of 1.1 × 106 in . 3 at a cost of $15,000, how many of each are in the order?

  9. An alloy used in electrical transformers contains nickel (Ni), iron (Fe), and molybdenum (Mo). The percent of Ni is 1% less than five times the percent of Fe. The percent of Fe is 1% more than three times the percent of Mo. Find the percent of each in the alloy.

  10. A company budgets $750,000 in salaries, hardware, and computer time for the design of a new product. The salaries are as much as the others combined, and the hardware budget is twice the computer budget. How much is budgeted for each?

  11. A person spent 1.10 h in a car going to an airport, 1.95 h flying in a jet, and 0.520 h in a taxi to reach the final destination. The jet’s speed averaged 12.0 times that of the car, which averaged 15.0 mi/h more than the taxi. What was the average speed of each if the trip covered 1140 mi?

  12. An intravenous aqueous solution is made from three mixtures to get 500 mL with 6.0% of one medication, 8.0% of a second medication, and 86% water. The percents in the mixtures are, respectively, 5.0, 20, 75 (first), 0, 5.0, 95 (second), and 10, 5.0, 85 (third). How much of each is used?

Answers to Practice Exercises

  1. 38

  2. 38

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.119.143.4