Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

13.3 Properties of Logarithms

Sum of Logarithms for Product • Difference of Logarithms for Quotient • Multiple of Logarithm for Power • Logarithms of 1 and b

Because a logarithm is an exponent, it must follow the laws of exponents. The laws used in this section to derive the very useful properties of logarithms are listed here for reference.

b^{u} b^{v} = b^{u + v}

$b^{u} b^{v} = b^{u + v}$ (13.4)

\frac{b^{u}}{b^{v}} = b^{u - v}

$\frac{b^{u}}{b^{v}} = b^{u - v}$ (13.5)

{(b^{u})}^{n} = b^{n u}

${(b^{u})}^{n} = b^{n u}$ (13.6)

The next example shows the reasoning used in deriving the properties of logarithms.

EXAMPLE 1 Sum of logarithms for product

We know that $8 \times 16 = 128.$ $8 \times 16 = 128.$ Writing these numbers as powers of 2, we have

8 = 2^{3} 16 = 2^{4} 128 = 2^{7} = 2^{3 + 4}

$8 = 2^{3} 16 = 2^{4} 128 = 2^{7} = 2^{3 + 4}$

The logarithmic forms can be written as

3 = \log_{2} 8 4 = \log_{2} 16 3 + 4 = \log_{2} 128

$3 = \log_{2} 8 4 = \log_{2} 16 3 + 4 = \log_{2} 128$

This means that

\log_{2} 8 + \log_{2} 16 = \log_{2} 128

$\log_{2} 8 + \log_{2} 16 = \log_{2} 128$

where

8 \times 16 = 128

$8 \times 16 = 128$

The sum of the logarithms of 8 and 16 equals the logarithm of 128, where the product of 8 and 16 equals 128.

Following Example 1, if we let $u = \log_{b} x$ $u = \log_{b} x$ and $v = \log_{b} y$ $v = \log_{b} y$ and write these equations in exponential form, we have $x = b^{u}$ $x = b^{u}$ and $y = b^{v} .$ $y = b^{v} .$ Therefore, forming the product of x and y, we obtain

\begin{array}{l} x y = b^{u} b^{v} = b^{u + v} & or & x y = b^{u + v} \end{array}

$\begin{array}{l} x y = b^{u} b^{v} = b^{u + v} & or & x y = b^{u + v} \end{array}$

Writing this last equation in logarithmic form yields

u + v = \log_{b} x y

$u + v = \log_{b} x y$

This means that the logarithm of a product can be written as

\log_{b} x y = \log_{b} x + \log_{b} y

$\log_{b} x y = \log_{b} x + \log_{b} y$ (13.7)

Equation (13.7) states the property that the logarithm of the product of two numbers is equal to the sum of the logarithms of the numbers.

Using the same definitions of u and v to form the quotient of x and y, we then have

\frac{x}{y} = \frac{b^{u}}{b^{v}} = b^{u - v} or \frac{x}{y} = b^{u - v}

$\frac{x}{y} = \frac{b^{u}}{b^{v}} = b^{u - v} or \frac{x}{y} = b^{u - v}$

Writing this last equation in logarithmic form, we have

u - v = \log_{b} (\frac{x}{y}) .

$u - v = \log_{b} (\frac{x}{y}) .$

Therefore, the logarithm of a quotient is given by

\log_{b} (\frac{x}{y}) = \log_{b} x - \log_{b} y

$\log_{b} (\frac{x}{y}) = \log_{b} x - \log_{b} y$ (13.8)

Equation (13.8) states the property that the logarithm of the quotient of two numbers is equal to the logarithm of the numerator minus the logarithm of the denominator.

CAUTION

Noting Equations (13.7) and (13.8), it is very clear that

\begin{array}{l} \log x + \log y & is not equal to & \log (x + y) \\ \log x - \log y & is not equal to & \log (x - y) \end{array}

$\begin{array}{l} \log x + \log y & is not equal to & \log (x + y) \\ \log x - \log y & is not equal to & \log (x - y) \end{array}$

If we again let $u = \log_{b} x$ $u = \log_{b} x$ and write this in exponential form, we have $x = b^{u} .$ $x = b^{u} .$ To find the nth power of x, we write

x^{n} = {(b^{u})}^{n} = b^{n u}

$x^{n} = {(b^{u})}^{n} = b^{n u}$

Expressing this equation in logarithmic form yields

n u = \log_{b} (x^{n}) .

$n u = \log_{b} (x^{n}) .$

Thus, the logarithm of a power is given by

\log_{b} (x^{n}) = n \log_{b} x

$\log_{b} (x^{n}) = n \log_{b} x$ (13.9)

Equation (13.9) states that the logarithm of the nth power of a number is equal to n times the logarithm of the number. The exponent n may be any real number, which, of course, includes all rational and irrational numbers.

In Section 13.2, we showed that the base b of logarithms must be a positive number. Because $x = b^{u}$ $x = b^{u}$ and $y = b^{v},$ $y = b^{v},$ this means that x and y are also positive numbers. Therefore, the properties of logarithms that have just been derived are valid only for positive values of x and y.

EXAMPLE 2 Logarithms of product, quotient, power

Using Eq. (13.7), we may express $\log_{4}$ $\log_{4}$ 15 as a sum of logarithms:
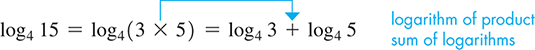
Using Eq. (13.8), we may express $\log_{4} (\frac{5}{3})$ $\log_{4} (\frac{5}{3})$ as the difference of logarithms:
Using Eq. (13.9), we may express $\log_{4} (t^{2})$ $\log_{4} (t^{2})$ as twice $\log_{4} t :$ $\log_{4} t :$

$\begin{array}{l} \log_{4} (t^{2}) = 2 \log_{4} t & \begin{array}{l} logarithm of power \\ multiple of logarithm \end{array} \end{array}$ $\begin{array}{l} \log_{4} (t^{2}) = 2 \log_{4} t & \begin{array}{l} logarithm of power \\ multiple of logarithm \end{array} \end{array}$
Using Eq. (13.8) and then Eq. (13.7), we have

$\begin{array}{rcl} \log_{4} (\frac{x y}{z}) & = & \log_{4} (x y) - \log_{4} z \\ = & \log_{4} x + \log_{4} y - \log_{4} z \end{array}$ $\begin{array}{rcl} \log_{4} (\frac{x y}{z}) & = & \log_{4} (x y) - \log_{4} z \\ = & \log_{4} x + \log_{4} y - \log_{4} z \end{array}$

EXAMPLE 3 Sum or difference of logarithms as a single quantity

We may also express a sum or difference of logarithms as the logarithm of a single quantity.

$\begin{array}{l} \log_{4} 3 + \log_{4} x = \log_{4} (3 \times x) = \log_{4} 3 x & using Eq . (13.7) \end{array}$ $\begin{array}{l} \log_{4} 3 + \log_{4} x = \log_{4} (3 \times x) = \log_{4} 3 x & using Eq . (13.7) \end{array}$
$\begin{array}{l} \log_{4} 3 - \log_{4} x = \log_{4} (\frac{3}{x}) & using Eq . (13.8) \end{array}$ $\begin{array}{l} \log_{4} 3 - \log_{4} x = \log_{4} (\frac{3}{x}) & using Eq . (13.8) \end{array}$
$\begin{array}{l} \log_{4} 3 + 2 \log_{4} x = \log_{4} 3 + \log_{4} (x^{2}) = \log_{4} 3 x^{2} & using Eqs . (13.7) and (13.9) \end{array}$ $\begin{array}{l} \log_{4} 3 + 2 \log_{4} x = \log_{4} 3 + \log_{4} (x^{2}) = \log_{4} 3 x^{2} & using Eqs . (13.7) and (13.9) \end{array}$
$\begin{array}{l} \log_{4} 3 + 2 \log_{4} x - \log_{4} y = \log_{4} (\frac{3 x^{2}}{y}) & using Eqs . (13.7), (13.8), and (13.9) \end{array}$ $\begin{array}{l} \log_{4} 3 + 2 \log_{4} x - \log_{4} y = \log_{4} (\frac{3 x^{2}}{y}) & using Eqs . (13.7), (13.8), and (13.9) \end{array}$

In Section 13.2, we noted that $\log_{b} 1 = 0.$ $\log_{b} 1 = 0.$ Also, because $b = b^{1}$ $b = b^{1}$ in logarithmic form is $\log_{b} b = 1,$ $\log_{b} b = 1,$ we have $\log_{b} (b^{x}) = x \log_{b} b = x (1) = x .$ $\log_{b} (b^{x}) = x \log_{b} b = x (1) = x .$ In addition, the logarithmic form of $\log_{b} x = \log_{b} x$ $\log_{b} x = \log_{b} x$ is $b^{\log_{b} x} = x .$ $b^{\log_{b} x} = x .$

Summarizing these properties, we have

\log_{b} 1 = 0 \log_{b} b = 1

$\log_{b} 1 = 0 \log_{b} b = 1$ (13.10)

\log_{b} (b^{x}) = x

$\log_{b} (b^{x}) = x$ (13.11)

b^{\log_{b} x} = x

$b^{\log_{b} x} = x$ (13.12)

These equations can be used to simplify certain expressions.

EXAMPLE 4 Exact values for certain logarithms

We may evaluate $\log_{3} 9$ $\log_{3} 9$ using Eq. (13.11):

$\log_{3} 9 = \log_{3} (3^{2}) = 2$ $\log_{3} 9 = \log_{3} (3^{2}) = 2$

We can establish the exact value since the base of logarithms and the number being raised to the power are the same. Of course, this could have been evaluated directly from the definition of a logarithm.
Using Eq. (13.11), we can write $\log_{3} (3^{0.4}) = 0.4.$ $\log_{3} (3^{0.4}) = 0.4.$ Although we did not evaluate $3^{0.4},$ $3^{0.4},$ we can evaluate $\log_{3} (3^{0.4}) .$ $\log_{3} (3^{0.4}) .$

EXAMPLE 5 Using the properties of logarithms

$\log_{2} 6 = \log_{2} (2 \times 3) = \log_{2} 2 + \log_{2} 3 = 1 + \log_{2} 3$ $\log_{2} 6 = \log_{2} (2 \times 3) = \log_{2} 2 + \log_{2} 3 = 1 + \log_{2} 3$
$\log_{5} \frac{1}{5} = \log_{5} 1 - \log_{5} 5 = 0 - 1 = - 1$ $\log_{5} \frac{1}{5} = \log_{5} 1 - \log_{5} 5 = 0 - 1 = - 1$
$\log_{7} \sqrt{7} = \log_{7} (7^{1/2}) = \frac{1}{2} \log_{7} 7 = \frac{1}{2}$ $\log_{7} \sqrt{7} = \log_{7} (7^{1/2}) = \frac{1}{2} \log_{7} 7 = \frac{1}{2}$
$3^{\log_{3} 8} + 4^{\log_{4} 7} = 8 + 7 = 15$ $3^{\log_{3} 8} + 4^{\log_{4} 7} = 8 + 7 = 15$

EXAMPLE 6 Evaluation in two ways

The following illustration shows the evaluation of a logarithm in two different ways. Either method is appropriate.

$\log_{5} (\frac{1}{25}) = \log_{5} 1 - \log_{5} 25 = 0 - \log_{5} (5^{2}) = - 2$ $\log_{5} (\frac{1}{25}) = \log_{5} 1 - \log_{5} 25 = 0 - \log_{5} (5^{2}) = - 2$
$\log_{5} (\frac{1}{25}) = \log_{5} (5^{- 2}) = - 2$ $\log_{5} (\frac{1}{25}) = \log_{5} (5^{- 2}) = - 2$

EXAMPLE 7 Solving equation with logarithms

Use the basic properties of logarithms to solve the following equation for y in terms of x: $\log_{b} y = 2 \log_{b} x + \log_{b} a .$ $\log_{b} y = 2 \log_{b} x + \log_{b} a .$

Using Eq. (13.9) and then Eq. (13.7), we have

\log_{b} y = \log_{b} (x^{2}) + \log_{b} a = \log_{b} (a x^{2})

$\log_{b} y = \log_{b} (x^{2}) + \log_{b} a = \log_{b} (a x^{2})$

Because we have the logarithm to the base b of different expressions on each side of the resulting equation, the expressions must be equal. Therefore,

y = a x^{2}

$y = a x^{2}$

EXAMPLE 8 Solving equation—radioactive decay

An equation encountered in the study of radioactive elements is $\log_{e} N - \log_{e} N_{0} = k t .$ $\log_{e} N - \log_{e} N_{0} = k t .$ Here, N is the amount of the element present at any time t, and $N_{0}$ $N_{0}$ is the original amount. Solve for N as a function of t.

Using Eq. (13.8), we rewrite the left side of this equation, obtaining

\log_{e} (\frac{N}{N_{0}}) = k t

$\log_{e} (\frac{N}{N_{0}}) = k t$

Rewriting this in exponential form, we have

\frac{N}{N_{0}} = e^{k t}, or N = N_{0} e^{k t}

$\frac{N}{N_{0}} = e^{k t}, or N = N_{0} e^{k t}$

EXERCISES 13.3

In Exercises 1–8, perform the indicated operations on the resulting expressions if the given changes are made in the original expressions of the indicated examples of this section.

In Example 2(a), change the 15 to 21.
In Example 2(d), change the x to 2 and the z to 3.
In Example 3(b), change the 3 to 5.
In Example 3(c), change the 2 to 3.
In Example 4(a), change the 9 to 27.
In Example 5(a), change the 6 to 10.
In Example 5(c), change the 7’s to 5’s.
In Example 7, change the 2 to 3.

In Exercises 9–20, express each as a sum, difference, or multiple of logarithms. See Example 2.

$\log_{5} 33$ $\log_{5} 33$
$\log_{3} 14$ $\log_{3} 14$
$\log_{7} (\frac{9}{2})$ $\log_{7} (\frac{9}{2})$
$\log_{3} (\frac{2}{11})$ $\log_{3} (\frac{2}{11})$
$\log_{2} (a^{3})$ $\log_{2} (a^{3})$
$2 \log_{8} (n^{5})$ $2 \log_{8} (n^{5})$
$\log_{6} (a b c^{2})$ $\log_{6} (a b c^{2})$
$\log_{2} (\frac{x y}{z^{2}})$ $\log_{2} (\frac{x y}{z^{2}})$
$10 \log_{5} \sqrt{t}$ $10 \log_{5} \sqrt{t}$
$\log_{4} \sqrt[7]{x}$ $\log_{4} \sqrt[7]{x}$
$\log_{2} (\frac{\sqrt{x}}{a^{2}})$ $\log_{2} (\frac{\sqrt{x}}{a^{2}})$
${log}_{3} (\frac{\sqrt[3]{y}}{7 x})$ ${log}_{3} (\frac{\sqrt[3]{y}}{7 x})$

In Exercises 21–28, express each as the logarithm of a single quantity. See Example 3.

$\log_{b} a + \log_{b} c$ $\log_{b} a + \log_{b} c$
$\log_{2} 3 + \log_{2} x$ $\log_{2} 3 + \log_{2} x$
$\log_{5} 9 - \log_{5} 3$ $\log_{5} 9 - \log_{5} 3$
$- \log_{8} R + \log_{8} V$ $- \log_{8} R + \log_{8} V$
$\log_{b} \sqrt{x} + \log_{b} x^{2}$ $\log_{b} \sqrt{x} + \log_{b} x^{2}$
$\log_{4} 3^{3} + \log_{4} 9$ $\log_{4} 3^{3} + \log_{4} 9$
$2 \log_{e} 2 + 3 \log_{e} π - \log_{e} 3$ $2 \log_{e} 2 + 3 \log_{e} π - \log_{e} 3$
$\frac{1}{2} \log_{b} a - 2 \log_{b} 5 - 3 \log_{b} x$ $\frac{1}{2} \log_{b} a - 2 \log_{b} 5 - 3 \log_{b} x$

In Exercises 29–36, determine the exact value of each of the given expressions.

$\log_{2} (\frac{1}{32})$ $\log_{2} (\frac{1}{32})$
$\log_{3} (\frac{2}{162})$ $\log_{3} (\frac{2}{162})$
$\log_{2} (2^{2.5})$ $\log_{2} (2^{2.5})$
$\log_{5} (5^{0.1})$ $\log_{5} (5^{0.1})$
$6 \log_{7} \sqrt{7}$ $6 \log_{7} \sqrt{7}$
$π {log}_{6} \sqrt[3]{6}$ $π {log}_{6} \sqrt[3]{6}$
$4^{\log_{4} 8}$ $4^{\log_{4} 8}$
$10^{2 \log_{10} 3}$ $10^{2 \log_{10} 3}$

In Exercises 37–44, express each as a sum, difference, or multiple of logarithms. In each case, part of the logarithm may be determined exactly.

$\log_{3} 18$ $\log_{3} 18$
$\log_{5} 375$ $\log_{5} 375$
$\log_{2} (\frac{4}{7})$ $\log_{2} (\frac{4}{7})$
$\log_{10} (0.05)$ $\log_{10} (0.05)$
$\log_{3} \sqrt{6}$ $\log_{3} \sqrt{6}$
$\log_{2} \sqrt[3]{24}$ $\log_{2} \sqrt[3]{24}$
$\log_{10} 3000$ $\log_{10} 3000$
$3 \log_{10} (40^{2})$ $3 \log_{10} (40^{2})$

In Exercises 45–56, solve for y in terms of x.

$\log_{b} y = \log_{b} 2 + \log_{b} x$ $\log_{b} y = \log_{b} 2 + \log_{b} x$
$\log_{b} y = \log_{b} 6 - \log_{b} x$ $\log_{b} y = \log_{b} 6 - \log_{b} x$
$\log_{4} y = \log_{4} x - \log_{4} 10 + \log_{4} 6$ $\log_{4} y = \log_{4} x - \log_{4} 10 + \log_{4} 6$
$\log_{3} y = - 2 \log_{3} (x + 1) + \log_{3} 7$ $\log_{3} y = - 2 \log_{3} (x + 1) + \log_{3} 7$
$\log_{10} y = 2 \log_{10} 7 - 3 \log_{10} x$ $\log_{10} y = 2 \log_{10} 7 - 3 \log_{10} x$
$\log_{b} y = 3 \log_{b} \sqrt{x} + 2 \log_{b} 10$ $\log_{b} y = 3 \log_{b} \sqrt{x} + 2 \log_{b} 10$
$5 \log_{2} y - \log_{2} x = 3 \log_{2} 4 + \log_{2} a$ $5 \log_{2} y - \log_{2} x = 3 \log_{2} 4 + \log_{2} a$
$4 \log_{2} x - 3 \log_{2} y = \log_{2} 27$ $4 \log_{2} x - 3 \log_{2} y = \log_{2} 27$
$\log_{2} x + \log_{2} y = 1$ $\log_{2} x + \log_{2} y = 1$
$π \log_{4} x + \log_{4} y = 1$ $π \log_{4} x + \log_{4} y = 1$
$2 \log_{5} x - \log_{5} y = 2$ $2 \log_{5} x - \log_{5} y = 2$
$\log_{8} x = 2 \log_{8} y + 4$ $\log_{8} x = 2 \log_{8} y + 4$

In Exercises 57–70, solve the given problems.

Explain why $\log_{10} (x + 3)$ $\log_{10} (x + 3)$ is not equal to $\log_{10} x + \log_{10} 3.$ $\log_{10} x + \log_{10} 3.$
Express as the logarithm of a single quantity: $2 \log_{2} (2 x) - \log_{2} x^{2} .$ $2 \log_{2} (2 x) - \log_{2} x^{2} .$ For what values of x is the value of this expression valid? Explain.
Display the graphs of $y = \log_{e} (e^{2} x)$ $y = \log_{e} (e^{2} x)$ and $y = 2 + \log_{e} x$ $y = 2 + \log_{e} x$ on a calculator and explain why they are the same.
If $x = \log_{b} 2$ $x = \log_{b} 2$ and $y = \log_{b} 3,$ $y = \log_{b} 3,$ express $\log_{b} 12$ $\log_{b} 12$ in terms of x and y.
If $\log_{b} x = 2$ $\log_{b} x = 2$ and $\log_{b} y = 3,$ $\log_{b} y = 3,$ find $\log_{b} \sqrt{x^{2} y^{4}} .$ $\log_{b} \sqrt{x^{2} y^{4}} .$
Is it true that $\log_{b} {(a b)}^{x} = x \log_{b} a + x ?$ $\log_{b} {(a b)}^{x} = x \log_{b} a + x ?$
Simplify: $\log_{b} (1 + b^{2 x}) - \log_{b} (1 + b^{- 2 x})$ $\log_{b} (1 + b^{2 x}) - \log_{b} (1 + b^{- 2 x})$
If $f (x) = \log_{b} x,$ $f (x) = \log_{b} x,$ express $\frac{f (x + h) - f (x)}{h}$ $\frac{f (x + h) - f (x)}{h}$ as a single logarithm.
On the same screen of a calculator, display the graphs of $y_{1} = \log_{10} x - \log_{10} (x^{2} + 1)$ $y_{1} = \log_{10} x - \log_{10} (x^{2} + 1)$ and $y_{2} = \log_{10} \frac{x}{x^{2} + 1} .$ $y_{2} = \log_{10} \frac{x}{x^{2} + 1} .$ What conclusion can be drawn from the display?
The use of the insecticide DDT was banned in the United States in 1972. A computer analysis shows that an expression relating the amount A still present in an area, the original amount $A_{0},$ $A_{0},$ and the time t (in years) since 1972 is $\log_{10} A = \log_{10} A_{0} + 0.1 t \log_{10} 0.8.$ $\log_{10} A = \log_{10} A_{0} + 0.1 t \log_{10} 0.8.$ Solve for A as a function of t.
A study of urban density shows that the population density D (in $persons / {mi}^{2}$ $persons / {mi}^{2}$ ) is related to the distance r (in mi) from the city center by $\log_{e} D = \log_{e} a - b r + c r^{2},$ $\log_{e} D = \log_{e} a - b r + c r^{2},$ where a, b, and c are positive constants. Solve for D as a function of r.
When a person ingests a medication capsule, it is found that the rate R (in mg/min) that it enters the bloodstream in time t (in min) is given by $\log_{10} R - \log_{10} 5 = t \log_{10} 0.95.$ $\log_{10} R - \log_{10} 5 = t \log_{10} 0.95.$ Solve for R as a function of t.
A container of water is heated to 90°C and then placed in a room at 0°C. The temperature T of the water is related to the time t (in min) by $\log_{e} T = \log_{e} 90.0 - 0.23 t .$ $\log_{e} T = \log_{e} 90.0 - 0.23 t .$ Find T as a function of t.
In analyzing the power gain in a microprocessor circuit, the equation $N = 10 (2 \log_{10} I_{1} - 2 \log_{10} I_{2} + \log_{10} R_{1} - \log_{10} R_{2})$ $N = 10 (2 \log_{10} I_{1} - 2 \log_{10} I_{2} + \log_{10} R_{1} - \log_{10} R_{2})$ is used. Express this with a single logarithm on the right side.

Answers to Practice Exercises

$\log_{3} 2 + \log_{3} 5$ $\log_{3} 2 + \log_{3} 5$
$\log_{3} 2 + \log_{3} a - \log_{3} 5$ $\log_{3} 2 + \log_{3} a - \log_{3} 5$
$\log_{4} (5 / x^{3})$ $\log_{4} (5 / x^{3})$
6

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 13.3 Properties of Logarithms

Create new playlist

Sign In

Sign Up

Table of Contents for
13.3 Properties of Logarithms