15.1 The Remainder and Factor Theorems; Synthetic Division

  • Polynomial Function • Remainder Theorem • Factor Theorem • Synthetic Division

In solving higher-degree polynomial equations, the quadratic formula can be used for second-degree equations, and methods have been found for certain third- and fourth-degree equations. It can also be proven that polynomial equations of degree higher than 4 cannot in general be solved algebraically.

In this section, we present two theorems and a simplified method for algebraic division. These will help us in solving polynomial equations later in the chapter.

Any function of the form

f(x) = anxn + an  −  1xn − 1 +  ⋯  + a0
f(x) = anxn + an  −  1xn − 1 +  ⋯  + a0
(15.1)

where an ≠ 0an ≠ 0 and n is a positive integer or zero is called a polynomial function. We will be considering only polynomials in which the coefficients a0 , a1 ,   …  ,  ana0 , a1 ,   …  ,  an are real numbers.

If we divide a polynomial by x − r ,  x − r ,   we find a result of the form

f(x) = (x − r)q(x) + R
f(x) = (x − r)q(x) + R
(15.2)

where q(x) is the quotient and R is the remainder.

EXAMPLE 1 Division with remainder

Divide f(x) = 3x2 + 5x − 8f(x) = 3x2 + 5x − 8 by x − 2.x − 2.

The division is shown at the left, and it shows that

3x2 + 5x − 8 = (x − 2)(3x + 11) + 14
3x2 + 5x − 8 = (x − 2)(3x + 11) + 14

where, for this function f(x) with r = 2 ,  r = 2 ,   we identify q(x) and R as

q(x) = 3x + 11R = 14
q(x) = 3x + 11R = 14

THE REMAINDER THEOREM

If we now set x = rx = r in Eq. (15.2), we have f(r) = q(r)(r − r) + R = q(r)(0) + R , f(r) = q(r)(r − r) + R = q(r)(0) + R ,  or

f(r) = R
f(r) = R
(15.3)

This leads us to the remainder theorem, which is stated below.

This means the remainder equals the value of the function at x = r . x = r . 

EXAMPLE 2 Verifying the remainder theorem

In Example 1, f(x) = 3x2 + 5x − 8 ,  R = 14 , f(x) = 3x2 + 5x − 8 ,  R = 14 ,  and r = 2.r = 2.

We find that

f(2) = 3(22) + 5(2) − 8 = 12 + 10 − 8 = 14
f(2) =  =  = 3(22) + 5(2) − 812 + 10 − 814

Therefore, f(2) = 14f(2) = 14 verifies that f(r) = Rf(r) = R for this example.

EXAMPLE 3 Using the remainder theorem

By using the remainder theorem, determine the remainder when 3x3 − x2 − 20x + 53x3 − x2 − 20x + 5 is divided by x + 4.x + 4.

In using the remainder theorem, we determine the remainder when the function is divided by x − rx − r by evaluating the function for x = r . x = r .  To have x + 4x + 4 in the proper form to identify r, we write it as x − ( − 4) . x − ( − 4) .  This means that r =  − 4 , r =  − 4 ,  and we therefore evaluate the function f(x) = 3x3 − x2 − 20x + 5f(x) = 3x3 − x2 − 20x + 5 for x =  − 4 , x =  − 4 ,  or find f( − 4) : f( − 4) : 

f( − 4) = 3( − 4)3 − ( − 4)2 − 20( − 4) + 5 =  − 192 − 16 + 80 + 5 =  − 123
f( − 4) =  = 3( − 4)3 − ( − 4)2 − 20( − 4) + 5 =  − 192 − 16 + 80 + 5 − 123

The remainder is  − 123 − 123 when 3x3 − x2 − 20x + 53x3 − x2 − 20x + 5 is divided by x + 4.x + 4.

THE FACTOR THEOREM

The remainder theorem leads to another important theorem known as the factor theorem. It states that if f(r) = R = 0 , f(r) = R = 0 ,  then x − rx − r is a factor of f(x). We see in Eq. (15.2) that if the remainder R = 0 , R = 0 ,  then f(x) = (x − r)q(x) , f(x) = (x − r)q(x) ,  and this shows that x − rx − r is a factor of f(x). Therefore, we have the following meanings for f(r) = 0.f(r) = 0.

EXAMPLE 4 Using the factor theorem

  1. We determine that t + 1t + 1 is a factor of f(t) = t3 + 2t2 − 5t − 6f(t) = t3 + 2t2 − 5t − 6 because f( − 1) = 0 , f( − 1) = 0 ,  as we now show:

    f( − 1) = ( − 1)3 + 2( − 1)2 − 5( − 1) − 6 =  − 1 + 2 + 5 − 6 = 0
    f( − 1) = ( − 1)3 + 2( − 1)2 − 5( − 1) − 6 =  − 1 + 2 + 5 − 6 = 0

  2. However, t + 2t + 2 is not a factor of f(t) because f( − 2)f( − 2) is not zero, as we now show:

    f( − 2) = ( − 2)3 + 2( − 2)2 − 5( − 2) − 6 =  − 8 + 8 + 10 − 6 = 4
    f( − 2) = ( − 2)3 + 2( − 2)2 − 5( − 2) − 6 =  − 8 + 8 + 10 − 6 = 4

SYNTHETIC DIVISION

In the sections that follow, we will find that division of a polynomial by the factor x − rx − r is also useful in solving polynomial equations. Therefore, we now develop a simplified form of long division, known as synthetic division. It allows us to easily find the coefficients of the quotient and the remainder. If the degree of the equation is high, it is easier to use synthetic division than to calculate f(r). The method for synthetic division is developed in the following example.

EXAMPLE 5 Developing synthetic division

Divide x4 + 4x3 − x2 − 16x − 14x4 + 4x3 − x2 − 16x − 14 by x − 2 . x − 2 . 

We first perform this division in the usual manner:

x3 + 6x2 + 11x + 6x − 2_ x4 + 4x3 − x2 − 16x − 14x4 − 2x3_ 6x3 − x26x3 − 12x2_ 11x2 − 16x11x2 − 22x_ 6x − 146x − 12_  − 2
x3 + 6x2 + 11x + 6x − 2_ x4 + 4x3 − x2 − 16x − 14x4 − 2x3_ 6x3 − x26x3 − 12x2_ 11x2 − 16x11x2 − 22x_ 6x − 146x − 12_  − 2

In doing the division, notice that we repeat many terms and that the only important numbers are the coefficients. This means there is no need to write in the powers of x. To the left of the division, we write it without x’s and without identical terms.

All numbers below the dividend may be written in two lines. Then all coefficients of the quotient, except the first, appear in the bottom line. Therefore, the line above the dividend is omitted, and we have the form at the left.

Now, write the first coefficient (in this case, 1) in the bottom line. Also, change the  − 2 − 2 to 2, which is the actual value of r. Then in the form at the left, write the 2 on the right. In this form, the 1, 6, 11, and 6 are the coefficients of the x3 ,  x2 , x3 ,  x2 ,  x, and constant term of the quotient. The  − 2 − 2 is the remainder.

Finally, it is easier to use addition rather than subtraction in the process, so we change the signs of the numbers in the middle row. Remember that originally the bottom line was found by subtraction. Therefore, we have the last form on the left.

In the last form at the left, we have 1(of the bottom row) × 2( = r) = 2 , 1(of the bottom row) × 2( = r) = 2 ,  the first number of the middle row. In the second column, 4 + 2 = 6 , 4 + 2 = 6 ,  the second number in the bottom row. Then, 6 × 2( = r) = 12 , 6 × 2( = r) = 12 ,  the second number of the second row;  − 1 + 12 = 11 ;  11 × 2 = 22 ;  22 + ( − 16) = 6 ;  6 × 2 = 12 ;  − 1 + 12 = 11 ;  11 × 2 = 22 ;  22 + ( − 16) = 6 ;  6 × 2 = 12 ;  and 12 + ( − 14) =  − 2 . 12 + ( − 14) =  − 2 . 

We read the bottom line of the last form, the one we use in synthetic division, as

1x3 + 6x2 + 11x + 6 with a remainder of  − 2
1x3 + 6x2 + 11x + 6 with a remainder of  − 2

The method of synthetic division shown in the last form is outlined below.

Using synthetic division, the last number in the bottom row is the remainder, and the other numbers are the respective coefficients of the quotient. The first term of the quotient is of degree one less than the first term of the dividend.

EXAMPLE 6 Using synthetic division

Divide x5 + 2x4 − 4x2 + 3x − 4x5 + 2x4 − 4x2 + 3x − 4 by x + 3x + 3 using synthetic division.

Because the powers of x are in descending order, write down the coefficients of f(x). In doing so, we must be certain to include a zero for the missing x3x3 term. Next, note that the divisor is x + 3 , x + 3 ,  which means that r =  − 3 . r =  − 3 .  The  − 3 − 3 is placed to the right. This gives us a top line of

coefficients → 120 − 43 − 4 − 3← r
coefficients → 120 − 43 − 4 − 3← r

Next, we carry the left coefficient, 1, to the bottom line and multiply it by r,  − 3 ,  − 3 ,  placing the product,  − 3 ,  − 3 ,  in the middle line under the second coefficient, 2. We then add the 2 and the  − 3 − 3 and place the result,  − 1 ,  − 1 ,  below. This gives

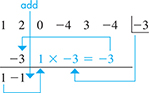
Synthetic division.

Now, multiply the  − 1 − 1 by  − 3( = r) − 3( = r) and place the result, 3, in the middle line under the zero. Now, add and continue the process, obtaining the following result:

The process depicts synthetic division of x to the fifth power + 2 to the fourth power minus 4 x squared + 3 x minus 4 by x + 3.

Because the degree of the dividend is 5, the degree of the quotient is 4. This means that the quotient is x4 − x3 + 3x2 − 13x + 42x4 − x3 + 3x2 − 13x + 42 and the remainder is  − 130 .  − 130 .  In turn, this means that for f(x) = x5 + 2x4 − 4x2 + 3x − 4 , f(x) = x5 + 2x4 − 4x2 + 3x − 4 ,  we have f( − 3) =  − 130 . f( − 3) =  − 130 . 

EXAMPLE 7 Using synthetic division

By synthetic division, divide 3x4 − 5x + 63x4 − 5x + 6 by x − 4 . x − 4 . 

300 − 561248192748312481877544
330121204848 − 519218767487544

The quotient is 3x3 + 12x2 + 48x + 187 , 3x3 + 12x2 + 48x + 187 ,  and the remainder is 754.

EXAMPLE 8 Checking factor with synthetic division

By synthetic division, determine whether or not t + 4t + 4 is a factor of t4 + 2t3 − 15t2 − 32t − 16 . t4 + 2t3 − 15t2 − 32t − 16 . 

12 − 15 − 32 − 16 − 4828161 − 2 − 7 − 40 − 4
112 − 4 − 2 − 158 − 7 − 3228 − 4 − 16160 − 4

Because the remainder is zero, t + 4t + 4 is a factor. We may also conclude that

f(t) = (t + 4)(t3 − 2t2 − 7t − 4)
f(t) = (t + 4)(t3 − 2t2 − 7t − 4)

EXAMPLE 9 Checking rational factor

By using synthetic division, determine whether 2x − 32x − 3 is a factor of 2x3 − 3x2 + 8x − 12 . 2x3 − 3x2 + 8x − 12 . 

CAUTION

We first note that the coefficient of x in the possible factor is not 1. Thus, we cannot use r = 3 , r = 3 ,  because the factor is not of the form x − r . x − r . 

However, 2x − 3 = 2(x − 32) , 2x − 3 = 2(x − 32) ,  which means that if 2(x − 32)2(x − 32) is a factor of the function, 2x − 32x − 3 is a factor. If we use r = 32r = 32 and find that the remainder is zero, then x − 32x − 32 is a factor.

2 − 38 − 123012208032
22 − 330808 − 1212032

Because the remainder is zero, x − 32x − 32 is a factor. Also, the quotient is 2x2 + 8 , 2x2 + 8 ,  which may be factored into 2(x2 + 4) . 2(x2 + 4) .  Thus, 2 is also a factor of the function. This means that 2(x − 32)2(x − 32) is a factor of the function, and this in turn means that 2x − 32x − 3 is a factor. This tells us that

2x3 − 3x2 + 8x − 12 = (2x − 3)(x2 + 4)
2x3 − 3x2 + 8x − 12 = (2x − 3)(x2 + 4)

EXAMPLE 10 Checking a zero

Determine whether or not  − 12.5 − 12.5 is a zero of the function f(x) = 6x3 + 61x2 − 171x + 100 . f(x) = 6x3 + 61x2 − 171x + 100 . 

If  − 12.5 − 12.5 is a zero of f(x), then x − ( − 12.5) , x − ( − 12.5) ,  or x + 12.5 , x + 12.5 ,  is a factor of f(x), and f( − 12.5) = 0 . f( − 12.5) = 0 .  We can find the remainder by direct use of the remainder theorem or by synthetic division.

Using synthetic division and a calculator to make the calculations, we have the following setup and calculator sequence:

661 − 171100 − 75175 − 506 − 14450 − 12.5
6661 − 75 − 14 − 1711754100 − 5050 − 12.5

Because the remainder is 50, and not zero,  − 12.5 − 12.5 is not a zero of f(x).

EXERCISES 15.1

In Exercises 1–4, make the given changes in the indicated examples of this section, and then perform the indicated operations.

  1. In Example 3, change the x + 4x + 4 to x + 3x + 3 and then find the remainder.

  2. In Example 4(a), change the t + 1t + 1 to t − 1t − 1 and then determine if t − 1t − 1 is a factor.

  3. In Example 6, change the x + 3x + 3 to x + 2x + 2 and then perform the synthetic division.

  4. In Example 9, change the 2x − 32x − 3 to 2x + 32x + 3 and then determine whether 2x + 32x + 3 is a factor.

In Exercises 5–10, find the remainder by long division.

  1. (x3 + 2x − 8) ÷ (x − 2)(x3 + 2x − 8) ÷ (x − 2)

  2. (x4 − 4x3 − x2 + x − 100) ÷ (x + 3)(x4 − 4x3 − x2 + x − 100) ÷ (x + 3)

  3. (2x5 − x2 + 8x + 44) ÷ (x + 1)(2x5 − x2 + 8x + 44) ÷ (x + 1)

  4. (4s3 − 9s2 − 24s − 17) ÷ (s − 5)(4s3 − 9s2 − 24s − 17) ÷ (s − 5)

  5. (2x4 − 3x3 − 2x2 − 15x − 16) ÷ (2x − 3)(2x4 − 3x3 − 2x2 − 15x − 16) ÷ (2x − 3)

  6. (2x4 − 11x2 − 15x − 17) ÷ (2x + 1)(2x4 − 11x2 − 15x − 17) ÷ (2x + 1)

In Exercises 11–16, find the remainder using the remainder theorem. Do not use synthetic division.

  1. (R4 + R3 − 9R2 + 3) ÷ (R − 3)(R4 + R3 − 9R2 + 3) ÷ (R − 3)

  2. (4x4 − x3 + 5x − 7) ÷ (x − 5)(4x4 − x3 + 5x − 7) ÷ (x − 5)

  3. (2x4 − 7x3 − x2 + 8) ÷ (x + 1)(2x4 − 7x3 − x2 + 8) ÷ (x + 1)

  4. (3n4 − 13n2 + 10n − 10) ÷ (n + 4)(3n4 − 13n2 + 10n − 10) ÷ (n + 4)

  5. (x5 − 3x3 + 5x2 − 10x + 6) ÷ (x + 2)(x5 − 3x3 + 5x2 − 10x + 6) ÷ (x + 2)

  6. (3x4 − 12x3 − 60x + 4) ÷ (x − 0.5)(3x4 − 12x3 − 60x + 4) ÷ (x − 0.5)

In Exercises 17–22, use the factor theorem to determine whether or not the second expression is a factor of the first expression. Do not use synthetic division.

  1. 8x3 + 2x2 − 32x − 8 ,  x − 28x3 + 2x2 − 32x − 8 ,  x − 2

  2. 3x3 + 14x2 + 7x − 4 ,  x + 43x3 + 14x2 + 7x − 4 ,  x + 4

  3. 3V4 − 7V3 + V + 8 ,  V − 23V4 − 7V3 + V + 8 ,  V − 2

  4. x5 − 2x4 + 3x3 − 6x2 − 4x + 8 ,  x − 1x5 − 2x4 + 3x3 − 6x2 − 4x + 8 ,  x − 1

  5. x51 − 2x − 1 ,  x + 1x51 − 2x − 1 ,  x + 1

  6. x7 − 128 − 1 ,  x + 2 − 1x7 − 128 − 1 ,  x + 2 − 1

In Exercises 23–32, perform the indicated divisions by synthetic division.

  1. (x3 + 2x2 − x − 2) ÷ (x − 1)(x3 + 2x2 − x − 2) ÷ (x − 1)

  2. (x3 − 3x2 − x + 2) ÷ (x − 3)(x3 − 3x2 − x + 2) ÷ (x − 3)

  3. (x3 + 2x2 − 3x + 4) ÷ (x + 4)(x3 + 2x2 − 3x + 4) ÷ (x + 4)

  4. (2x3 − 4x2 + x − 1) ÷ (x + 2)(2x3 − 4x2 + x − 1) ÷ (x + 2)

  5. (p6 − 6p3 − 2p2 − 6) ÷ (p − 2)(p6 − 6p3 − 2p2 − 6) ÷ (p − 2)

  6. (x5 + 4x4 − 8) ÷ (x + 1)(x5 + 4x4 − 8) ÷ (x + 1)

  7. (x7 − 128) ÷ (x − 2)(x7 − 128) ÷ (x − 2)

  8. (20x4 + 11x3 − 89x2 + 60x − 77) ÷ (x + 2.75)(20x4 + 11x3 − 89x2 + 60x − 77) ÷ (x + 2.75)

  9. (2x4 + x3 + 3x2 − 1) ÷ (2x − 1)(2x4 + x3 + 3x2 − 1) ÷ (2x − 1)

  10. (6t4 + 5t3 − 10t + 4) ÷ (3t − 2)(6t4 + 5t3 − 10t + 4) ÷ (3t − 2)

In Exercises 33–40, use the factor theorem and synthetic division to determine whether or not the second expression is a factor of the first.

  1. 2x5 − x3 + 3x2 − 4 ; x + 12x5 − x3 + 3x2 − 4 ; x + 1

  2. t5 − 3t4 − t2 − 6 ; t − 3t5 − 3t4 − t2 − 6 ; t − 3

  3. 4x3 − 9x2 + 2x − 2 ; x − 144x3 − 9x2 + 2x − 2 ; x − 14

  4. 3x3 − 5x2 + x + 1 ; x + 133x3 − 5x2 + x + 1 ; x + 13

  5. 2Z4 − Z3 − 4Z2 + 1 ; 2Z − 12Z4 − Z3 − 4Z2 + 1 ; 2Z − 1

  6. 6x4 + 5x3 − x2 + 6x − 2 ; 3x − 16x4 + 5x3 − x2 + 6x − 2 ; 3x − 1

  7. 4x4 + 2x3 − 8x2 + 3x + 12 ; 2x + 34x4 + 2x3 − 8x2 + 3x + 12 ; 2x + 3

  8. 3x4 − 2x3 + x2 + 15x + 4 ; 3x + 43x4 − 2x3 + x2 + 15x + 4 ; 3x + 4

In Exercises 41–44, use synthetic division to determine whether or not the given numbers are zeros of the given functions.

  1. x4 − 5x3 − 15x2 + 5x + 14 ; 7x4 − 5x3 − 15x2 + 5x + 14 ; 7

  2. r4 + 5r3 − 18r − 8 ;  − 4r4 + 5r3 − 18r − 8 ;  − 4

  3. 85x3 + 348x2 − 263x + 120 ;  − 4.885x3 + 348x2 − 263x + 120 ;  − 4.8

  4. 2x3 + 13x2 + 10x − 4 ; 122x3 + 13x2 + 10x − 4 ; 12

In Exercises 45–60, solve the given problems.

  1. If f(x) = 2x3 + 3x2 − 19x − 4 , f(x) = 2x3 + 3x2 − 19x − 4 ,  and f(x) = (x + 4)g(x) , f(x) = (x + 4)g(x) ,  find g (x).

  2. Using synthetic division, divide ax2 + bx + cax2 + bx + c by x + 1 . x + 1 . 

  3. By division, show that 2x − 12x − 1 is a factor of f(x) = 4x3 + 8x2 − x − 2 . f(x) = 4x3 + 8x2 − x − 2 .  May we therefore conclude that f(1) = 0 ? f(1) = 0 ?  Explain.

  4. By division, show that x2 + 2x2 + 2 is a factor of f(x) = 3x3 − x2 + 6x − 2 . f(x) = 3x3 − x2 + 6x − 2 .  May we therefore conclude that f( − 2) = 0 ? f( − 2) = 0 ?  Explain.

  5. For what value of k is x − 2x − 2 a factor of f(x) = 2x3 + kx2 − x + 14 ? f(x) = 2x3 + kx2 − x + 14 ? 

  6. For what value of k is x + 1x + 1 a factor of f(x) = 3x4 + 3x3 + 2x2 + kx − 4 ? f(x) = 3x4 + 3x3 + 2x2 + kx − 4 ? 

  7. Use synthetic division: (x3 − 3x2 + x − 3) ÷ (x + j) . (x3 − 3x2 + x − 3) ÷ (x + j) . 

  8. Use synthetic division: (2x3 − 7x2 + 10x − 6) ÷ [ x − (1 + j)]  . (2x3 − 7x2 + 10x − 6) ÷ [ x − (1 + j)]  . 

  9. If f(x) =  − g(x) , f(x) =  − g(x) ,  do the functions have the same zeros? Explain.

  10. Do the functions f(x) and f( − x)f( − x) have the same zeros? Explain.

  11. If f(x) = 3x3 − 5ax2 − 3a2x + 5a3 , f(x) = 3x3 − 5ax2 − 3a2x + 5a3 ,  find f(x) ÷ (x + a) . f(x) ÷ (x + a) . 

  12. The length of a rectangular box is 3 cm longer than its width. If the volume as a function of the width is f(w) = 2w3 + 5w2 − 3w , f(w) = 2w3 + 5w2 − 3w ,  find the height if the box.

  13. In finding the electric current in a certain circuit, it is necessary to factor the denominator of 2ss3 + 5s2 + 4s + 20 . 2ss3 + 5s2 + 4s + 20 .  Is (a) (s − 2)(s − 2) or (b) (s + 5)(s + 5) a factor?

  14. In the theory of the motion of a sphere moving through a fluid, the function f(r) = 4r3 − 3ar2 − a3f(r) = 4r3 − 3ar2 − a3 is used. Is (a) r = ar = a or (b) r = 2ar = 2a a zero of f(r)?

  15. In finding the volume V (in cm3cm3) of a certain gas in equilibrium with a liquid, it is necessary to solve the equation V3 − 6V2 + 12V = 8 . V3 − 6V2 + 12V = 8 .  Use synthetic division to determine if V = 2 cm3 . V = 2 cm3 . 

  16. An architect is designing a window in the shape of a segment of a circle. An approximate formula for the area is A = h32w + 2wh3 , A = h32w + 2wh3 ,  where A is the area, w is the width, and h is the height of the segment. If the width is 1.500 m and the area is 0.5417 m2 , 0.5417 m2 ,  use synthetic division to show that h = 0.500 m . h = 0.500 m . 

Answers to Practice Exercises

  1. No (R = 2)(R = 2)

  2. Yes (R = 0)(R = 0)

  3. Quotient: 3x2 − 6x + 7 ,  R =  − 83x2 − 6x + 7 ,  R =  − 8

  4. No (R = 4)(R = 4)

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.21.76.0