Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1.2 Fundamental Operations of Algebra

Fundamental Laws of Algebra • Operations on Positive and Negative Numbers • Order of Operations • Operations with Zero

If two numbers are added, it does not matter in which order they are added. (For example, $5 + 3 = 8$ $5 + 3 = 8$ and $3 + 5 = 8,$ $3 + 5 = 8,$ or $5 + 3 = 3 + 5.$ $5 + 3 = 3 + 5.$ ) This statement, generalized and accepted as being correct for all possible combinations of numbers being added, is called the commutative law for addition. It states that the sum of two numbers is the same, regardless of the order in which they are added. We make no attempt to prove this law in general, but accept that it is true.

In the same way, we have the associative law for addition, which states that the sum of three or more numbers is the same, regardless of the way in which they are grouped for addition. For example, $3 + (5 + 6) = (3 + 5) + 6.$ $3 + (5 + 6) = (3 + 5) + 6.$

The laws just stated for addition are also true for multiplication. Therefore, the product of two numbers is the same, regardless of the order in which they are multiplied, and the product of three or more numbers is the same, regardless of the way in which they are grouped for multiplication. For example, $2 \times 5 = 5 \times 2,$ $2 \times 5 = 5 \times 2,$ and $5 \times (4 \times 2) = (5 \times 4) \times 2.$ $5 \times (4 \times 2) = (5 \times 4) \times 2.$

Another very important law is the distributive law. It states that the product of one number and the sum of two or more other numbers is equal to the sum of the products of the first number and each of the other numbers of the sum. For example,

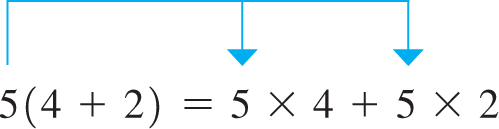
An equation represents fundamental operations, 5 times left parenthesis 4 plus 2 right parenthesis equals 5 times 4, plus 5 times 2.

In this case, it can be seen that the total is 30 on each side.

In practice, we use these fundamental laws of algebra naturally without thinking about them, except perhaps for the distributive law.

Not all operations are commutative and associative. For example, division is not commutative, because the order of division of two numbers does matter. For instance, $\frac{6}{5} \neq \frac{5}{6}$ $\frac{6}{5} \neq \frac{5}{6}$ $(\neq$ $(\neq$ is read “does not equal”). (Also, see Exercise 54.)

Using literal numbers, the fundamental laws of algebra are as follows:

Commutative law of addition: $a + b = b + a$ $a + b = b + a$
Associative law of addition: $a + (b + c) = (a + b) + c$ $a + (b + c) = (a + b) + c$
Commutative law of multiplication: $a b = b a$ $a b = b a$
Associative law of multiplication: $a (b c) = (a b) c$ $a (b c) = (a b) c$
Distributive law: $a (b + c) = a b + a c$ $a (b + c) = a b + a c$

Each of these laws is an example of an identity, in that the expression to the left of the $=$ $=$ sign equals the expression to the right for any value of each of a, b, and c.

OPERATIONS ON POSITIVE AND NEGATIVE NUMBERS

When using the basic operations (addition, subtraction, multiplication, division) on positive and negative numbers, we determine the result to be either positive or negative according to the following rules.

Addition of two numbers of the same sign Add their absolute values and assign the sum their common sign.

EXAMPLE 1 Adding numbers of the same sign

$2 + 6 = 8 the sum of two positive numbers is positive$ $2 + 6 = 8 the sum of two positive numbers is positive$
$- 2 + (- 6) = - (2 + 6) = - 8 the sum of two negative numbers is negative$ $- 2 + (- 6) = - (2 + 6) = - 8 the sum of two negative numbers is negative$

The negative number $- 6$ $- 6$ is placed in parentheses because it is also preceded by a plus sign showing addition. It is not necessary to place the $- 2$ $- 2$ in parentheses.

Addition of two numbers of different signs Subtract the number of smaller absolute value from the number of larger absolute value and assign to the result the sign of the number of larger absolute value.

EXAMPLE 2 Adding numbers of different signs

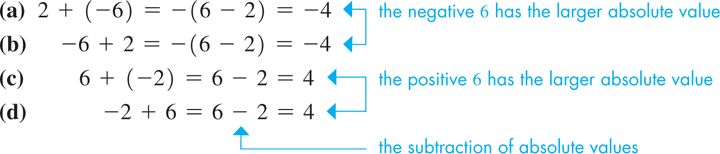
A mathematical operation for adding numbers of different signs is carried out in four steps.

.2-2 Full Alternative Text

Subtraction of one number from another Change the sign of the number being subtracted and change the subtraction to addition. Perform the addition.

EXAMPLE 3 Subtracting positive and negative numbers

$2 - 6 = 2 + (- 6) = - (6 - 2) = - 4$ $2 - 6 = 2 + (- 6) = - (6 - 2) = - 4$

Note that after changing the subtraction to addition, and changing the sign of 6 to make it $- 6,$ $- 6,$ we have precisely the same illustration as Example 2(a).
$- 2 - 6 = - 2 + (- 6) = - (2 + 6) = - 8$ $- 2 - 6 = - 2 + (- 6) = - (2 + 6) = - 8$

Note that after changing the subtraction to addition, and changing the sign of 6 to make it $- 6,$ $- 6,$ we have precisely the same illustration as Example 1(b).
$- a - (- a) = - a + a = 0$ $- a - (- a) = - a + a = 0$

This shows that subtracting a number from itself results in zero, even if the number is negative.

NOTE

[Subtracting a negative number is equivalent to adding a positive number of the same absolute value.]
$- 2 - (- 6) = - 2 + 6 = 4$ $- 2 - (- 6) = - 2 + 6 = 4$
The change in temperature from $- 12 ° C$ $- 12 ° C$ to $- 26 ° C$ $- 26 ° C$ is $- 26 ° C - (- 12 ° C) = - 26 ° C + 12 ° C = - 14 ° C$ $- 26 ° C - (- 12 ° C) = - 26 ° C + 12 ° C = - 14 ° C$

Multiplication and division of two numbers The product (or quotient) of two numbers of the same sign is positive. The product (or quotient) of two numbers of different signs is negative.

EXAMPLE 4 Multiplying and dividing positive and negative numbers

\begin{array}{lrclrcll} (a) & 3 (12) & = & 3 \times 12 = 36 & \frac{12}{3} & = & 4 & \begin{array}{l} result is positive if both \\ numbers are positive \end{array} \\ (b) & - 3 (- 12) & = & 3 \times 12 = 36 & \frac{- 12}{- 3} & = & 4 & \begin{array}{l} result is positive if both \\ numbers are negative \end{array} \\ (c) & 3 (- 12) & = & - (3 \times 12) = - 36 & \frac{- 12}{3} & = & - \frac{12}{3} = - 4 & \begin{array}{l} result is negative if one \\ number is positive and \\ the other is negative \end{array} \\ (d) & - 3 (12) & = & - (3 \times 12) = - 36 & \frac{12}{- 3} & = & - \frac{12}{3} = - 4 \end{array}

$\begin{array}{lrclrcll} (a) & 3 (12) & = & 3 \times 12 = 36 & \frac{12}{3} & = & 4 & \begin{array}{l} result is positive if both \\ numbers are positive \end{array} \\ (b) & - 3 (- 12) & = & 3 \times 12 = 36 & \frac{- 12}{- 3} & = & 4 & \begin{array}{l} result is positive if both \\ numbers are negative \end{array} \\ (c) & 3 (- 12) & = & - (3 \times 12) = - 36 & \frac{- 12}{3} & = & - \frac{12}{3} = - 4 & \begin{array}{l} result is negative if one \\ number is positive and \\ the other is negative \end{array} \\ (d) & - 3 (12) & = & - (3 \times 12) = - 36 & \frac{12}{- 3} & = & - \frac{12}{3} = - 4 \end{array}$

ORDER OF OPERATIONS

Often, how we are to combine numbers is clear by grouping the numbers using symbols such as parentheses, ( ); the bar, , between the numerator and denominator of a fraction; and vertical lines for absolute value. Otherwise, for an expression in which there are several operations, we use the following order of operations.

EXAMPLE 5 Order of operations

$20 \div (2 + 3)$ $20 \div (2 + 3)$ is evaluated by first adding $2 + 3$ $2 + 3$ and then dividing. The grouping of $2 + 3$ $2 + 3$ is clearly shown by the parentheses. Therefore, $20 \div (2 + 3) = 20 \div 5 = 4.$ $20 \div (2 + 3) = 20 \div 5 = 4.$
$20 \div 2 + 3$ $20 \div 2 + 3$ is evaluated by first dividing 20 by 2 and then adding. No specific grouping is shown, and therefore the division is done before the addition. This means $20 \div 2 + 3 = 10 + 3 = 13.$ $20 \div 2 + 3 = 10 + 3 = 13.$
Therefore, $16 - 2 \times 3 = 16 - 6 = 10.$ $16 - 2 \times 3 = 16 - 6 = 10.$

NOTE

[ $16 - 2 \times 3$ $16 - 2 \times 3$ is evaluated by first multiplying 2 by 3 and then subtracting. We do not first subtract 2 from 16.]
$16 \div 2 \times 4$ $16 \div 2 \times 4$ is evaluated by first dividing 16 by 2 and then multiplying. From left to right, the division occurs first. Therefore, $16 \div 2 \times 4 = 8 \times 4 = 32.$ $16 \div 2 \times 4 = 8 \times 4 = 32.$
$| 3 - 5 | - | - 3 - 6 |$ $| 3 - 5 | - | - 3 - 6 |$ is evaluated by first performing the subtractions within the absolute value vertical bars, then evaluating the absolute values, and then subtracting. This means that $| 3 - 5 | - | - 3 - 6 | = | - 2 | - | - 9 | = 2 - 9 = - 7.$ $| 3 - 5 | - | - 3 - 6 | = | - 2 | - | - 9 | = 2 - 9 = - 7.$

When evaluating expressions, it is generally more convenient to change the operations and numbers so that the result is found by the addition and subtraction of positive numbers. When this is done, we must remember that

a + (- b) = a - b

$a + (- b) = a - b$ (1.1)

a - (- b) = a + b

$a - (- b) = a + b$ (1.2)

EXAMPLE 6 Evaluating numerical expressions

$7 + (- 3) - 6 = 7 - 3 - 6 = 4 - 6 = - 2$ $7 + (- 3) - 6 = 7 - 3 - 6 = 4 - 6 = - 2$ using Eq. (1.1)
$\frac{18}{- 6} + 5 - (- 2) (3) = - 3 + 5 - (- 6) = 2 + 6 = 8$ $\frac{18}{- 6} + 5 - (- 2) (3) = - 3 + 5 - (- 6) = 2 + 6 = 8$ using Eq. (1.2)
$\frac{| 3 - 15 |}{- 2} - \frac{8}{4 - 6} = \frac{12}{- 2} - \frac{8}{- 2} = - 6 - (- 4) = - 6 + 4 = - 2$ $\frac{| 3 - 15 |}{- 2} - \frac{8}{4 - 6} = \frac{12}{- 2} - \frac{8}{- 2} = - 6 - (- 4) = - 6 + 4 = - 2$
$\frac{- 12}{2 - 8} + \frac{5 - 1}{2 (- 1)} = \frac{- 12}{- 6} + \frac{4}{- 2} = 2 + (- 2) = 2 - 2 = 0$ $\frac{- 12}{2 - 8} + \frac{5 - 1}{2 (- 1)} = \frac{- 12}{- 6} + \frac{4}{- 2} = 2 + (- 2) = 2 - 2 = 0$

In illustration (b), we see that the division and multiplication were done before the addition and subtraction. In (c) and (d), we see that the groupings were evaluated first. Then we did the divisions, and finally the subtraction and addition.

EXAMPLE 7 Evaluating—velocity after collision

A 3000-lb van going at 40 mi/h ran head-on into a 2000-lb car going at 20 mi/h. An insurance investigator determined the velocity of the vehicles immediately after the collision from the following calculation. See Fig. 1.5.

A diagram of a 3,000 pound van going 40 miles per hour hitting a 2,000 pound car going 20 miles per hour. — Fig. 1.5

Figure 1.5 Full Alternative Text

\begin{array}{rcl} \frac{3000 (40) + (2000) (- 20)}{3000 + 2000} & = & \frac{120, 000 + (- 40, 000)}{3000 + 2000} = \frac{120, 000 - 40, 000}{5000} \\ = & \frac{80, 000}{5000} = 16 mi / h \end{array}

$\begin{array}{rcl} \frac{3000 (40) + (2000) (- 20)}{3000 + 2000} & = & \frac{120, 000 + (- 40, 000)}{3000 + 2000} = \frac{120, 000 - 40, 000}{5000} \\ = & \frac{80, 000}{5000} = 16 mi / h \end{array}$

The numerator and the denominator must be evaluated before the division is performed. The multiplications in the numerator are performed first, followed by the addition in the denominator and the subtraction in the numerator.

OPERATIONS WITH ZERO

Because operations with zero tend to cause some difficulty, we will show them here.

If a is a real number, the operations of addition, subtraction, multiplication, and division with zero are as follows:

\begin{array}{rcl} a + 0 & = & a \\ a - 0 & = & a 0 - a = - a \\ a \times 0 & = & 0 \\ 0 \div a & = & \frac{0}{a} = 0 (if a \neq 0) \neq means “ is not equal to ” \end{array}

$\begin{array}{rcl} a + 0 & = & a \\ a - 0 & = & a 0 - a = - a \\ a \times 0 & = & 0 \\ 0 \div a & = & \frac{0}{a} = 0 (if a \neq 0) \neq means “ is not equal to ” \end{array}$

EXAMPLE 8 Operations with zero

$5 + 0 = 5$ $5 + 0 = 5$
$- 6 - 0 = - 6$ $- 6 - 0 = - 6$
$0 - 4 = - 4$ $0 - 4 = - 4$
$\frac{0}{6} = 0$ $\frac{0}{6} = 0$
$\frac{0}{- 3} = 0$ $\frac{0}{- 3} = 0$
$\frac{5 \times 0}{7} = \frac{0}{7} = 0$ $\frac{5 \times 0}{7} = \frac{0}{7} = 0$

Note that there is no result defined for division by zero. To understand the reason for this, consider the results for $\frac{6}{2}$ $\frac{6}{2}$ and $\frac{6}{0} .$ $\frac{6}{0} .$

\frac{6}{2} = 3 since 2 \times 3 = 6

$\frac{6}{2} = 3 since 2 \times 3 = 6$

If $\frac{6}{0} = b,$ $\frac{6}{0} = b,$ then $0 \times b = 6.$ $0 \times b = 6.$ This cannot be true because $0 \times b = 0$ $0 \times b = 0$ for any value of b. Thus, division by zero is undefined.

(The special case of $\frac{0}{0}$ $\frac{0}{0}$ is termed indeterminate. If $\frac{0}{0} = b,$ $\frac{0}{0} = b,$ then $0 = 0 \times b,$ $0 = 0 \times b,$ which is true for any value of b. Therefore, no specific value of b can be determined.)

EXAMPLE 9 Division by zero is undefined

Mathematical equations involving division by zero. 2 fifths divided by 0 is undefined. 8 over 0 is undefined. 7 times 0 over 0 times 6 is indeterminate.

see above

CAUTION

The operations with zero will not cause any difficulty if we remember to never divide by zero.

Division by zero is the only undefined basic operation. All the other operations with zero may be performed as for any other number.

EXERCISES 1.2

In Exercises 1–4, make the given changes in the indicated examples of this section, and then solve the resulting problems.

In Example 5(c), change 3 to $(- 2)$ $(- 2)$ and then evaluate.
In Example 6(b), change 18 to $- 18$ $- 18$ and then evaluate.
In Example 6(d), interchange the 2 and 8 in the first denominator and then evaluate.
In the rightmost illustration in Example 9, interchange the 6 and the 0 above the 6. Is any other change needed?

In Exercises 5–38, evaluate each of the given expressions by performing the indicated operations.

$5 + (- 8)$ $5 + (- 8)$
$- 4 + (- 7)$ $- 4 + (- 7)$
$- 3 + 9$ $- 3 + 9$
$18 - 21$ $18 - 21$
$- 19 - (- 16)$ $- 19 - (- 16)$
$- 8 - (- 10)$ $- 8 - (- 10)$
$7 (- 4)$ $7 (- 4)$
$- 9 (3)$ $- 9 (3)$
$- 7 (- 5)$ $- 7 (- 5)$
$\frac{- 9}{3}$ $\frac{- 9}{3}$
$\frac{- 6 (20 - 10)}{- 3}$ $\frac{- 6 (20 - 10)}{- 3}$
$\frac{- 28}{- 7 (5 - 6)}$ $\frac{- 28}{- 7 (5 - 6)}$
$- 2 (4) (- 5)$ $- 2 (4) (- 5)$
$- 3 (- 4) (- 6)$ $- 3 (- 4) (- 6)$
$2 (2 - 7) \div 10$ $2 (2 - 7) \div 10$
$\frac{- 64}{- 2 | 4 - 8 |}$ $\frac{- 64}{- 2 | 4 - 8 |}$
$16 \div 2 (- 4)$ $16 \div 2 (- 4)$
$- 20 \div 5 (- 4)$ $- 20 \div 5 (- 4)$
$- 9 - | 2 - 10 |$ $- 9 - | 2 - 10 |$
$(7 - 7) \div (5 - 7)$ $(7 - 7) \div (5 - 7)$
$\frac{17 - 7}{7 - 7}$ $\frac{17 - 7}{7 - 7}$
$\frac{(7 - 7) (2)}{(7 - 7) (- 1)}$ $\frac{(7 - 7) (2)}{(7 - 7) (- 1)}$
$8 - 3 (- 4)$ $8 - 3 (- 4)$
$- 20 + 8 \div 4$ $- 20 + 8 \div 4$
$- 2 (- 6) + | \frac{8}{- 2} |$ $- 2 (- 6) + | \frac{8}{- 2} |$
$\frac{| - 2 |}{- 2} - (- 2) (- 5)$ $\frac{| - 2 |}{- 2} - (- 2) (- 5)$
$10 (- 8) (- 3) \div (10 - 50)$ $10 (- 8) (- 3) \div (10 - 50)$
$\frac{7 - | - 5 |}{- 1 (- 2)}$ $\frac{7 - | - 5 |}{- 1 (- 2)}$
$\frac{24}{3 + (- 5)} - 4 (- 9) \div (- 3)$ $\frac{24}{3 + (- 5)} - 4 (- 9) \div (- 3)$
$\frac{- 18}{3} - \frac{4 - | - 6 |}{- 1}$ $\frac{- 18}{3} - \frac{4 - | - 6 |}{- 1}$
$- 7 - \frac{| - 14 |}{2 (2 - 3)} - 3 | 6 - 8 |$ $- 7 - \frac{| - 14 |}{2 (2 - 3)} - 3 | 6 - 8 |$
$- 7 (- 3) + \frac{- 6}{- 3} - | - 9 |$ $- 7 (- 3) + \frac{- 6}{- 3} - | - 9 |$
$\frac{3 | - 9 - 2 (- 3) |}{1 + (- 10)}$ $\frac{3 | - 9 - 2 (- 3) |}{1 + (- 10)}$
$\frac{20 (- 12) - 40 (- 15)}{98 - | - 98 |}$ $\frac{20 (- 12) - 40 (- 15)}{98 - | - 98 |}$

In Exercises 39–46, determine which of the fundamental laws of algebra is demonstrated.

$6 (7) = 7 (6)$ $6 (7) = 7 (6)$
$6 + 8 = 8 + 6$ $6 + 8 = 8 + 6$
$6 (3 + 1) = 6 (3) + 6 (1)$ $6 (3 + 1) = 6 (3) + 6 (1)$
$4 (5 \times π) = (4 \times 5) (π)$ $4 (5 \times π) = (4 \times 5) (π)$
$3 + (5 + 9) = (3 + 5) + 9$ $3 + (5 + 9) = (3 + 5) + 9$
$8 (3 - 2) = 8 (3) - 8 (2)$ $8 (3 - 2) = 8 (3) - 8 (2)$
$(\sqrt{5} \times 3) \times 9 = \sqrt{5} \times (3 \times 9)$ $(\sqrt{5} \times 3) \times 9 = \sqrt{5} \times (3 \times 9)$
$(3 \times 6) \times 7 = 7 \times (3 \times 6)$ $(3 \times 6) \times 7 = 7 \times (3 \times 6)$

In Exercises 47–50, for numbers a and b, determine which of the following expressions equals the given expression.

$a + b$ $a + b$
$a - b$ $a - b$
$b - a$ $b - a$
$- a - b$ $- a - b$

$- a + (- b)$ $- a + (- b)$
$b - (- a)$ $b - (- a)$
$- b - (- a)$ $- b - (- a)$
$- a - (- b)$ $- a - (- b)$

In Exercises 51–66, solve the given problems. Refer to Appendix B for units of measurement and their symbols.

Insert the proper sign $(=, >, <)$ $(=, >, <)$ to make the following true: $| 5 - (- 2) | | - 5 - | - 2 | |$ $| 5 - (- 2) | | - 5 - | - 2 | |$
Insert the proper sign $(=, >, <)$ $(=, >, <)$ to make the following true: $| - 3 - | - 7 | | | | - 3 | - 7 |$ $| - 3 - | - 7 | | | | - 3 | - 7 |$
(a) What is the sign of the product of an even number of negative numbers? (b) What is the sign of the product of an odd number of negative numbers?
Is subtraction commutative? Explain.
Explain why the following definition of the absolute value of a real number x is either correct or incorrect (the symbol $\geq$ $\geq$ means “is equal to or greater than”): If $x \geq 0,$ $x \geq 0,$ then $| x | = x;$ $| x | = x;$ if $x < 0,$ $x < 0,$ then $| x | = - x$ $| x | = - x$ .
Explain what is the error if the expression $24 - 6 \div 2 \cdot 3$ $24 - 6 \div 2 \cdot 3$ is evaluated as 27. What is the correct value?
Describe the values of x and y for which (a) $- x y = 1$ $- x y = 1$ and (b) $\frac{x - y}{x - y} = 1.$ $\frac{x - y}{x - y} = 1.$
Describe the values of x and y for which (a) $| x + y | = | x | + | y |$ $| x + y | = | x | + | y |$ and (b) $| x - y | = | x | + | y | .$ $| x - y | = | x | + | y | .$
The changes in the price of a stock (in dollars) for a given week were $- 0.68, + 0.42, + 0.06, - 0.11,$ $- 0.68, + 0.42, + 0.06, - 0.11,$ and $+ 0.02.$ $+ 0.02.$ What was the total change in the stock’s price that week?
Using subtraction of signed numbers, find the difference in the altitude of the bottom of the Dead Sea, 1396 m below sea level, and the bottom of Death Valley, 86 m below sea level.
Some solar energy systems are used to supplement the utility company power supplied to a home such that the meter runs backward if the solar energy being generated is greater than the energy being used. With such a system, if the solar power averages 1.5 kW for a 3.0-h period and only $2.1 kW \cdot h$ $2.1 kW \cdot h$ is used during this period, what will be the change in the meter reading for this period? Hint: Solar power generated makes the meter run in the negative direction while power used makes it run in the positive direction.
A baseball player’s batting average (total number of hits divided by total number of at-bats) is expressed in decimal form from 0.000 (no hits for all at-bats) to 1.000 (one hit for each at-bat). A player’s batting average is often shown as 0.000 before the first at-bat of the season. Is this a correct batting average? Explain.
The daily high temperatures (in $° C$ $° C$ ) for Edmonton, Alberta, in the first week in March were recorded as $- 7, - 3,$ $- 7, - 3,$ 2, 3, 1, $- 4,$ $- 4,$ and $- 6.$ $- 6.$ What was the average daily temperature for the week? (Divide the algebraic sum of readings by the number of readings.)
A flare is shot up from the top of a tower. Distances above the flare gun are positive and those below it are negative. After 5 s the vertical distance (in ft) of the flare from the flare gun is found by evaluating $(70) (5) + (- 16) (25) .$ $(70) (5) + (- 16) (25) .$ Find this distance.
Find the sum of the voltages of the batteries shown in Fig. 1.6. Note the directions in which they are connected.

Fig. 1.6

Figure 1.6 Full Alternative Text
A faulty gauge on a fire engine pump caused the apparent pressure in the hose to change every few seconds. The pressures (in $lb / {in.}^{2}$ $lb / {in.}^{2}$ above and below the set pressure were recorded as: $+ 7, - 2, - 9, - 6.$ $+ 7, - 2, - 9, - 6.$ What was the change between (a) the first two readings, (b) between the middle two readings, and (c) the last two readings?
One oil-well drilling rig drills 100 m deep the first day and 200 m deeper the second day. A second rig drills 200 m deep the first day and 100 m deeper the second day. In showing that the total depth drilled by each rig was the same, state what fundamental law of algebra is illustrated.
A water tank leaks 12 gal each hour for 7 h, and a second tank leaks 7 gal each hour for 12 h. In showing that the total amount leaked is the same for the two tanks, what fundamental law of algebra is illustrated?
On each of the 7 days of the week, a person spends 25 min on Facebook and 15 min on Twitter. Set up the expression for the total time spent on these two sites that week. What fundamental law of algebra is illustrated?
A jet travels 600 mi/h relative to the air. The wind is blowing at 50 mi/h. If the jet travels with the wind for 3 h, set up the expression for the distance traveled. What fundamental law of algebra is illustrated?

Answers to Practice Exercises

3
40
9
2
$- 4$ $- 4$
8

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 1.2 Fundamental Operations of Algebra

Create new playlist

Sign In

Sign Up

Table of Contents for
1.2 Fundamental Operations of Algebra