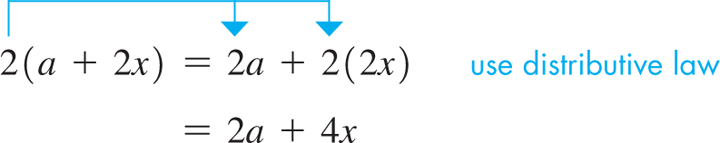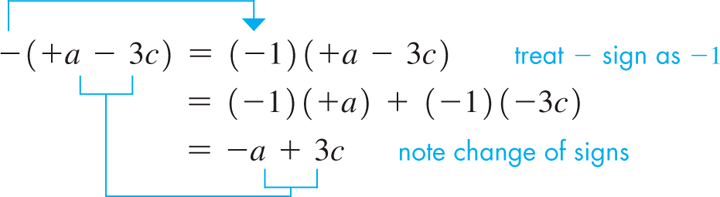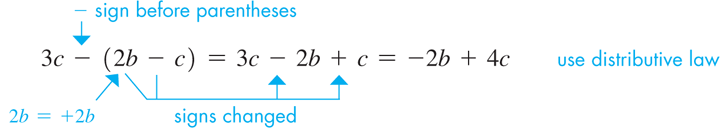Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1.7 Addition and Subtraction of Algebraic Expressions

Algebraic Expressions • Terms • Factors • Polynomials • Similar Terms • Simplifying • Symbols of Grouping

Because we use letters to represent numbers, we can see that all operations that can be used on numbers can also be used on literal numbers. In this section, we discuss the methods for adding and subtracting literal numbers.

Addition, subtraction, multiplication, division, and taking powers or roots are known as algebraic operations. Any combination of numbers and literal symbols that results from algebraic operations is known as an algebraic expression.

When an algebraic expression consists of several parts connected by plus signs and minus signs, each part (along with its sign) is known as a term of the expression. If a given expression is made up of the product of a number of quantities, each of these quantities, or any product of them, is called a factor of the expression.

CAUTION

It is very important to distinguish clearly between terms and factors, because some operations that are valid for terms are not valid for factors, and conversely. Some of the common errors in handling algebraic expressions occur because these operations are not handled properly.

EXAMPLE 1 Terms and factors

In the study of the motion of a rocket, the following algebraic expression may be used.

An equation with its terms and factors explained. The equation has 3 terms. the first term, g t squared has a factor of, g and 2 factors of, t. The second term, negative 2 v t has 3 factors, 2, v and t. The third term 2 s has 2 factors, 2 and s.

This expression has three terms: $g t^{2}, - 2 v t,$ $g t^{2}, - 2 v t,$ and 2s. The first term, $g t^{2},$ $g t^{2},$ has a factor of g and two factors of t. Any product of these factors is also a factor of $g t^{2} .$ $g t^{2} .$ This means other factors are gt, $t^{2},$ $t^{2},$ and $g t^{2}$ $g t^{2}$ itself.

EXAMPLE 2 Terms and factors

$7 a (x^{2} + 2 y) - 6 x (5 + x - 3 y)$ $7 a (x^{2} + 2 y) - 6 x (5 + x - 3 y)$ is an expression with terms $7 a (x^{2} + 2 y)$ $7 a (x^{2} + 2 y)$ and $- 6 x (5 + x - 3 y) .$ $- 6 x (5 + x - 3 y) .$

The term $7 a (x^{2} + 2 y)$ $7 a (x^{2} + 2 y)$ has individual factors of 7, a, and $(x^{2} + 2 y),$ $(x^{2} + 2 y),$ as well as products of these factors. The factor $x^{2} + 2 y$ $x^{2} + 2 y$ has two terms, $x^{2}$ $x^{2}$ and 2y.

The term $- 6 x (5 + x - 3 y)$ $- 6 x (5 + x - 3 y)$ has factors 2, 3, x, and $(5 + x - 3 y) .$ $(5 + x - 3 y) .$ The negative sign in front can be treated as a factor of $- 1.$ $- 1.$ The factor $5 + x - 3 y$ $5 + x - 3 y$ has three terms, 5, x, and $- 3 y .$ $- 3 y .$

A polynomial is an algebraic expression with only nonnegative integer exponents on one or more variables, and has no variable in a denominator. The degree of a term is the sum of the exponents of the variables of that term, and the degree of the polynomial is the degree of the term of highest degree.

A multinomial is any algebraic expression of more than one term. Terms like 1/x and $\sqrt{x}$ $\sqrt{x}$ can be included in a multinomial, but not in a polynomial. (Since $1 / x = x^{- 1},$ $1 / x = x^{- 1},$ the exponent is negative.)

EXAMPLE 3 Polynomials

Some examples of polynomials are as follows:

$4 x^{2} - 5 x + 3$ $4 x^{2} - 5 x + 3$ (degree 2)
$2 x^{6} - x$ $2 x^{6} - x$ (degree 6)
3x (degree 1)
$x y^{3} + 7 x - 3$ $x y^{3} + 7 x - 3$ (degree 4) (add exponents of x and y)
$- 6$ $- 6$ (degree 0) $(- 6 = - 6 x^{0})$ $(- 6 = - 6 x^{0})$

From (c), note that a single term can be a polynomial, and from (e), note that a constant can be a polynomial. The expressions in (a), (b), and (d) are also multinomials.

The expression $x^{2} + \sqrt{y + 2} - 8$ $x^{2} + \sqrt{y + 2} - 8$ is a multinomial, but not a polynomial because of the square root term.

A polynomial with one term is called a monomial. A polynomial with two terms is called a binomial, and one with three terms is called a trinomial. The numerical factor is called the numerical coefficient (or simply coefficient) of the term. All terms that differ at most in their numerical coefficients are known as similar or like terms. That is, similar terms have the same variables with the same exponents.

EXAMPLE 4 Monomial, binomial, trinomial

$7 x^{4}$ $7 x^{4}$ is a monomial. The numerical coefficient is 7.
$3 a b - 6 a$ $3 a b - 6 a$ is a binomial. The numerical coefficient of the first term is 3, and the numerical coefficient of the second term is $- 6.$ $- 6.$ Note that the sign is attached to the coefficient.
$8 c x^{3} - x + 2$ $8 c x^{3} - x + 2$ is a trinomial. The coefficients of the first two terms are 8 and $- 1.$ $- 1.$
$x^{2} y^{2} - 2 x + 3 y - 9$ $x^{2} y^{2} - 2 x + 3 y - 9$ is a polynomial with four terms (no special name).

EXAMPLE 5 Similar terms

$8 b - 6 a b + 81 b$ $8 b - 6 a b + 81 b$ is a trinomial. The first and third terms are similar because they differ only in their numerical coefficients. The middle term is not similar to the others because it has a factor of a.
$4 x^{2} - 3 x$ $4 x^{2} - 3 x$ is a binomial. The terms are not similar since the first term has two factors of x, and the second term has only one factor of x.
$3 x^{2} y^{3} - 5 y^{3} x^{2} + x^{2} - 2 y^{3}$ $3 x^{2} y^{3} - 5 y^{3} x^{2} + x^{2} - 2 y^{3}$ is a polynomial. The commutative law tells us that $x^{2} y^{3} = y^{3} x^{2},$ $x^{2} y^{3} = y^{3} x^{2},$ which means the first two terms are similar.

In adding and subtracting algebraic expressions, we combine similar terms into a single term. The simplified expression will contain only terms that are not similar.

EXAMPLE 6 Simplifying expressions

$6 a^{2} - 7 a + 8 a x$ $6 a^{2} - 7 a + 8 a x$ cannot be simplified since there are no like terms.

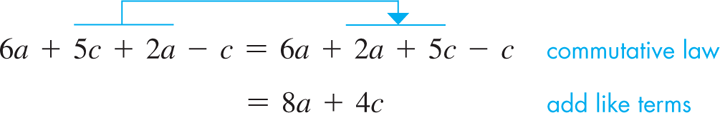
To group terms in an algebraic expression, we use symbols of grouping. In this text, we use parentheses, ( ); brackets, [ ]; and braces, ${} .$ ${} .$ All operations that occur in the numerator or denominator of a fraction are implied to be inside grouping symbols, as well as all operations under a radical symbol.

CAUTION

In simplifying an expression using the distributive law, to remove the symbols of grouping if a MINUS sign precedes the grouping, change the sign of EVERY term in the grouping, or if a plus sign precedes the grouping retain the sign of every term.

EXAMPLE 7 Symbols of grouping

.7-6 Full Alternative Text

Normally, $+ a$ $+ a$ would be written simply as a.

EXAMPLE 8 Simplifying: signs before parentheses

.7-6 Full Alternative Text
.7-6 Full Alternative Text
.7-6 Full Alternative Text
$\begin{array}{rcl} y (3 - y) - 2 (y - 3) & = & 3 y - y^{2} - 2 y + 6 note the - 2 (- 3) = + 6 \\ = & - y^{2} + y + 6 \end{array}$ $\begin{array}{rcl} y (3 - y) - 2 (y - 3) & = & 3 y - y^{2} - 2 y + 6 note the - 2 (- 3) = + 6 \\ = & - y^{2} + y + 6 \end{array}$

EXAMPLE 9 Simplifying—machine part design

In designing a certain machine part, it is necessary to perform the following simplification.

An equation illustrates the process of simplification an expression in 3 steps.

.7-6 Full Alternative Text

At times, we have expressions in which more than one symbol of grouping is to be removed in the simplification.

NOTE

[Normally, when several symbols of grouping are to be removed, it is more convenient to remove the innermost symbols first.]

CAUTION

One of the most common errors made is changing the sign of only the first term when removing symbols of grouping preceded by a minus sign. Remember, if the symbols are preceded by a minus sign, we must change the sign of every term.

EXAMPLE 10 Several symbols of grouping

Calculators use only parentheses for grouping symbols, and we often need to use one set of parentheses within another set. These are called nested parentheses. In the next example, note that the innermost parentheses are removed first.

EXAMPLE 11 Nested parentheses

\begin{array}{rcl} 2 - (3 x - 2 (5 - (7 - x))) & = & 2 - (3 x - 2 (5 - 7 + x)) \\ = & 2 - (3 x - 10 + 14 - 2 x) \\ = & 2 - 3 x + 10 - 14 + 2 x = - x - 2 \end{array}

$\begin{array}{rcl} 2 - (3 x - 2 (5 - (7 - x))) & = & 2 - (3 x - 2 (5 - 7 + x)) \\ = & 2 - (3 x - 10 + 14 - 2 x) \\ = & 2 - 3 x + 10 - 14 + 2 x = - x - 2 \end{array}$

Exercises 1.7

In Exercises 1–4, make the given changes in the indicated examples of this section, and then solve the resulting problems.

In Example 6(a), change 2x to 2y.
In Example 8(a), change the sign before $(2 b - c)$ $(2 b - c)$ from $+$ $+$ to $- .$ $- .$
In Example 10(a), change $[a x - (5 s - 2 a x)]$ $[a x - (5 s - 2 a x)]$ to $[(a x - 5 s) - 2 a x] .$ $[(a x - 5 s) - 2 a x] .$
In Example 10(b), change ${[a - (2 a^{2} b - a)] + 2 b}$ ${[a - (2 a^{2} b - a)] + 2 b}$ to ${a - [2 a^{2} b - (a + 2 b)]} .$ ${a - [2 a^{2} b - (a + 2 b)]} .$

In Exercises 5–51, simplify the given algebraic expressions.

$5 x + 7 x - 4 x$ $5 x + 7 x - 4 x$
$6 t - 3 t - 4 t$ $6 t - 3 t - 4 t$
$2 y - y + 4 x$ $2 y - y + 4 x$
$- 4 C + L - 6 C$ $- 4 C + L - 6 C$
$3 t - 4 s - 3 t - s$ $3 t - 4 s - 3 t - s$
$- 8 a - b + 12 a + b$ $- 8 a - b + 12 a + b$
$2 F - 2 T - 2 + 3 F - T$ $2 F - 2 T - 2 + 3 F - T$
$x - 2 y - 3 x - y + z$ $x - 2 y - 3 x - y + z$
$a^{2} b - a^{2} b^{2} - 2 a^{2} b$ $a^{2} b - a^{2} b^{2} - 2 a^{2} b$
$- x y^{2} - 3 x^{2} y^{2} + 2 x y^{2}$ $- x y^{2} - 3 x^{2} y^{2} + 2 x y^{2}$
$2 p + (p - 6 - 2 p)$ $2 p + (p - 6 - 2 p)$
$5 + (3 - 4 n + p)$ $5 + (3 - 4 n + p)$
$v - (7 - 9 x + 2 v)$ $v - (7 - 9 x + 2 v)$
$- 2 a - \frac{1}{2} (b - a)$ $- 2 a - \frac{1}{2} (b - a)$
$2 - 3 - (4 - 5 a)$ $2 - 3 - (4 - 5 a)$
$\sqrt{A} + (h - 2 \sqrt{A}) - 3 \sqrt{A}$ $\sqrt{A} + (h - 2 \sqrt{A}) - 3 \sqrt{A}$
$(a - 3) + (5 - 6 a)$ $(a - 3) + (5 - 6 a)$
$(4 x - y) - (- 2 x - 4 y)$ $(4 x - y) - (- 2 x - 4 y)$
$- (t - 2 u) + (3 u - t)$ $- (t - 2 u) + (3 u - t)$
$- 2 (6 x - 3 y) - (5 y - 4 x)$ $- 2 (6 x - 3 y) - (5 y - 4 x)$
$3 (2 r + s) - (- 5 s - r)$ $3 (2 r + s) - (- 5 s - r)$
$3 (a - b) - 2 (a - 2 b)$ $3 (a - b) - 2 (a - 2 b)$
$- 7 (6 - 3 j) - 2 (j + 4)$ $- 7 (6 - 3 j) - 2 (j + 4)$
$- (5 t + a^{2}) - 2 (3 a^{2} - 2 s t)$ $- (5 t + a^{2}) - 2 (3 a^{2} - 2 s t)$
$- [(4 - 6 n) - (n - 3)]$ $- [(4 - 6 n) - (n - 3)]$
$- [(A - B) - (B - A)]$ $- [(A - B) - (B - A)]$
$2 [4 - (t^{2} - 5)]$ $2 [4 - (t^{2} - 5)]$
$- 3 [- 3 - \frac{2}{3} (- a - 4)]$ $- 3 [- 3 - \frac{2}{3} (- a - 4)]$
$- 2 [- x - 2 a - (a - x)]$ $- 2 [- x - 2 a - (a - x)]$
$- 2 [- 3 (x - 2 y) + 4 y]$ $- 2 [- 3 (x - 2 y) + 4 y]$
$a Z - [3 - (a Z + 4)]$ $a Z - [3 - (a Z + 4)]$
$9 v - [6 - (- v - 4) + 4 v]$ $9 v - [6 - (- v - 4) + 4 v]$
$5 z - {8 - [4 - (2 z + 1)]}$ $5 z - {8 - [4 - (2 z + 1)]}$
$7 y - {y - [2 y - (x - y)]}$ $7 y - {y - [2 y - (x - y)]}$
$5 p - (q - 2 p) - [3 q - (p - q)]$ $5 p - (q - 2 p) - [3 q - (p - q)]$
$- (4 - \sqrt{L C}) - [(5 \sqrt{L C} - 7) - (6 \sqrt{L C} + 2)]$ $- (4 - \sqrt{L C}) - [(5 \sqrt{L C} - 7) - (6 \sqrt{L C} + 2)]$
$- 2 {- (4 - x^{2}) - [3 + (4 - x^{2})]}$ $- 2 {- (4 - x^{2}) - [3 + (4 - x^{2})]}$
$- {- [- (x - 2 a) - b] - (a - x)}$ $- {- [- (x - 2 a) - b] - (a - x)}$
$5 V^{2} - (6 - (2 V^{2} + 3))$ $5 V^{2} - (6 - (2 V^{2} + 3))$
$- 2 F + 2 ((2 F - 1) - 5)$ $- 2 F + 2 ((2 F - 1) - 5)$
$- (3 t - (7 + 2 t - (5 t - 6)))$ $- (3 t - (7 + 2 t - (5 t - 6)))$
$a^{2} - 2 (x - 5 - (7 - 2 (a^{2} - 2 x) - 3 x))$ $a^{2} - 2 (x - 5 - (7 - 2 (a^{2} - 2 x) - 3 x))$
$- 4 [4 R - 2.5 (Z - 2 R) - 1.5 (2 R - Z)]$ $- 4 [4 R - 2.5 (Z - 2 R) - 1.5 (2 R - Z)]$
$- 3 {2.1 e - 1.3 [- f - 2 (e - 5 f)]}$ $- 3 {2.1 e - 1.3 [- f - 2 (e - 5 f)]}$
In determining the size of a V belt to be used with an engine, the expression $3 D - (D - d)$ $3 D - (D - d)$ is used. Simplify this expression.
When finding the current in a transistor circuit, the expression $i_{1} - (2 - 3 i_{2}) + i_{2}$ $i_{1} - (2 - 3 i_{2}) + i_{2}$ is used. Simplify this expression. (The numbers below the i’s are subscripts. Different subscripts denote different variables.)
Research on a plastic building material leads to $[(B + \frac{4}{3} α) + 2 (B - \frac{2}{3} α)] - [(B + \frac{4}{3} α) - (B - \frac{2}{3} α)] .$ $[(B + \frac{4}{3} α) + 2 (B - \frac{2}{3} α)] - [(B + \frac{4}{3} α) - (B - \frac{2}{3} α)] .$ Simplify this expression.
One car goes 30 km/h for $t - 1$ $t - 1$ hours, and a second car goes 40 km/h for $t + 2$ $t + 2$ hours. Find the expression for the sum of the distances traveled by the two cars.
A shipment contains x hard drives with 4 terabytes of memory and $x + 25$ $x + 25$ hard drives with 8 terabytes. Express the total number of terabytes of memory in the shipment as a variable expression and simplify.
Each of two suppliers has $2 n + 1$ $2 n + 1$ bundles of shingles costing $30 each and $n - 2$ $n - 2$ bundles costing $20 each. How much more is the total value of the $30 bundles than the $20 bundles?
For the expressions $2 x^{2} - y + 2 a$ $2 x^{2} - y + 2 a$ and $3 y - x^{2} - b$ $3 y - x^{2} - b$ find (a) the sum, and (b) the difference if the second is subtracted from the first.
For the following expressions, subtract the third from the sum of the first two: $3 a^{2} + b - c^{3}, 2 c^{3} - 2 b - a^{2}, 4 c^{3} - 4 b + 3.$ $3 a^{2} + b - c^{3}, 2 c^{3} - 2 b - a^{2}, 4 c^{3} - 4 b + 3.$

In Exercises 57–60, answer the given questions.

Is the following simplification correct? Explain.

$\begin{array}{rcl} 2 x - 3 y + 5 - (4 x - y + 3) & = & 2 x - 3 y + 5 - 4 x - y + 3 \\ = & - 2 x - 4 y + 8 \end{array}$ $\begin{array}{rcl} 2 x - 3 y + 5 - (4 x - y + 3) & = & 2 x - 3 y + 5 - 4 x - y + 3 \\ = & - 2 x - 4 y + 8 \end{array}$
Is the following simplification correct? Explain.

$\begin{array}{rcl} 2 a - 3 b - 4 c & - & (- 5 a + 3 b - 2 c) \\ = & 2 a - 3 b - 4 c + 5 a - 3 b - 2 c \\ = & 7 a - 6 b - 6 c \end{array}$ $\begin{array}{rcl} 2 a - 3 b - 4 c & - & (- 5 a + 3 b - 2 c) \\ = & 2 a - 3 b - 4 c + 5 a - 3 b - 2 c \\ = & 7 a - 6 b - 6 c \end{array}$
For any real numbers a and b, is it true that $| a - b | = | b - a | ?$ $| a - b | = | b - a | ?$ Explain.
Is subtraction associative? That is, in general, does $(a - b) - c$ $(a - b) - c$ equal $a - (b - c) ?$ $a - (b - c) ?$ Explain.

Answers to Practice Exercises

$6 a + 3 y$ $6 a + 3 y$
$6 r - 3 s$ $6 r - 3 s$
$5 x - 12 y$ $5 x - 12 y$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 1.7 Addition and Subtraction of Algebraic Expressions

Create new playlist

Sign In

Sign Up

Table of Contents for
1.7 Addition and Subtraction of Algebraic Expressions