17.2 Solving Linear Inequalities

  • Linear Inequalities • Inequalities with Three Members • Solving an Inequality with a Calculator

Using the properties and definitions discussed in Section 17.1, we can now proceed to solve inequalities. In this section, we solve linear inequalities in one variable. Similar to linear functions as defined in Chapter 5, a linear inequality is one in which each term contains only one variable and the exponent of each variable is 1. We will consider linear inequalities in two variables in Section 17.5.

The procedure for solving a linear inequality in one variable is similar to what we used in solving basic equations in Chapter 1. We solve the inequality by isolating the variable, and to do this we perform the same operations on each member of the inequality. The operations are based on the properties given in Section 17.1.

EXAMPLE 1 Solutions using basic operations

In each of the following inequalities, by performing the indicated operation, we isolate x and thereby solve the inequality.

x + 2 < 4Subtract 2 fromeach member.x < 2 | x2 > 4Multiply eachmember by 2.x > 8 | 2x ≤ 4Divide eachmember by 2.x ≤ 2

Each solution can be checked by substituting any number in the indicated interval into the original inequality. For example, any value less than 2 will satisfy the first inequality, whereas any number greater than 8 will satisfy the second inequality.

EXAMPLE 2 Solving a linear inequality

Solve the following inequality: 3 − 2x ≥ 15.

We have the following solution:

3  −  2x ≥ 15original inequality − 2x ≥ 12subtract 3 from each memberinequality reversed → ↓ x ≤  − 6divide each member by  − 2

CAUTION

Again, carefully note that the sign of inequality was reversed when each number was divided by  − 2.

We check the solution by substituting  − 7 in the original inequality, obtaining 17 ≥ 15.

EXAMPLE 3 Solving a linear inequality

Solve the inequality 2x ≤ 3 − x . 

The solution proceeds as follows:

2x ≤ 3 − xoriginal inequality3x ≤ 3add x to each memberx ≤ 1divide each member by 3

This solution checks and is represented in Fig. 17.7, as we showed in Section 17.1.

This inequality could have been solved by combining x-terms on the right. In doing so, we would obtain 1 ≥ x .  Because this might be misread, it is best to combine the variable terms on the left, as we did above.

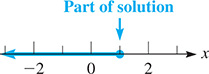
A number line with a closed circle at 1 and shading to the left. The closed circle is part of the solution.

Fig. 17.7

EXAMPLE 4 Solving a linear inequality

Solve the inequality 32(1 − x) > 14 − x . 

Illustration of steps involved in solving a linear inequality.

Note that the sense of the inequality was reversed when we divided by  − 2. This solution is shown in Fig. 17.8. Any value of x < 5/2 checks when substituted into the original inequality.

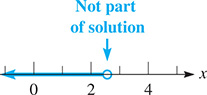
A number line with an open circle at 3 and shading to the left. The open circle is not part of the solution.

Fig. 17.8

The following example illustrates an application that involves the solution of an inequality.

EXAMPLE 5 Linear inequality—missile velocity

The velocity v (in ft/s) of a missile in terms of the time t (in s) is given by v = 960 − 32t .  For how long is the velocity positive? (Because velocity is a vector, this can also be interpreted as asking “how long is the missile moving upward?”)

In terms of inequalities, we are asked to find the values of t for which v > 0. This means that we must solve the inequality 960 − 32t > 0. The solution is as follows:

960 − 32t > 0original inequality − 32t >  − 960subtract 960 from each membert < 30 sdivide each member by  − 32

Negative values of t have no meaning in this problem. Checking t = 0 ,  we find that v = 960 ft / s .  Therefore, the complete solution is 0 ≤ t < 30 s . 

In Fig. 17.9(a), we show the graph of v = 960 − 32t ,  and in Fig. 17.9(b), we show the solution 0 ≤ t < 30 s on the number line (which is really the t-axis in this case). Note that the values of v are above the t-axis for those values of t that are part of the solution. This shows the relationship of the graph of v as a function of t, and the solution as graphed on the number line (the t-axis).

Two figures. Figure ay is a line that falls from (0, 960) through (30, 0). Figure b is a number line with shading between a closed circle at 0 and open circle at 30.

Fig. 17.9

INEQUALITIES WITH THREE MEMBERS

EXAMPLE 6 Solving inequality with three members

Solve:  − 1 < 2x + 3 < 6.

We have the following solution.

 − 1 < 2x + 3 < 6original inequality − 4 < 2x < 3subtract 3 from each member − 2 < x < 32divide each member by 2

The solution is shown in Fig. 17.10.

A number line with shading between open circles at negative 2 and 1.5.

Fig. 17.10

EXAMPLE 7 Solving inequality with three members

Solve the inequality 2x < x − 4 ≤ 3x + 8.

Since we cannot isolate x in the middle member (or in any member), we rewrite the inequality as

2x < x − 4andx − 4 ≤ 3x + 8

We then solve each of the inequalities, keeping in mind that the solution must satisfy both of them. Therefore, we have

2x < x − 4andx − 4 ≤ 3x + 8 − 2x ≤ 12x <  − 4x ≥  − 6

We see that the solution is x <  − 4 and x ≥  − 6 ,  which can also be written as  − 6 ≤ x <  − 4. This second form is generally preferred since it is more concise and more easily interpreted. The solution checks and is shown in Fig. 17.11.

A number line with shading between a closed circle at negative 6 and open circle at negative 4.

Fig. 17.11

EXAMPLE 8 Inequality with three members—pump rates

In emptying a wastewater tank, one pump can remove no more than 40 L/min. If it operates for 8.0 min and a second pump operates for 5.0 min, what must be the pumping rate of the second pump if 480 L are to be removed?

Let x = the pumping rate of the first pump and y = the pumping rate of the second pump. Because the first operates for 8.0 min and the second for 5.0 min to remove 480 L, we have

8.0xfirstpump + 5.0ysecondpump = 480total← amounts pumped

Because we know that the first pump can remove no more than 40 L/min, which means that 0 ≤ x ≤ 40 L / min, we solve for x and then substitute in this inequality:

x = 60 − 0.625ysolve for x0 ≤ 60 − 0.625y ≤ 40substitute in inequality − 60 ≤  − 0.625y ≤  − 20subtract 60 from each member96 ≥ y ≥ 32divide each member by  − 0.62532 ≤ y ≤ 96 L / minUse  ≤  symbol (optional step)

This means that the second pump must be able to pump at least 32 L/min and no more than 96 L/min. See Fig. 17.12.

A number line in liters per minute with shading between a closed circle at 32 and a closed circle at 96.

Fig. 17.12

Although this was a three-member inequality combined with equalities, the solution was done in the same way as with a two-member inequality.

SOLVING AN INEQUALITY WITH A CALCULATOR

A calculator can be used to show the solution of an inequality. On most calculators, a value of 1 is shown if the inequality is satisfied, and a value of 0 is shown if the inequality is not satisfied. This means that if, for example, we enter 8 > 3 (see the manual to see how  >  is entered), the calculator displays 1, and if we enter 3 > 8 ,  it shows 0, as in the display in Fig. 17.13. We can also use an inequality feature to show graphically the solution of an inequality.

A calculator screen with input 8 > 3, and output 1; input 3 > 8, and output 0.

Fig. 17.13

EXAMPLE 9 Inequality solution on calculator

Display the solution of the inequality 2x ≤ 3 − x (see Example 3) on a calculator.

We set y1 equal to the inequality, as shown in Fig. 17.14(a) and then graph y1 .  From Fig. 17.14(b), we see that y1 = 1 up to x = 1. Using the value feature, we can also see that y1 = 1 right at x = 1. This means the inequality is satisfied for all values of x less than or equal to 1. Thus, the solution set is x ≤ 1. Compare Fig. 17.14(b) with Fig. 17.7.

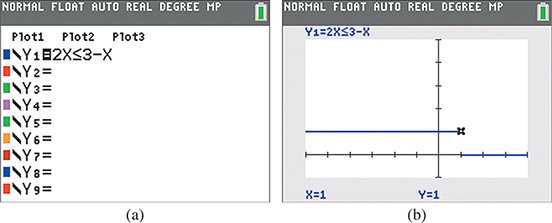
Two calculator screens. Screen ay has input y sub 1 = 2 x is less than or equal to 3 minus x. Screen b has a horizontal ray left of (1, 1).

Fig. 17.14

EXAMPLE 10 Inequality solution on calculator

Display the solution of the inequality  − 1 < 2x + 3 < 6 (see Example 6) on a calculator.

In order to display the solution, we must write the inequality as

 − 1 < 2x + 3and2x + 3 < 6see Example 7

Then enter y1 =  − 1 < 2x + 3 and 2x + 3 < 6 (consult the manual to determine how “and” is entered) in the calculator, as shown in Fig. 17.15(a). From Fig. 17.15(b), we see that the solution is  − 2 < x < 1.5. The trace and zoom features can be used to get accurate values. Compare Fig. 17.15(b) with Fig. 17.10.

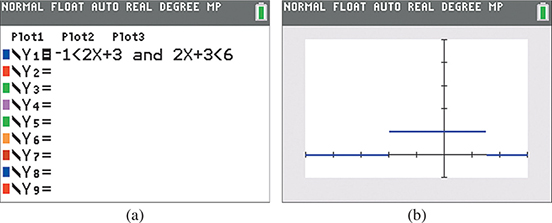
Two calculator screens. Screen ay has input y sub 1 = negative 1 < 2 x plus 3 and 2 x plus 3 < 6. Screen b has a segment from (negative 2, 1) to (1.5, 2).

Fig. 17.15

EXERCISES 17.2

In Exercises 1–4, make the given changes in the indicated examples of this section and then perform the indicated operations.

  1. In Example 2, change 3 to 25 and solve the resulting inequality.

  2. In Example 4, change the 1/4 to 7/4 and then solve and display the resulting inequality.

  3. In Example 6, change the  +  in the middle member to  −  and then solve the resulting inequality. Graph the solution.

  4. In Example 10, change the  +  in the middle member to  −  and then display the solution on a graphing calculator.

In Exercises 5–28, solve the given inequalities. Graph each solution.

  1. x − 3 >  − 4

  2. 3x + 2 ≤ 11

  3. 12x < 32

  4.  − 4t > 12

  5. 3x − 5 ≤  − 11

  6. 13x + 2 ≥ 1

  7. 12 − 2y > 16

  8. 32 − 5x <  − 8

  9. 4x − 52 ≤ x

  10. 1.5 − 5.2x ≥ 3.7 + 2.3x

  11. 180 − 6(T + 12) > 14T + 285

  12.  − 2[ x − (3 − 2x)]  > 1 − 5x3 + 2

  13. 2.50(1.50 − 3.40x) < 3.84 − 8.45x

  14. (2x − 7)(x + 1) ≤ 4 − x(1 − 2x)

  15. 13 − L2 < L + 32

  16. x5 − 2 > 23(x + 3)

  17.  − 1 ≤ 2x + 1 ≤ 3

  18. 4 < 6R + 2 ≤ 16

  19.  − 4 ≤ 1 − x <  − 1

  20. 0 ≤ 3 − 2x ≤ 6

  21. 2x < x − 1 ≤ 3x + 5

  22. x + 19 ≤ 25 − x < 2x

  23. 2s − 3 < s − 5 < 3s − 3

  24. 0 < 1 − x ≤ 3 or  − 1 < 2x − 3 < 5

In Exercises 29–38, solve the inequalities by displaying the solutions on a calculator. See Examples 9 and 10.

  1. 3x − 2 < 8 − x

  2. 40(x − 2) > x + 60

  3. 12(x + 15) ≥ 5 − 2x

  4. 13x − 2 ≤ 12x + 1

  5. 0.1 < 0.5 − 0.2t < 0.9

  6.  − 3 < 2 − s3 ≤  − 1

  7. x − 3 < 2x + 5 < 6x + 7

  8. n − 3 < 2n + 4 ≤ 1 − n

  9.  − 2(2.5x) + 5 ≥ 3

  10. ln(x − 3) ≥ 1

In Exercises 39–60, solve the given problems by setting up and solving appropriate inequalities. Graph each solution.

  1. Determine the values of x that are in the domain of the function f(x) = 2x − 10 . 

  2. Determine the values of x that are in the domain of the function f(x) = 1 / 3 − 0.5x . 

  3. For what values of k are the roots of the equation x2 − kx + 9 = 0 imaginary?

  4. For what values of k are the roots of the equation 2x2 + 3x + k = 0 real and unequal?

  5. For  − 6 < x < 2 ,  find a and b if a < 5 − x < b . 

  6. For 8 >  − x >  − 4 ,  find a and b such that a < x + 1 < b . 

  7. Insert the proper sign ( =  ,  >  ,  < ) for the ? such that | 5 − ( − 2)|  ? |  − 5 − |  − 2| |  is true.

  8. Insert the proper sign ( =  ,  >  ,  < ) for the ? such that |  − 3 − |  − 7| |  ? | |  − 3|  − 7|  is true.

  9. What range of annual interest I will give between $240 and $360 annual income from an investment of $7500?

  10. Parking at an airport costs $3.00 for the first hour, or any part thereof, and $2.50 for each additional hour, or any part thereof. What range of hours costs at least $28 and no more than $78?

  11. A contractor is considering two similar jobs, each of which is estimated to take n hours to complete. One pays $350 plus $15 per hour, and the other pays $25 per hour. For what values of n will the contractor make more at the second position?

  12. In designing plastic pipe, if the inner radius r is increased by 5.00 cm, and the inner cross-sectional area is increased by between 125 cm2 and 175 cm2 ,  what are the possible inner radii of the pipe?

  13. The relation between the temperature in degrees Fahrenheit F and degrees Celsius C is 9C = 5(F − 32) .  What temperatures F correspond to temperatures between 10°C and 20°C?

  14. The voltage drop V across a resistor is the product of the current i (in A) and the resistance R (in Ω). Find the possible voltage drops across a variable resistor R, if the minimum and maximum resistances are 1.6 k Ω and 3.6 k Ω ,  respectively, and the current is constant at 2.5 mA.

  15. A rectangular PV (photovoltaic) solar panel is designed to be 1.42 m long and supply 130 W / m2 of power. What must the width of the panel be in order to supply between 100 W and 150 W?

  16. A beam is supported at each end, as shown in Fig. 17.16. Analyzing the forces leads to the equation F1 = 13 − 3d .  For what values of d is F1 more than 6 N?

    Forces on a beam.

    Fig. 17.16

  17. The mass m (in g) of silver plate on a dish is increased by electroplating. The mass of silver on the plate is given by m = 125 + 15.0t ,  where t is the time (in h) of electroplating. For what values of t is m between 131 g and 164 g?

  18. For a ground temperature of T0 (in °C), the temperature T (in° C) at a height h (in m) above the ground is given approximately by T = T0 − 0.010h .  If the ground temperature is 25°C, for what heights is the temperature above 10°C?

  19. During a given rush hour, the numbers of vehicles shown in Fig. 17.17 go in the indicated directions in a one-way-street section of a city. By finding the possible values of x and the equation relating x and y, find the possible values of y.

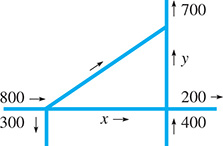
    A diagram of streets.

    Fig. 17.17

  20. The minimum legal speed on a certain interstate highway is 45 mi/h, and the maximum legal speed is 65 mi/h. What legal distances can a motorist travel in 4 h on this highway without stopping?

  21. The route of a rapid transit train is 40 km long, and the train makes five stops of equal length. If the train is actually moving for 1 h and each stop must be at least 2 min, what are the lengths of the stops if the train maintains an average speed of at least 30 km/h, including stop times?

  22. An oil company plans to install eight storage tanks, each with a capacity of x liters, and five additional tanks, each with a capacity of y liters, such that the total capacity of all tanks is 440,000 L. If capacity y will be at least 40,000 L, what are the possible values of capacity x?

Answers to Practice Exercises

  1. x < 2

  2. x < 1/6

  3. 1/4 ≤ x < 2

  4. 40 ≤ y ≤ 120 L / min

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.188.218.184