Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

11.5 Multiplication and Division of Radicals

Multiplication of Radicals • Power of a Radical • Division of Radicals • Rationalizing the Denominator

When multiplying expressions containing radicals, we use the equation $\sqrt[n]{a} \sqrt[n]{n} = \sqrt[n]{a b},$ $\sqrt[n]{a} \sqrt[n]{n} = \sqrt[n]{a b},$ along with the normal procedures of algebraic multiplication. Note that the product of two radicals can be combined only if the orders of the radicals are the same. The following examples illustrate the method.

EXAMPLE 1 Multiplying monomial radicals

$\sqrt{5} \sqrt{2} = \sqrt{5 \times 2} = \sqrt{10}$ $\sqrt{5} \sqrt{2} = \sqrt{5 \times 2} = \sqrt{10}$
.5-2 Full Alternative Text

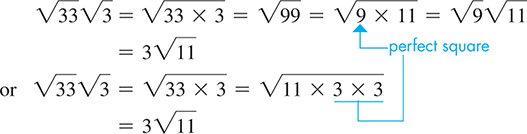
Note that we express the resulting radical in simplest form.
.5-2 Full Alternative Text

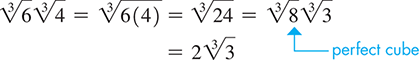
EXAMPLE 2 Multiplying binomial radicals

$\begin{array}{rcl} \sqrt{2} (3 \sqrt{5} - 4 \sqrt{2}) & = & 3 \sqrt{2} \sqrt{5} - 4 \sqrt{2} \sqrt{2} = 3 \sqrt{10} - 4 \sqrt{4} \\ = & 3 \sqrt{10} - 4 (2) = 3 \sqrt{10} - 8 \end{array}$ $\begin{array}{rcl} \sqrt{2} (3 \sqrt{5} - 4 \sqrt{2}) & = & 3 \sqrt{2} \sqrt{5} - 4 \sqrt{2} \sqrt{2} = 3 \sqrt{10} - 4 \sqrt{4} \\ = & 3 \sqrt{10} - 4 (2) = 3 \sqrt{10} - 8 \end{array}$
$\begin{array}{rcl} (5 \sqrt{7} - 2 \sqrt{3}) (4 \sqrt{7} + 3 \sqrt{3}) & = & (5 \sqrt{7}) (4 \sqrt{7}) + (5 \sqrt{7}) (3 \sqrt{3}) \\ - (2 \sqrt{3}) (4 \sqrt{7}) - (2 \sqrt{3}) (3 \sqrt{3}) \\ = & (5) (4) \sqrt{7} \sqrt{7} + (5) (3) \sqrt{7} \sqrt{3} \\ - (2) (4) \sqrt{3} \sqrt{7} - (2) (3) \sqrt{3} \sqrt{3} \\ = & 20 (7) + 15 \sqrt{21} - 8 \sqrt{21} - 6 (3) \\ = & 140 + 7 \sqrt{21} - 18 \\ = & 122 + 7 \sqrt{21} \end{array}$ $\begin{array}{rcl} (5 \sqrt{7} - 2 \sqrt{3}) (4 \sqrt{7} + 3 \sqrt{3}) & = & (5 \sqrt{7}) (4 \sqrt{7}) + (5 \sqrt{7}) (3 \sqrt{3}) \\ - (2 \sqrt{3}) (4 \sqrt{7}) - (2 \sqrt{3}) (3 \sqrt{3}) \\ = & (5) (4) \sqrt{7} \sqrt{7} + (5) (3) \sqrt{7} \sqrt{3} \\ - (2) (4) \sqrt{3} \sqrt{7} - (2) (3) \sqrt{3} \sqrt{3} \\ = & 20 (7) + 15 \sqrt{21} - 8 \sqrt{21} - 6 (3) \\ = & 140 + 7 \sqrt{21} - 18 \\ = & 122 + 7 \sqrt{21} \end{array}$

This is illustrated in the following example.

NOTE

[When raising a single-term radical expression to a power, the power can be applied to each factor of the term separately. However, when raising a binomial to a power, the entire binomial must be multiplied by itself the indicated number of times.]

EXAMPLE 3 Power of radical

${(2 \sqrt{7})}^{2} = 2^{2} {(\sqrt{7})}^{2} = 4 (7) = 28$ ${(2 \sqrt{7})}^{2} = 2^{2} {(\sqrt{7})}^{2} = 4 (7) = 28$
$\begin{array}{rcl} {(2 \sqrt{7})}^{3} & = & 2^{3} {(\sqrt{7})}^{3} = 8 {(\sqrt{7})}^{2} (\sqrt{7}) = 8 (7) \sqrt{7} \\ = & 56 \sqrt{7} \end{array}$ $\begin{array}{rcl} {(2 \sqrt{7})}^{3} & = & 2^{3} {(\sqrt{7})}^{3} = 8 {(\sqrt{7})}^{2} (\sqrt{7}) = 8 (7) \sqrt{7} \\ = & 56 \sqrt{7} \end{array}$
$\begin{array}{rcl} {(3 + \sqrt{5})}^{2} & = & (3 + \sqrt{5}) (3 + \sqrt{5}) = 9 + 3 \sqrt{5} + 3 \sqrt{5} + {(\sqrt{5})}^{2} \\ = & 9 + 6 \sqrt{5} + 5 \\ = & 14 + 6 \sqrt{5} \end{array}$ $\begin{array}{rcl} {(3 + \sqrt{5})}^{2} & = & (3 + \sqrt{5}) (3 + \sqrt{5}) = 9 + 3 \sqrt{5} + 3 \sqrt{5} + {(\sqrt{5})}^{2} \\ = & 9 + 6 \sqrt{5} + 5 \\ = & 14 + 6 \sqrt{5} \end{array}$
$\begin{array}{rcl} {(\sqrt{a} - \sqrt{b})}^{2} & = & (\sqrt{a} - \sqrt{b}) (\sqrt{a} - \sqrt{b}) = {(\sqrt{a})}^{2} - \sqrt{a b} - \sqrt{a b} + {(\sqrt{b})}^{2} \\ = & a + b - 2 \sqrt{a b} \end{array}$ $\begin{array}{rcl} {(\sqrt{a} - \sqrt{b})}^{2} & = & (\sqrt{a} - \sqrt{b}) (\sqrt{a} - \sqrt{b}) = {(\sqrt{a})}^{2} - \sqrt{a b} - \sqrt{a b} + {(\sqrt{b})}^{2} \\ = & a + b - 2 \sqrt{a b} \end{array}$

CAUTION

Again, we note that to multiply radicals and combine them under one radical sign, it is necessary that the order of the radicals be the same.

If necessary, we can make the order of each radical the same by appropriate operations on each radical separately. Fractional exponents are frequently useful for this purpose.

EXAMPLE 4 Use of fractional exponents

$\sqrt[3]{2} \sqrt{5} = 2^{1/3} 5^{1/2} = 2^{2/6} 5^{3/6} = {(2^{2} 5^{3})}^{1/6} = \sqrt[6]{500}$ $\sqrt[3]{2} \sqrt{5} = 2^{1/3} 5^{1/2} = 2^{2/6} 5^{3/6} = {(2^{2} 5^{3})}^{1/6} = \sqrt[6]{500}$
$\begin{array}{rcl} \sqrt[3]{4 a^{2} b} \sqrt[4]{8 a^{3} b^{2}} & = & {(2^{2} a^{2} b)}^{1/3} {(2^{3} a^{3} b^{2})}^{1/4} = {(2^{2} a^{2} b)}^{4/12} {(2^{3} a^{3} b^{2})}^{3/12} \\ = & {(2^{8} a^{8} b^{4})}^{1/12} {(2^{9} a^{9} b^{6})}^{1/12} = {(2^{17} a^{17} b^{10})}^{1/12} \\ = & {(2^{12} a^{12})}^{1/12} {(2^{5} a^{5} b^{10})}^{1/12} \\ = & 2 a {(2^{5} a^{5} b^{10})}^{1/12} \\ = & 2 a \sqrt[12]{32 a^{5} b^{10}} \end{array}$ $\begin{array}{rcl} \sqrt[3]{4 a^{2} b} \sqrt[4]{8 a^{3} b^{2}} & = & {(2^{2} a^{2} b)}^{1/3} {(2^{3} a^{3} b^{2})}^{1/4} = {(2^{2} a^{2} b)}^{4/12} {(2^{3} a^{3} b^{2})}^{3/12} \\ = & {(2^{8} a^{8} b^{4})}^{1/12} {(2^{9} a^{9} b^{6})}^{1/12} = {(2^{17} a^{17} b^{10})}^{1/12} \\ = & {(2^{12} a^{12})}^{1/12} {(2^{5} a^{5} b^{10})}^{1/12} \\ = & 2 a {(2^{5} a^{5} b^{10})}^{1/12} \\ = & 2 a \sqrt[12]{32 a^{5} b^{10}} \end{array}$

DIVISION OF RADICALS

If a fraction involving a radical is to be changed in form, rationalizing the denominator or rationalizing the numerator is the principal step. Although calculators have made the rationalization of denominators unnecessary for calculation, this process often makes the form of the fraction simpler. Also, rationalizing numerators is useful at times in more advanced mathematics. We now consider rationalizing when the denominator (or numerator) to be rationalized has more than one term.

NOTE

[If the denominator (or numerator) is the sum (or difference) of two terms, at least one of which is a radical, the fraction is rationalized by multiplying both the numerator and the denominator by the difference (or sum) of the same two terms, if the radicals are square roots.]

EXAMPLE 5 Rationalizing the denominator

The fraction $\frac{1}{\sqrt{3} - \sqrt{2}}$ $\frac{1}{\sqrt{3} - \sqrt{2}}$ can be rationalized by multiplying the numerator and the denominator by $\sqrt{3} + \sqrt{2} .$ $\sqrt{3} + \sqrt{2} .$ In this way, the radicals will be removed from the denominator.

An illustration depicts rationalizing the denominator of the fraction, start fraction 1 over radical 3 minus radical 2 end fraction in 3 steps.

.5-2 Full Alternative Text

The reason this technique works is that an expression of the form $a^{2} - b^{2}$ $a^{2} - b^{2}$ is created in the denominator, where a or b (or both) is a radical. We see that the result is a denominator free of radicals.

EXAMPLE 6 Rationalizing the denominator

Rationalize the denominator of $\frac{4 \sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}}$ $\frac{4 \sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}}$ and simplify the result.

An illustration depicts rationalizing the denominator of the fraction, start fraction 4 radical 6 minus radical 2, over radical 6 + radical 2 end fraction in 5 steps.

.5-2 Full Alternative Text

We note that, after rationalizing the denominator, the result has a much simpler form than the original expression.

As we noted earlier, in certain types of algebraic operations, it may be necessary to rationalize the numerator of an expression. This procedure is illustrated in the following example.

EXAMPLE 7 Rationalizing the numerator—semiconductor expression

In studying the properties of a semiconductor, the expression

\frac{C_{1} + C_{2} \sqrt{1 + 2 V}}{\sqrt{1 + 2 V}}

$\frac{C_{1} + C_{2} \sqrt{1 + 2 V}}{\sqrt{1 + 2 V}}$

is used. Here, $C_{1}$ $C_{1}$ and $C_{2}$ $C_{2}$ are constants and V is the voltage across a junction of the semiconductor. Rationalize the numerator of this expression.

Multiplying numerator and denominator by $C_{1} - C_{2} \sqrt{1 + 2 V},$ $C_{1} - C_{2} \sqrt{1 + 2 V},$ we have

\begin{array}{rcl} \frac{C_{1} + C_{2} \sqrt{1 + 2 V}}{\sqrt{1 + 2 V}} & = & \frac{(C_{1} + C_{2} \sqrt{1 + 2 V}) (C_{1} - C_{2} \sqrt{1 + 2 V})}{\sqrt{1 + 2 V} (C_{1} - C_{2} \sqrt{1 + 2 V})} \\ = & \frac{C_{1}^{2} - C_{2}^{2} {(\sqrt{1 + 2 V})}^{2}}{C_{1} \sqrt{1 + 2 V} - C_{2} \sqrt{1 + 2 V} \sqrt{1 + 2 V}} \\ = & \frac{C_{1}^{2} - C_{2}^{2} (1 + 2 V)}{C_{1} \sqrt{1 + 2 V} - C_{2} (1 + 2 V)} \end{array}

$\begin{array}{rcl} \frac{C_{1} + C_{2} \sqrt{1 + 2 V}}{\sqrt{1 + 2 V}} & = & \frac{(C_{1} + C_{2} \sqrt{1 + 2 V}) (C_{1} - C_{2} \sqrt{1 + 2 V})}{\sqrt{1 + 2 V} (C_{1} - C_{2} \sqrt{1 + 2 V})} \\ = & \frac{C_{1}^{2} - C_{2}^{2} {(\sqrt{1 + 2 V})}^{2}}{C_{1} \sqrt{1 + 2 V} - C_{2} \sqrt{1 + 2 V} \sqrt{1 + 2 V}} \\ = & \frac{C_{1}^{2} - C_{2}^{2} (1 + 2 V)}{C_{1} \sqrt{1 + 2 V} - C_{2} (1 + 2 V)} \end{array}$

Exercises11.5

In Exercises 1–4, perform the indicated operations on the resulting expressions if the given changes are made in the indicated examples of this section.

In Example 2(a), change $4 \sqrt{2}$ $4 \sqrt{2}$ to $4 \sqrt{8}$ $4 \sqrt{8}$ and then perform the multiplication.
In Example 4(a), change $\sqrt{5}$ $\sqrt{5}$ to $\sqrt{65}$ $\sqrt{65}$ and then perform the multiplication.
In Example 5, change the sign in the denominator from $-$ $-$ to $+$ $+$ and then rationalize the denominator.
In Example 6, rationalize the numerator of the given expression.

In Exercises 5–48, perform the indicated operations, expressing answers in simplest form with rationalized denominators.

$\sqrt{5} \sqrt{7}$ $\sqrt{5} \sqrt{7}$
$\sqrt{2} \sqrt{51}$ $\sqrt{2} \sqrt{51}$
$\sqrt{2} \sqrt{6}$ $\sqrt{2} \sqrt{6}$
$\sqrt{7} \sqrt{35}$ $\sqrt{7} \sqrt{35}$
$\sqrt[3]{4} \sqrt[3]{2}$ $\sqrt[3]{4} \sqrt[3]{2}$
$\sqrt[5]{4} \sqrt[5]{16}$ $\sqrt[5]{4} \sqrt[5]{16}$
${(4 \sqrt{3})}^{2}$ ${(4 \sqrt{3})}^{2}$
$2 {(3 \sqrt{5})}^{3}$ $2 {(3 \sqrt{5})}^{3}$
$\sqrt{72} \sqrt{\frac{5}{2}}$ $\sqrt{72} \sqrt{\frac{5}{2}}$
$\sqrt{\frac{6}{7}} \sqrt{\frac{2}{3}}$ $\sqrt{\frac{6}{7}} \sqrt{\frac{2}{3}}$
$\sqrt{3} (\sqrt{6} - \sqrt{5})$ $\sqrt{3} (\sqrt{6} - \sqrt{5})$
$3 \sqrt{5} (\sqrt{15} - 2 \sqrt{5})$ $3 \sqrt{5} (\sqrt{15} - 2 \sqrt{5})$
$(2 - \sqrt{5}) (2 + \sqrt{5})$ $(2 - \sqrt{5}) (2 + \sqrt{5})$
$4 {(1 - \sqrt{7})}^{2}$ $4 {(1 - \sqrt{7})}^{2}$
$(\sqrt{30} - 2 \sqrt{3}) (\sqrt{30} + 7 \sqrt{3})$ $(\sqrt{30} - 2 \sqrt{3}) (\sqrt{30} + 7 \sqrt{3})$
$(3 \sqrt{7 a} - \sqrt{50}) (\sqrt{7 a} + \sqrt{2})$ $(3 \sqrt{7 a} - \sqrt{50}) (\sqrt{7 a} + \sqrt{2})$
$(3 \sqrt{11} - \sqrt{x}) (2 \sqrt{11} + 5 \sqrt{x})$ $(3 \sqrt{11} - \sqrt{x}) (2 \sqrt{11} + 5 \sqrt{x})$
$(2 \sqrt{10} + 3 \sqrt{15}) (\sqrt{10} - 7 \sqrt{15})$ $(2 \sqrt{10} + 3 \sqrt{15}) (\sqrt{10} - 7 \sqrt{15})$
$\sqrt{a} (\sqrt{a b} + \sqrt{c^{3}})$ $\sqrt{a} (\sqrt{a b} + \sqrt{c^{3}})$
$\sqrt{3 x} (\sqrt{33 x} - \sqrt{x y})$ $\sqrt{3 x} (\sqrt{33 x} - \sqrt{x y})$
$\frac{\sqrt{6} - 9}{\sqrt{6}}$ $\frac{\sqrt{6} - 9}{\sqrt{6}}$
$\frac{5 - \sqrt{10}}{\sqrt{410}}$ $\frac{5 - \sqrt{10}}{\sqrt{410}}$
${(\sqrt{x} - 4 \sqrt{y})}^{2}$ ${(\sqrt{x} - 4 \sqrt{y})}^{2}$
$(\sqrt{c} + \sqrt{5 d}) (\sqrt{c} - \sqrt{5 d})$ $(\sqrt{c} + \sqrt{5 d}) (\sqrt{c} - \sqrt{5 d})$
$(\sqrt{2 a} - \sqrt{b}) (\sqrt{2 a} + 3 \sqrt{b})$ $(\sqrt{2 a} - \sqrt{b}) (\sqrt{2 a} + 3 \sqrt{b})$
${(2 \sqrt{m n} + 3 \sqrt{n})}^{2}$ ${(2 \sqrt{m n} + 3 \sqrt{n})}^{2}$
$\sqrt{2} \sqrt[3]{3}$ $\sqrt{2} \sqrt[3]{3}$
$\sqrt[5]{64} \sqrt[3]{16}$ $\sqrt[5]{64} \sqrt[3]{16}$
$\frac{1}{\sqrt{7} + \sqrt{3}}$ $\frac{1}{\sqrt{7} + \sqrt{3}}$
$\frac{6 \sqrt[4]{25}}{5 - 6 \sqrt{5}}$ $\frac{6 \sqrt[4]{25}}{5 - 6 \sqrt{5}}$
$\frac{\sqrt{2} - 1}{\sqrt{7} - 3 \sqrt{2}}$ $\frac{\sqrt{2} - 1}{\sqrt{7} - 3 \sqrt{2}}$
$\frac{2 \sqrt{15} - 3}{\sqrt{15} + 4}$ $\frac{2 \sqrt{15} - 3}{\sqrt{15} + 4}$
$\frac{2 \sqrt{3} - 5 \sqrt{5}}{\sqrt{3} + 2 \sqrt{5}}$ $\frac{2 \sqrt{3} - 5 \sqrt{5}}{\sqrt{3} + 2 \sqrt{5}}$
$\frac{\sqrt{15} - 3 \sqrt{5}}{2 \sqrt{15} - \sqrt{5}}$ $\frac{\sqrt{15} - 3 \sqrt{5}}{2 \sqrt{15} - \sqrt{5}}$
$\frac{6 \sqrt{x}}{\sqrt{x} - \sqrt{5}}$ $\frac{6 \sqrt{x}}{\sqrt{x} - \sqrt{5}}$
$\frac{\sqrt{5 c} + 3 d}{\sqrt{5 c} - d}$ $\frac{\sqrt{5 c} + 3 d}{\sqrt{5 c} - d}$
$(\sqrt[5]{\sqrt{6} - \sqrt{5}}) (\sqrt[5]{\sqrt{6} + \sqrt{5}})$ $(\sqrt[5]{\sqrt{6} - \sqrt{5}}) (\sqrt[5]{\sqrt{6} + \sqrt{5}})$
$\sqrt[3]{5 - \sqrt{17}} \sqrt[3]{5 + \sqrt{17}}$ $\sqrt[3]{5 - \sqrt{17}} \sqrt[3]{5 + \sqrt{17}}$
$(\sqrt{\frac{2}{R}} + \sqrt{\frac{R}{2}}) (\sqrt{\frac{2}{R}} - 2 \sqrt{\frac{R}{2}})$ $(\sqrt{\frac{2}{R}} + \sqrt{\frac{R}{2}}) (\sqrt{\frac{2}{R}} - 2 \sqrt{\frac{R}{2}})$
$(3 + \sqrt{6 - 7 a}) (2 - \sqrt{6 - 7 a})$ $(3 + \sqrt{6 - 7 a}) (2 - \sqrt{6 - 7 a})$
$\frac{\sqrt{x + y}}{\sqrt{x - y} - \sqrt{x}}$ $\frac{\sqrt{x + y}}{\sqrt{x - y} - \sqrt{x}}$
$\frac{\sqrt{1 + a}}{a - \sqrt{1 - a}}$ $\frac{\sqrt{1 + a}}{a - \sqrt{1 - a}}$
$\frac{\sqrt{a} + \sqrt{a - 2}}{\sqrt{a} - \sqrt{a - 2}}$ $\frac{\sqrt{a} + \sqrt{a - 2}}{\sqrt{a} - \sqrt{a - 2}}$
$\frac{\sqrt{T^{4} - V^{4}}}{\sqrt{V^{- 2} - T^{- 2}}}$ $\frac{\sqrt{T^{4} - V^{4}}}{\sqrt{V^{- 2} - T^{- 2}}}$

In Exercises 49–52, perform the indicated operations, expressing answers in simplest form with rationalized denominators. Then verify the result with a calculator.

$(\sqrt{11} + \sqrt{6}) (\sqrt{11} - 2 \sqrt{6})$ $(\sqrt{11} + \sqrt{6}) (\sqrt{11} - 2 \sqrt{6})$
$(2 \sqrt{5} - \sqrt{7}) (3 \sqrt{5} + \sqrt{7})$ $(2 \sqrt{5} - \sqrt{7}) (3 \sqrt{5} + \sqrt{7})$
$\frac{2 \sqrt{6} - \sqrt{5}}{3 \sqrt{6} - 4 \sqrt{5}}$ $\frac{2 \sqrt{6} - \sqrt{5}}{3 \sqrt{6} - 4 \sqrt{5}}$
$\frac{3 \sqrt{7} - 12 \sqrt{2}}{15 \sqrt{7} - 12 \sqrt{2}}$ $\frac{3 \sqrt{7} - 12 \sqrt{2}}{15 \sqrt{7} - 12 \sqrt{2}}$

In Exercises 53–56, combine the terms into a single fraction, but do not rationalize the denominators.

$2 \sqrt{x} + \frac{1}{\sqrt{x}}$ $2 \sqrt{x} + \frac{1}{\sqrt{x}}$
$\frac{3}{2 \sqrt{3 x - 4}} - \sqrt{3 x - 4}$ $\frac{3}{2 \sqrt{3 x - 4}} - \sqrt{3 x - 4}$
$\frac{x^{2}}{\sqrt{2 x + 1}} + 2 x \sqrt{2 x + 1}$ $\frac{x^{2}}{\sqrt{2 x + 1}} + 2 x \sqrt{2 x + 1}$
$4 \sqrt{x^{2} + 1} - \frac{4 x}{\sqrt{x^{2} + 1}}$ $4 \sqrt{x^{2} + 1} - \frac{4 x}{\sqrt{x^{2} + 1}}$

In Exercises 57–60, rationalize the numerator of each fraction.

$\frac{\sqrt{5} + 2 \sqrt{2}}{3 \sqrt{10}}$ $\frac{\sqrt{5} + 2 \sqrt{2}}{3 \sqrt{10}}$
$\frac{\sqrt{19} - 3}{5}$ $\frac{\sqrt{19} - 3}{5}$
$\frac{\sqrt{x + h} - \sqrt{x}}{h}$ $\frac{\sqrt{x + h} - \sqrt{x}}{h}$
$\frac{\sqrt{3 x + 4} + \sqrt{3 x}}{8}$ $\frac{\sqrt{3 x + 4} + \sqrt{3 x}}{8}$

In Exercises 61–76, solve the given problems.

Are there any values of x or y such that $\sqrt{x} + \sqrt{y} = \sqrt{x + y} ?$ $\sqrt{x} + \sqrt{y} = \sqrt{x + y} ?$
For what real values of x and y is $\sqrt[3]{x} + \sqrt[3]{y} = \sqrt[3]{x + y} ?$ $\sqrt[3]{x} + \sqrt[3]{y} = \sqrt[3]{x + y} ?$
By substitution, show that $x = 1 - \sqrt{2}$ $x = 1 - \sqrt{2}$ is a solution of the equation $x^{2} - 2 x - 1 = 0.$ $x^{2} - 2 x - 1 = 0.$
For the quadratic equation $a x^{2} + b x + c = 0,$ $a x^{2} + b x + c = 0,$ if a, b, and c are integers, the product of the roots is a rational number. Explain.
Determine the relationship between a and c in $a x^{2} + b x + c = 0$ $a x^{2} + b x + c = 0$ if the roots of the equation are reciprocals.
Evaluate $r^{2} - s^{2}$ $r^{2} - s^{2}$ if $r = - b + \sqrt{b^{2} - 4 a c}$ $r = - b + \sqrt{b^{2} - 4 a c}$ and $s = - b - \sqrt{b^{2} - 4 a c} .$ $s = - b - \sqrt{b^{2} - 4 a c} .$
Rationalize the denominator of $\frac{1}{\sqrt[3]{x^{2}} + \sqrt[3]{x} + 1}$ $\frac{1}{\sqrt[3]{x^{2}} + \sqrt[3]{x} + 1}$ by using the equation $a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2}) .$ $a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2}) .$ (Hint: The denominator is of the form $a^{2} + a b + b^{2} .$ $a^{2} + a b + b^{2} .$ )
One leg of a right triangle is $2 \sqrt{7}$ $2 \sqrt{7}$ and the hypotenuse is 6. What is the area of the triangle?
For an object oscillating at the end of a spring and on which there is a force that retards the motion, the equation $m^{2} + b m + k^{2} = 0$ $m^{2} + b m + k^{2} = 0$ must be solved. Here, b is a constant related to the retarding force, and k is the spring constant. By substitution, show that $m = \frac{1}{2} (\sqrt{b^{2} - 4 k^{2}} - b)$ $m = \frac{1}{2} (\sqrt{b^{2} - 4 k^{2}} - b)$ is a solution.
Among the products of a specialty furniture company are tables with tops in the shape of a regular octagon (eight sides). Express the area A of a table top as a function of the side s of the octagon.
An expression used in determining the characteristics of a spur gear is $\frac{50}{50 + \sqrt{V}} .$ $\frac{50}{50 + \sqrt{V}} .$ Rationalize the denominator.
When studying the orbits of Earth satellites, the expression ${(\frac{G M}{4 π^{2}})}^{1/3} T^{2/3}$ ${(\frac{G M}{4 π^{2}})}^{1/3} T^{2/3}$ arises. Express it in simplest rationalized radical form.
In analyzing a tuned amplifier circuit, the expression $\frac{2 Q}{\sqrt{\sqrt{2} - 1}}$ $\frac{2 Q}{\sqrt{\sqrt{2} - 1}}$ is used. Rationalize the denominator.
When analyzing the ratio of resultant forces when forces F and T act on a structure, the expression $\sqrt{F^{2} + T^{2}} / \sqrt{F^{- 2} + T^{- 2}}$ $\sqrt{F^{2} + T^{2}} / \sqrt{F^{- 2} + T^{- 2}}$ arises. Simplify this expression.
The resonant frequency $ω$ $ω$ of a capacitance C in parallel with a resistance R and inductance L (see Fig. 11.9) is

$ω = \frac{1}{\sqrt{L C}} \sqrt{1 - \frac{R^{2} C}{L}} .$ $ω = \frac{1}{\sqrt{L C}} \sqrt{1 - \frac{R^{2} C}{L}} .$

Combine terms under the radical, rationalize the denominator, and simplify.

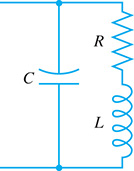
Fig. 11.9
In fluid dynamics, the expression $\frac{a}{1 + m / \sqrt{r}}$ $\frac{a}{1 + m / \sqrt{r}}$ arises. Combine terms in the denominator, rationalize the denominator, and simplify.

Answers to Practice Exercises

$7 \sqrt{2}$ $7 \sqrt{2}$
$10 \sqrt{3} - 6 \sqrt{15}$ $10 \sqrt{3} - 6 \sqrt{15}$
$30 + 3 \sqrt{2}$ $30 + 3 \sqrt{2}$
$\frac{- 48 + 25 \sqrt{3}}{143}$ $\frac{- 48 + 25 \sqrt{3}}{143}$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 11.5 Multiplication and Division of Radicals

Create new playlist

Sign In

Sign Up

Table of Contents for
11.5 Multiplication and Division of Radicals