Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

6.2 Factoring Trinomials

Factoring Trinomials with Leading Coefficient of 1 • Factoring General Trinomials by Trial and Error • Factoring General Trinomials by Grouping • Factoring Perfect Square Trinomials • Factoring Completely

In Section 6.1, we saw that factoring expressions can be viewed as the reverse of multiplication. In this section, we apply this same idea to expressions with three terms, called trinomials. In order to factor trinomials, we must first understand the process by which two binomials are multiplied, and then reverse that process. In other words, we have to find two binomials that, when multiplied together, will equal the given trinomial. We begin with the simplest case, which is factoring trinomials in which the coefficient of $x^{2},$ $x^{2},$ called the leading coefficient, is 1.

FACTORING TRINOMIALS WITH A LEADING COEFFICIENT OF 1

Recall that when two binomials are multiplied, each term in the first binomial is multiplied by each term in the second. Therefore,

(x + a) (x + b) = x^{2} + a x + b x + a b = x^{2} + (a + b) x + a b

$(x + a) (x + b) = x^{2} + a x + b x + a b = x^{2} + (a + b) x + a b$

This result gives us the following special product:

(x + a) (x + b) = x^{2} + (a + b) x + a b

$(x + a) (x + b) = x^{2} + (a + b) x + a b$

(6.4)

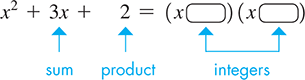
Notice that the coefficient of x is the sum of a and b and the last term is the product of a and b. Reversing this process will allow us to factor a trinomial when the coefficient of $x^{2}$ $x^{2}$ is 1 as shown in the diagram below:

x squared + left parenthesis a + b right parenthesis x + a b = left parenthesis x + a right parenthesis left parenthesis x + b right parenthesis. Where x squared coefficient is 1, + is sum, and a b is product.

Essentially, we need to find two integers that have a product equal to the last term of a given trinomial and a sum equal to the coefficient of x. Once we find these two integers, we insert them into the following product to get the factored form: .

EXAMPLE 1 Factoring trinomial x² + (a + b )x + ab

In factoring $x^{2} + 3 x + 2,$ $x^{2} + 3 x + 2,$ we set it up as

X squared + 3 x + 2 = left parenthesis x, empty box right parenthesis x empty box right parenthesis. Where 3 x is sum, 2 is product, and empty boxes are integers.

The constant 2 tells us that the product of the required integers is 2. Thus, the only possibilities are 2 and 1 (or 1 and 2). The $+$ $+$ sign before the 2 indicates that the sign before the 1 and 2 in the factors must be the same. The $+$ $+$ sign before the 3, the sum of the integers, tells us that both signs are positive. Therefore,

x^{2} + 3 x + 2 = (x + 2) (x + 1)

$x^{2} + 3 x + 2 = (x + 2) (x + 1)$

In factoring $x^{2} - 3 x + 2,$ $x^{2} - 3 x + 2,$ the analysis is the same until we note that the middle term is negative. This tells us that both signs are negative in this case. Therefore,

x^{2} - 3 x + 2 = (x - 2) (x - 1)

$x^{2} - 3 x + 2 = (x - 2) (x - 1)$

For a trinomial with first term $x^{2}$ $x^{2}$ and constant $+ 2$ $+ 2$ to be factorable, the middle term must be $+ 3 x$ $+ 3 x$ or $- 3 x$ $- 3 x$ . No other middle terms are possible. This means, for example, the expressions $x^{2} + 4 x + 2$ $x^{2} + 4 x + 2$ and $x^{2} - x + 2$ $x^{2} - x + 2$ cannot be factored.

EXAMPLE 2 Factoring trinomials x² + (a + b )x + ab

In order to factor $x^{2} + 7 x - 8,$ $x^{2} + 7 x - 8,$ we must find two integers whose product is $- 8$ $- 8$ and whose sum is $+ 7.$ $+ 7.$ The possible factors of $- 8$ $- 8$ are

$- 8 and + 1 + 8 and - 1 - 4 and + 2 + 4 and - 2$ $- 8 and + 1 + 8 and - 1 - 4 and + 2 + 4 and - 2$

Inspecting these, we see that only $+ 8$ $+ 8$ and $- 1$ $- 1$ have the sum of $+ 7.$ $+ 7.$ Therefore,

$x^{2} + 7 x - 8 = (x + 8) (x - 1)$ $x^{2} + 7 x - 8 = (x + 8) (x - 1)$

In choosing the correct values for the integers, it is usually fairly easy to find a pair for which the product is the final term. However, choosing the pair of integers that correctly fits the middle term is the step that often is not done properly. Special attention must be given to choosing the integers so that the expansion of the resulting factors has the correct middle term of the original expression.

Always multiply the factors together to check to see that you get the correct middle term.
In the same way, we have

$x^{2} - x - 12 = (x - 4) (x + 3)$ $x^{2} - x - 12 = (x - 4) (x + 3)$

because $- 4$ $- 4$ and $+ 3$ $+ 3$ is the only pair of integers whose product is $- 12$ $- 12$ and whose sum is $- 1.$ $- 1.$
Also,

$x^{2} - 5 x y + 6 y^{2} = (x - 3 y) (x - 2 y)$ $x^{2} - 5 x y + 6 y^{2} = (x - 3 y) (x - 2 y)$

because $- 3$ $- 3$ and $- 2$ $- 2$ is the only pair of integers whose product is $+ 6$ $+ 6$ and whose sum is $- 5.$ $- 5.$ Here, we find second terms of each factor with a product of $6 y^{2}$ $6 y^{2}$ and sum of $- 5 x y,$ $- 5 x y,$ which means that each second term must have a factor of y, as we have shown above.

FACTORING GENERAL TRINOMIALS BY TRIAL AND ERROR

We will now turn our attention to factoring general trinomials, where the coefficient of the squared term can be any integer (not just 1 as in the previous examples). Let us first review the process by which two general binomials are multiplied:

(a x + b) (c x + d) = a c x^{2} + a d x + b c x + b d

$(a x + b) (c x + d) = a c x^{2} + a d x + b c x + b d$

(a x + b) (c x + d) = a c x^{2} + (a d + b c) x + b d

$(a x + b) (c x + d) = a c x^{2} + (a d + b c) x + b d$

(6.5)

Rewriting Eq. (6.5) with the sides reversed gives us a strategy for factoring general trinomials by trial and error as shown in the diagram below:

.2-2 Full Alternative Text

This diagram shows us that

the coefficient of $x^{2}$ $x^{2}$ is the product of the coefficients a and c in the factors,
the final constant is the product of the constants b and d in the factors, and
the coefficient of x is the sum of the inner and outer products.

CAUTION

In finding the factors, we must try possible combinations of a, b, c, and d that give the proper inner and outer products for the middle term of the given expression. This requires some trial and error as shown in the following examples.

EXAMPLE 3 Factoring a general trinomial by trial and error

To factor $2 x^{2} + 11 x + 5,$ $2 x^{2} + 11 x + 5,$ we take the factors of 2 to be $+ 2$ $+ 2$ and $+ 1$ $+ 1$ (we use only positive coefficients a and c when the coefficient of $x^{2}$ $x^{2}$ is positive). We set up the factoring as

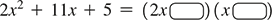
Because the product of the integers to be found is $+ 5,$ $+ 5,$ only integers of the same sign need to be considered. The factors of $+ 5$ $+ 5$ are $+ 1$ $+ 1$ and $+ 5,$ $+ 5,$ and $- 1$ $- 1$ and $- 5,$ $- 5,$ which means that $+ 1$ $+ 1$ and $+ 5$ $+ 5$ is the only possible pair. Now, trying the factors

NOTE

[Also because the sum of the outer and inner products is $+ 11,$ $+ 11,$ the integers are positive.]

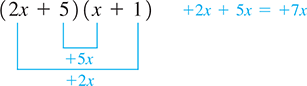
Left parenthesis 2 x + 5 right parenthesis, left parenthesis x + 1 right parenthesis. the 5 in is + 5 x. the 2 x in 2 x + 5 and the 1 in x + 1 is + 2 x. + 2 x + 5 x = + 7 x.

we see that 7x is not the correct middle term.

Therefore, we now try

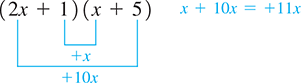
Left parenthesis 2 x + 1 right parenthesis left parenthesis x + 5 right parenthesis. the 1 in 2 x + 1 and the x in x + 5 is + x. the 2 x in 2 x + 1 and the 5 in x + 5 is + 10 x.

and we have the correct sum of $+ 11 x$ $+ 11 x$ . Therefore,

2 x^{2} + 11 x + 5 = (2 x + 1) (x + 5)

$2 x^{2} + 11 x + 5 = (2 x + 1) (x + 5)$

For a trinomial with a first term $2 x^{2}$ $2 x^{2}$ and a constant $+ 5$ $+ 5$ to be factorable, we can now see that the middle term must be either $\pm 11 x$ $\pm 11 x$ or $\pm 7 x$ $\pm 7 x$ . This means that $2 x^{2} + 7 x + 5 = (2 x + 5) (x + 1),$ $2 x^{2} + 7 x + 5 = (2 x + 5) (x + 1),$ but a trinomial such as $2 x^{2} + 8 x + 5$ $2 x^{2} + 8 x + 5$ is not factorable.

EXAMPLE 4 Factoring a general trinomial by trial and error

In factoring $4 x^{2} + 4 x - 3,$ $4 x^{2} + 4 x - 3,$ the coefficient 4 in $4 x^{2}$ $4 x^{2}$ shows that the possible coefficients of x in the factors are 4 and 1, or 2 and 2. This gives us the following possible combinations of factors, along with the resulting sum of the outer and inner products:

NOTE

[The 3 shows that the only possible constants in the factors are 1 and 3, and the minus sign with the 3 tells us that these integers have different signs.]

\begin{array}{l} (4 x + 3) (x - 1) : - 4 x + 3 x = - x \\ (4 x + 1) (x - 3) : - 12 x + x = - 11 x \\ (4 x - 3) (x + 1) : 4 x - 3 x = + x \\ (4 x - 1) (x + 3) : 12 x - x = + 11 x \\ (2 x + 3) (2 x - 1) : - 2 x + 6 x = + 4 x \\ (2 x - 3) (2 x + 1) : 2 x - 6 x = - 4 x \end{array}

$\begin{array}{l} (4 x + 3) (x - 1) : - 4 x + 3 x = - x \\ (4 x + 1) (x - 3) : - 12 x + x = - 11 x \\ (4 x - 3) (x + 1) : 4 x - 3 x = + x \\ (4 x - 1) (x + 3) : 12 x - x = + 11 x \\ (2 x + 3) (2 x - 1) : - 2 x + 6 x = + 4 x \\ (2 x - 3) (2 x + 1) : 2 x - 6 x = - 4 x \end{array}$

We see that the factors that have the correct middle term of $+ 4 x$ $+ 4 x$ are $(2 x + 3) (2 x - 1)$ $(2 x + 3) (2 x - 1)$ . This means that

.2-3 Full Alternative Text

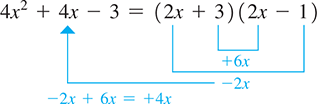
Expressing the result with the factors reversed is an equally correct answer.

NOTE

[Another hint given by the coefficients of the original expression is that the plus sign with the 4x tells us that the larger of the outer and inner products must be positive.]

EXAMPLE 5 Factoring a general trinomial—beam deflection

An expression that arises when analyzing the deflection of beams is $9 x^{2} - 32 L x + 28 L^{2}$ $9 x^{2} - 32 L x + 28 L^{2}$ . When factoring this expression, we get

9 x^{2} - 32 L x + 28 L^{2} = (x - 2 L) (9 x - 14 L)

$9 x^{2} - 32 L x + 28 L^{2} = (x - 2 L) (9 x - 14 L)$

NOTE

[There are numerous possible combinations for 9 and 28, but we must carefully check that the middle term is the sum of the inner and outer products of the factors we have chosen.]

- 14 L x - 18 L x = - 32 L x checking middle term

$- 14 L x - 18 L x = - 32 L x checking middle term$

FACTORING GENERAL TRINOMIALS BY GROUPING

Sometimes when using trial and error, there are many possible combinations of values to try and it can be difficult to find the ones that result in the correct middle term. We now discuss another alternative for factoring general trinomials, which utilizes factoring by grouping. In Section 6.1, we saw that we could sometimes factor an expression containing four terms by grouping the first two terms and the last two terms. This same technique can be applied to trinomials of the form $a x^{2} + b x + c$ $a x^{2} + b x + c$ if we first split up the x-term into two terms using the method described below:

Find the product ac.
Find two numbers whose product is ac and whose sum is b.
Replace the middle term bx with two x-terms having these numbers as coefficients.
Complete the factorization by grouping.

This method is sometimes referred to as “ ac splits b.” The following example illustrates how this is done.

EXAMPLE 6 Factoring a general trinomial by grouping

Factor the trinomial $3 x^{2} - 10 x y + 8 y^{2}$ $3 x^{2} - 10 x y + 8 y^{2}$ .

We start by finding the product $a c = 3 (8) = 24.$ $a c = 3 (8) = 24.$ Next, we find two numbers that have a product of 24 and a sum of $- 10.$ $- 10.$ The two numbers that work are $- 6$ $- 6$ and $- 4.$ $- 4.$ We use these numbers as coefficients to split up the middle term and then factor by grouping.

\begin{aligned} 3 x^{2} - 10 x y + 8 y^{2} & = & 3 x^{2} - 6 x y - 4 x y + 8 y^{2} & - 10 x y = - 6 x y - 4 x y \\ = & 3 x (x - 2 y) \underline{?} (x - 2 y) & \begin{matrix} Factor out the GCF 3 x from the \\ first two terms . Since the second \\ set of parentheses must match the \\ first, determine the expression to \\ factor out of the second two terms . \end{matrix} \\ = & 3 x (x - 2 y) - 4 y (x - 2 y) & The required expression is - 4 y . \\ = & (x - 2 y) (3 x - 4 y) & \begin{array}{l} Factor out the common binomial \\ factor (x - 2 y) . \end{array} \end{aligned}

$\begin{aligned} 3 x^{2} - 10 x y + 8 y^{2} & = & 3 x^{2} - 6 x y - 4 x y + 8 y^{2} & - 10 x y = - 6 x y - 4 x y \\ = & 3 x (x - 2 y) \underline{?} (x - 2 y) & \begin{matrix} Factor out the GCF 3 x from the \\ first two terms . Since the second \\ set of parentheses must match the \\ first, determine the expression to \\ factor out of the second two terms . \end{matrix} \\ = & 3 x (x - 2 y) - 4 y (x - 2 y) & The required expression is - 4 y . \\ = & (x - 2 y) (3 x - 4 y) & \begin{array}{l} Factor out the common binomial \\ factor (x - 2 y) . \end{array} \end{aligned}$

NOTE

[It is important to note that when splitting the middle term, the two terms can be inserted in either order.]

For example, replacing $- 10 x y$ $- 10 x y$ with $- 4 x y - 6 x y$ $- 4 x y - 6 x y$ would lead to an equivalent answer, although the factors may be in a different order.

To summarize, a general trinomial can be factored either by trial and error or by grouping. Either method can be used, depending on one's preference.

FACTORING PERFECT SQUARE TRINOMIALS

Some trinomials factor into two identical factors. For example, $x^{2} + 6 x + 9 = (x + 3) (x + 3) = {(x + 3)}^{2}$ $x^{2} + 6 x + 9 = (x + 3) (x + 3) = {(x + 3)}^{2}$ . Trinomials that factor in this way are called perfect square trinomials. If we recognize a perfect square trinomial, then it is much easier to factor since we know the two factors must be the same. The two special products below show the form of a perfect square trinomial.

{(a + b)}^{2} = a^{2} + 2 a b + b^{2}

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

(6.6)

{(a - b)}^{2} = a^{2} - 2 a b + b^{2}

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

(6.7)

Notice that the first and last terms of Eqs. (6.6) and (6.7) are both perfect squares. When we encounter a trinomial in which the first and last terms are perfect squares, there is a possibility that it is a perfect square trinomial, but we must also check the middle term as demonstrated in the following example.

EXAMPLE 7 Checking for perfect square trinomials

In factoring $x^{2} + 12 x + 36,$ $x^{2} + 12 x + 36,$ we should notice that the first term is the square of x and the last term is the square of 6. Therefore, this might be a perfect square trinomial and factor into two identical factors. It is wise to try this possibility first and see if the inner and outer products combine to equal the middle term:

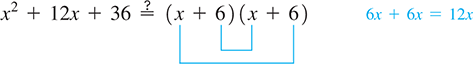
Since the middle term checks, we have the correct factorization, which can be written as ${(x + 6)}^{2}$ ${(x + 6)}^{2}$ .
In factoring $36 x^{2} - 84 x y + 49 y^{2},$ $36 x^{2} - 84 x y + 49 y^{2},$ notice that the first term is the square of 6x and the last term is the square of 7y. We will check the middle term to see if this is a perfect square trinomial:

.2-3 Full Alternative Text

Since the middle term checks, we have the correct factorization, which is ${(6 x - 7 y)}^{2}$ ${(6 x - 7 y)}^{2}$ . This expression would have been much more difficult to factor if we had used either the trial-and-error method (without recognizing it as a perfect square trinomial) or the grouping method.
In factoring $4 x^{2} - 25 x + 25,$ $4 x^{2} - 25 x + 25,$ notice the first term is the square of 2x and the last term is the square of 5. To see if this is a perfect square trinomial, we again check the middle term:

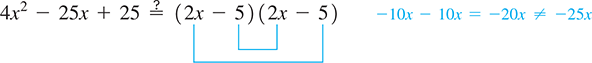
The middle term does not check, so we do not have the correct factorization. When factored correctly using either trial and error or grouping, we find that $4 x^{2} - 25 x + 25 = (4 x - 5) (x - 5)$ $4 x^{2} - 25 x + 25 = (4 x - 5) (x - 5)$ .

CAUTION

Example 7(c) demonstrates an important point. Just because the first and last terms of a trinomial are perfect squares, we can’t assume the expression is a perfect square trinomial. We must check the middle term.

FACTORING COMPLETELY

As mentioned in the previous section, it is important that we factor expressions completely. To do this, first factor out the greatest common factor (if possible), and then attempt to further factor the remaining expression.

EXAMPLE 8 Factoring completely

When factoring $2 x^{2} + 6 x - 8,$ $2 x^{2} + 6 x - 8,$ first note the common factor of 2. This leads to

2 x^{2} + 6 x - 8 = 2 (x^{2} + 3 x - 4)

$2 x^{2} + 6 x - 8 = 2 (x^{2} + 3 x - 4)$

Now, notice that $x^{2} + 3 x - 4$ $x^{2} + 3 x - 4$ is also factorable. Therefore,

2 x^{2} + 6 x - 8 = 2 (x + 4) (x - 1)

$2 x^{2} + 6 x - 8 = 2 (x + 4) (x - 1)$

CAUTION

If you attempt to factor the previous example without first factoring out the common factor of 2, it becomes much more difficult, and also the result will not be factored completely. There would still be a common factor inside the parentheses, so additional steps would be needed. It is always easier to factor out the greatest common factor first.

EXAMPLE 9 Factoring completely—rocket flight

A study of the path of a certain rocket leads to the expression $16 t^{2} + 240 t - 1600,$ $16 t^{2} + 240 t - 1600,$ where t is the time of flight. Factor this expression.

An inspection shows that there is a common factor of 16. Factoring out 16 leads to

\begin{array}{l} 16 t^{2} + 240 t - 1600 = 16 (t^{2} + 15 t - 100) \\ = 16 (t + 20) (t - 5) \end{array}

$\begin{array}{l} 16 t^{2} + 240 t - 1600 = 16 (t^{2} + 15 t - 100) \\ = 16 (t + 20) (t - 5) \end{array}$

Note that by first factoring out the common factor of 16, the resulting trinomial $t^{2} + 15 t - 100$ $t^{2} + 15 t - 100$ is much easier to factor than the original trinomial $16 t^{2} + 240 t - 1600.$ $16 t^{2} + 240 t - 1600.$

EXERCISES 6.2

In Exercises 1–4, make the given changes in the indicated examples of this section and then factor.

In Example 1, change the 3 to 4 and the 2 to 3.
In Example 2(a), change the $+$ $+$ before 7x to $-$ $-$ .
In Example 3, change the $+$ $+$ before 11x to $-$ $-$ .
In Example 8, change the 8 to 36.

In Exercises 5–8, find each product.

${(x - 7)}^{2}$ ${(x - 7)}^{2}$
${(y + 6)}^{2}$ ${(y + 6)}^{2}$
${(a + 3 b)}^{2}$ ${(a + 3 b)}^{2}$
${(2 n + 5 m)}^{2}$ ${(2 n + 5 m)}^{2}$

In Exercises 9–54, factor the given expressions completely.

$x^{2} + 4 x + 3$ $x^{2} + 4 x + 3$
$x^{2} - 5 x - 6$ $x^{2} - 5 x - 6$
$s^{2} - s - 42$ $s^{2} - s - 42$
$a^{2} + 14 a - 32$ $a^{2} + 14 a - 32$
$t^{2} + 5 t - 24$ $t^{2} + 5 t - 24$
$r^{3} - 11 r^{2} + 18 r$ $r^{3} - 11 r^{2} + 18 r$
$x^{2} + 8 x + 16$ $x^{2} + 8 x + 16$
$D^{2} + 8 D + 16$ $D^{2} + 8 D + 16$
$a^{2} - 6 a b + 9 b^{2}$ $a^{2} - 6 a b + 9 b^{2}$
$b^{2} - 12 b c + 36 c^{2}$ $b^{2} - 12 b c + 36 c^{2}$
$3 x^{2} - 5 x - 2$ $3 x^{2} - 5 x - 2$
$6 n^{2} - 39 n - 21$ $6 n^{2} - 39 n - 21$
$12 y^{2} - 32 y - 12$ $12 y^{2} - 32 y - 12$
$25 x^{2} + 45 x - 10$ $25 x^{2} + 45 x - 10$
$2 s^{2} + 13 s + 11$ $2 s^{2} + 13 s + 11$
$5 - 12 y + 7 y^{2}$ $5 - 12 y + 7 y^{2}$
$3 z^{2} - 19 z + 6$ $3 z^{2} - 19 z + 6$
$10 R^{4} - 6 R^{2} - 4$ $10 R^{4} - 6 R^{2} - 4$
$2 t^{2} + 7 t - 15$ $2 t^{2} + 7 t - 15$
$20 - 20 n + 3 n^{2}$ $20 - 20 n + 3 n^{2}$
$3 t^{2} - 7 t u + 4 u^{2}$ $3 t^{2} - 7 t u + 4 u^{2}$
$3 x^{2} + x y - 14 y^{2}$ $3 x^{2} + x y - 14 y^{2}$
$6 x^{2} + x - 5$ $6 x^{2} + x - 5$
$2 z^{2} + 13 z - 5$ $2 z^{2} + 13 z - 5$
$9 x^{2} + 7 x y - 2 y^{2}$ $9 x^{2} + 7 x y - 2 y^{2}$
$4 r^{2} + 11 r s - 3 s^{2}$ $4 r^{2} + 11 r s - 3 s^{2}$
$12 m^{2} + 60 m + 75$ $12 m^{2} + 60 m + 75$
$48 q^{2} + 72 q + 27$ $48 q^{2} + 72 q + 27$
$8 x^{2} - 24 x + 18$ $8 x^{2} - 24 x + 18$
$3 a^{2} c^{2} - 6 a c + 3$ $3 a^{2} c^{2} - 6 a c + 3$
$9 t^{2} - 15 t + 4$ $9 t^{2} - 15 t + 4$
$6 t^{4} + t^{2} - 12$ $6 t^{4} + t^{2} - 12$
$8 b^{6} + 31 b^{3} - 4$ $8 b^{6} + 31 b^{3} - 4$
$12 n^{4} + 8 n^{2} - 15$ $12 n^{4} + 8 n^{2} - 15$
$4 p^{2} - 25 p q + 6 q^{2}$ $4 p^{2} - 25 p q + 6 q^{2}$
$12 x^{2} + 4 x y - 5 y^{2}$ $12 x^{2} + 4 x y - 5 y^{2}$
$12 x^{2} + 47 x y - 4 y^{2}$ $12 x^{2} + 47 x y - 4 y^{2}$
$8 r^{2} - 14 r s - 9 s^{2}$ $8 r^{2} - 14 r s - 9 s^{2}$
$12 - 14 x + 2 x^{2}$ $12 - 14 x + 2 x^{2}$
$6 y^{2} - 33 y - 18$ $6 y^{2} - 33 y - 18$
$4 x^{5} + 14 x^{3} - 8 x$ $4 x^{5} + 14 x^{3} - 8 x$
$12 B^{2} + 22 B H - 4 H^{2}$ $12 B^{2} + 22 B H - 4 H^{2}$
$a x^{3} + 4 a^{2} x^{2} - 12 a^{3} x$ $a x^{3} + 4 a^{2} x^{2} - 12 a^{3} x$
$15 x^{2} - 39 x^{3} + 18 x^{4}$ $15 x^{2} - 39 x^{3} + 18 x^{4}$
$4 x^{2 n} + 13 x^{n} - 12$ $4 x^{2 n} + 13 x^{n} - 12$
$12 B^{2 n} + 19 B^{n} H - 10 H^{2}$ $12 B^{2 n} + 19 B^{n} H - 10 H^{2}$

In Exercises 55–66, factor the given expressions completely. Each is from the technical area indicated.

$16 t^{2} - 80 t + 64$ $16 t^{2} - 80 t + 64$ (projectile motion)
$9 x^{2} - 33 L x + 30 L^{2}$ $9 x^{2} - 33 L x + 30 L^{2}$ (civil engineering)
$d^{4} - 10 d^{2} + 16$ $d^{4} - 10 d^{2} + 16$ (magnetic field)
$3 e^{2} + 18 e - 1560$ $3 e^{2} + 18 e - 1560$ (fuel efficiency)
$3 Q^{2} + Q - 30$ $3 Q^{2} + Q - 30$ (fire science)
$b T^{2} - 40 b T + 400 b$ $b T^{2} - 40 b T + 400 b$ (thermodynamics)
$V^{2} - 2 n B V + n^{2} B^{2}$ $V^{2} - 2 n B V + n^{2} B^{2}$ (chemistry)
$a^{4} + 8 a^{2} π^{2} f^{2} + 16 π^{4} f^{4}$ $a^{4} + 8 a^{2} π^{2} f^{2} + 16 π^{4} f^{4}$ (periodic motion: energy)
$w x^{4} - 5 w L x^{3} + 6 w L^{2} x^{2}$ $w x^{4} - 5 w L x^{3} + 6 w L^{2} x^{2}$ (beam design)
$1 - 2 r^{2} + r^{4}$ $1 - 2 r^{2} + r^{4}$ (lasers)
$3 A d u^{2} - 4 A d u v + A d v^{2}$ $3 A d u^{2} - 4 A d u v + A d v^{2}$ (water power)
$k^{2} A^{2} + 2 k λ A + λ^{2} - α^{2}$ $k^{2} A^{2} + 2 k λ A + λ^{2} - α^{2}$ (robotics)

In Exercises 67–70, solve the given problems.

Find the two integer values of k that make $4 x^{2} + k x + 9$ $4 x^{2} + k x + 9$ a perfect square trinomial.
Find the two integer values of k that make $16 y^{2} + k y + 25$ $16 y^{2} + k y + 25$ a perfect square trinomial.
Find six values of k such that $x^{2} + k x + 18$ $x^{2} + k x + 18$ can be factored.
Explain why most students would find $24 x^{2} - 23 x - 12$ $24 x^{2} - 23 x - 12$ more difficult to factor than $23 x^{2} - 18 x - 5.$ $23 x^{2} - 18 x - 5.$

When an object is thrown upward with an initial velocity of

v_{0}

$v_{0}$ (in ft/s) from an initial height of

s_{0}

$s_{0}$ (in ft), its height after t seconds is given by

- 16 t^{2} + v_{0} t + s_{0}

$- 16 t^{2} + v_{0} t + s_{0}$ . In Exercises 71 and 72, find an expression for the height and write it in factored form.

$v_{0} = 32 ft / s, s_{0} = 128 ft$ $v_{0} = 32 ft / s, s_{0} = 128 ft$
$v_{0} = 24 ft / s, s_{0} = 40 ft$ $v_{0} = 24 ft / s, s_{0} = 40 ft$

Answers to Practice Exercises

$(x - 2) (x + 1)$ $(x - 2) (x + 1)$
$(x - 6) (x + 2)$ $(x - 6) (x + 2)$
$(6 s - 5 t) (s + 4 t)$ $(6 s - 5 t) (s + 4 t)$
$(3 x - 8) (x + 2)$ $(3 x - 8) (x + 2)$
${(3 x + 4)}^{2}$ ${(3 x + 4)}^{2}$
$3 (2 x - 1) (x + 2)$ $3 (2 x - 1) (x + 2)$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 6.2 Factoring Trinomials

Create new playlist

Sign In

Sign Up

Table of Contents for
6.2 Factoring Trinomials