19.4 The Binomial Theorem
Properties of • Factorial Notation • Binomial Theorem • Pascal’s Triangle • Binomial Series
To expand would require a number of multiplications that would be a tedious operation. We now develop the binomial theorem, by which it is possible to expand binomials to any given power without direct multiplication. Using this type of expansion, it is also possible to expand some expressions for which direct multiplication is not possible. The binomial theorem is used to develop expressions needed in certain mathematics topics and in technical applications.
By direct multiplication, we may obtain the following expansions of the binomial
Inspection shows these expansions have certain properties, and we assume that these properties are valid for the expansion of where n is any positive integer.
The following example illustrates the use of the basic properties in expanding a binomial. Carefully note the diagram in which each of these five properties is specifically noted.
EXAMPLE 1 Using basic binomial properties
Using the basic properties, develop the expansion for
Because the exponent of the binomial is 5, we have
From property 1, we know that there are six terms.
From property 2, we know that the first term is and the final term is
From property 3, we know that the factors of a and b in terms 2, 3, 4, and 5 are and respectively.
From property 4, we obtain the coefficients of terms 2, 3, 4, and 5. In the first term, the coefficient is 1. Multiplying by 5, the power of a, and dividing by 1, the number of the term, we obtain 5, which is the coefficient of the second term. Thus, the second term is Again using property 4, we obtain the coefficient of the third term. The coefficient of the second term is 5. Multiplying by 4, and dividing by 2, we obtain 10. This means that the third term is
From property 5, we know that the coefficient of the fifth term is the same as the second and that the coefficient of the fourth term is the same as the third. These properties are illustrated in the following diagram:

It is not necessary to use the above properties directly to expand a given binomial. If they are applied to a general formula for the expansion of a binomial may be obtained. In developing and stating the general formula, it is convenient to use the factorial notation n!, where
We see that n!, read “n factorial,” represents the product of the first n positive integers.
EXAMPLE 2 Evaluating factorials
In evaluating factorials, we must remember that they represent products of numbers.
CAUTION
In parts (d) and (e), we see that is not and 4!/2! is not 2!.
The evaluation of the factorials in Example 2 are shown in the calculator display in Fig. 19.10.

Fig. 19.10
Graphing calculator keystrokes: bit.ly/
THE BINOMIAL FORMULA
Based on the binomial properties, the binomial theorem states that the following binomial formula is valid for all positive integer values of n (the binomial theorem is proven through advanced methods).
EXAMPLE 3 Using the binomial formula
Using the binomial formula, expand
In using the binomial formula for we use 2x for a, 3 for b, and 6 for n.
Thus,
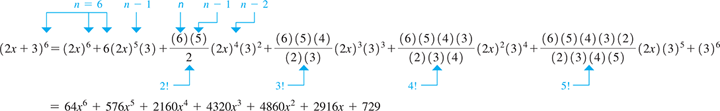
PASCAL’S TRIANGLE
For the first few integer powers of a binomial the coefficients can be obtained by setting them up in the following pattern, known as Pascal’s triangle.

We note that the first and last coefficients shown in each row are 1, and the second and next-to-last coefficients are equal to n. Other coefficients are obtained by adding the two nearest coefficients in the row above, as illustrated in Fig. 19.11 for the indicated section of Pascal’s triangle. This pattern may be continued indefinitely, although use of Pascal’s triangle is cumbersome for high values of n.
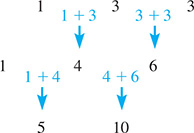
Fig. 19.11
EXAMPLE 4 Using Pascal‘s triangle
Using Pascal’s triangle, expand
Here, we note that Thus, the coefficients of the five terms are 1, 4, 6, 4, and 1, respectively. Also, here we use 5s for a and for b. We are expanding this expression as Therefore,

The coefficients 1, 4, 6, 4, and 1 are called binomial coefficients. In addition to using Pascal’s triangle, these coefficients can be found on a calculator as shown in Fig. 19.12.

Fig. 19.12
Graphing calculator keystrokes: bit.ly/
In certain uses of a binomial expansion, it is not necessary to obtain all terms. Only the first few terms are required. The following example illustrates finding the first four terms of an expansion.
EXAMPLE 5 Using the binomial formula
Find the first four terms of the expansion of
Here, we use x for a, 7 for b, and 12 for n. Thus, from the binomial formula, we have
If we let and in the binomial formula, we obtain the binomial series.
Through advanced methods, the binomial series can be shown to be valid for any real number n if When n is either negative or a fraction, we obtain an infinite series. In such a case, we calculate as many terms as may be needed although such a series is not obtainable through direct multiplication. The binomial series may be used to develop important expressions that are used in applications and more advanced mathematics topics.
EXAMPLE 6 Binomial series—forces on a beam
In the analysis of forces on beams, the expression is used. Use the binomial series to find the first four terms of the expansion.
Using negative exponents, we have
Now, in using Eq. (19.10), we have and
Therefore,
EXAMPLE 7 Evaluation using binomial series
Approximate the value of by use of the binomial series.
We note that which means Using four terms of the binomial series, we have
From a calculator, we find that (to six decimal places), which means these values agree to four significant digits with a value 0.8080. Greater accuracy can be found using the binomial series if more terms are used.
EXERCISES 19.4
In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the given problems.
In Exercises 3–12, expand and simplify the given expressions by use of the binomial formula.
In Exercises 13–16, expand and simplify the given expressions by use of Pascal’s triangle.
In Exercises 17–24, find the first four terms of the indicated expansions.
In Exercises 25–28, approximate the value of the given expression to three decimal places by using three terms of the appropriate binomial series. Check using a calculator.
In Exercises 29–36, find the first four terms of the indicated expansions by use of the binomial series.
In Exercises 37–40, solve the given problems involving factorials.
Using a calculator, evaluate (a) (b) 21!, (c) and (d) 68!.
Using a calculator, evaluate (a) (b) 8!/7!, (c) , and (d) 56!.
 Show that for To use this equation for explain why it is necessary to define (this is a standard definition of 0!).
Show that for To use this equation for explain why it is necessary to define (this is a standard definition of 0!).Show that for See Exercise 39.
In Exercises 41–44, find the indicated terms by use of the following information. The term of the expansion of is given by
The term involving in
The term involving in
The fifth term of
The sixth term of
In Exercises 45–58, solve the given problems.
Without expanding, evaluate
Add up the coefficients of the first few powers of by using Pascal’s triangle. Then by noting the pattern, determine the sum of the coefficients of
 Explain why n! ends in a zero if
Explain why n! ends in a zero if Expand using the binomial theorem. Group terms as indicated.
A mechanical system has 4 redundant engines, each with a 95% probability of functioning properly. When the binomial theorem is used to expand the resulting terms give the probabilities of exactly 4, 3, 2, 1, and 0 engines functioning properly. Find the probability of exactly 3 engines functioning properly (the term containing ). Round to the third decimal place.
In Exercise 49, find the probability that at least one engine functions properly (the sum of the terms containing and ). Round to the third decimal place.
Approximate to hundredths by noting that and using four terms of the appropriate binomial series.
Approximate by using the method of Exercise 51.
A company purchases a piece of equipment for A dollars, and the equipment depreciates at a rate of r each year. Its value V after n years is Expand this expression for
In finding the rate of change of emission of energy from the surface of a body at temperature T, the expression is used. Expand this expression.
In the theory associated with the magnetic field due to an electric current, the expression is found. By expanding find the first three nonzero terms that could be used to approximate the given expression.
In the theory related to the dispersion of light, the expression arises. (a) Let and find the first four terms of the expansion of (b) Find the same expansion by using long division. (c) Write the original expression in expanded form, using the results of (a) and (b).
A cubic Bezier curve is defined by four points ( through ) from the parametric equations given by where Note that the points through are multiplied by terms of the binomial expansion Using a similar process, find the equation of the fourth-degree Bezier curve defined by the five points through (see Example 6 in Section 15.3).
Find the first four terms of the expansion of and then divide into 1. Compare the results.
Answers to Practice Exercises
72
1.230 (rounded off)
