8.2 Trigonometric Functions of Any Angle
Reference Angle • Evaluating Trigonometric Functions • Evaluations on a Calculator • Quadrantal Angles • Negative Angles
In the last section, we saw that the signs of the trigonometric functions depend on the quadrant of In this section, we will investigate an important connection between certain angles in different quadrants. To illustrate this, let’s start by taking the sine of the angles , , , and . These values are shown in Fig. 8.5.

Fig. 8.5
The signs of the function values agree with what we would expect; is positive in quadrants I and II and negative in quadrants III and IV. The important thing to notice, however, is that the numerical values (disregarding the signs) are the same for all four angles. The reason for this is that these angles have something in common, called a reference angle, which is defined below:
In our example, all four angles have a reference angle of . Figure 8.6 shows the terminal sides of these angles drawn in standard position along with their reference angles. Since the angles share a common reference angle, they will also have the same trigonometric function values, neglecting the sign. Our example demonstrated this for sine, and the same is true for the other five functions. This is because the values of x, y, and r in the definition of the trigonometric functions will be the same, except for the signs of x and y, which will depend on the quadrant.

Fig. 8.6
For this reason, reference angles are very important in trigonometry. To find the reference angle of a given angle, we sketch the angle in standard position and then determine the acute angle between its terminal side and the x-axis. This is illustrated in the following example.
EXAMPLE 1 Finding reference angles
Figure 8.7 shows the reference angles of , , , and . Pay careful attention to how the reference angle is calculated in each of the four quadrants.
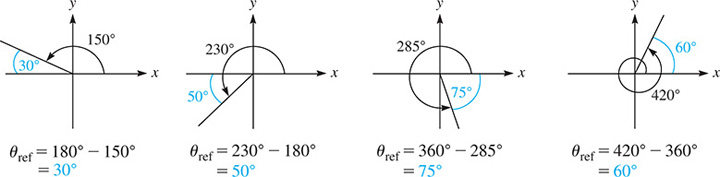
Fig. 8.7
We have observed that the trigonometric functions of different angles with the same reference angle will be the same, except for possibly the sign. Since the reference angle is an acute angle, it will always have a positive function value. The signs in the other quadrants will follow the rules stated in Section 8.1. This is summarized below:
According to the statement above, etc. This means that a trigonometric function of any angle can be found by first finding the trigonometric function of its reference angle and then attaching the correct sign, depending on the quadrant. The following example illustrates this process.
EXAMPLE 2 Evaluating using reference angles
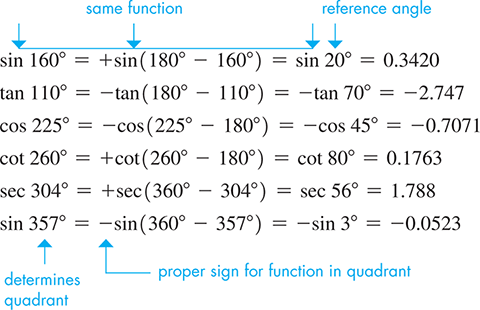
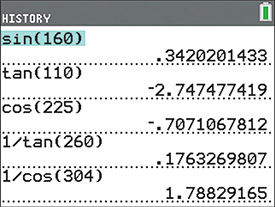
Fig. 8.8
A calculator will give values, with the proper signs, of functions like those in Example 2. To find and we must take the reciprocal of the corresponding function. For example, The display for the first five lines of Example 2 is shown in Fig. 8.8.
NOTE
[In most examples, we will round off values to four significant digits (as in Example 2). However, if the angle is approximate, use the guidelines in Table 4.1 of Section 4.3 for rounding off values.]
EXAMPLE 3 Quadrant II angle—area of triangle
A formula for finding the area of a triangle, knowing sides a and b and the included is A surveyor uses this formula to find the area of a triangular tract of land for which and See Fig. 8.9.
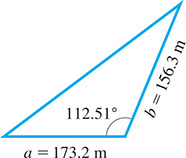
Fig. 8.9
The calculator automatically uses a positive value for .
Reference angles are especially important when we wish to find an angle that has a given trigonometric function value. This is because the inverse trigonometric functions on a calculator are programmed to give angles within the specific intervals shown below:
always returns an angle between and
always returns an angle between and
always returns and angle between and
CAUTION
Sometimes we wish to find an angle that is not within the intervals given above. This is when reference angles must be used.
For example, if we need to find a second quadrant angle for which , then taking will not return the correct angle. In this type of situation, we must use the reference angle to find the correct angle. This is illustrated in the following examples.
EXAMPLE 4 Finding angles given sinθ
If we see from the first line of the calculator display shown in Fig. 8.10 that (rounded off).

Fig. 8.10
This result is correct, but remember that there is also a second quadrant angle (where sine is also positive) that has a sine of 0.2550. This angle has a reference angle of and is therefore given by .
If we need only an acute angle, is correct. However, if a second-quadrant angle is required, we see that is the angle (see Fig. 8.11). These can be checked by finding the values of and .
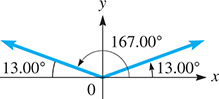
Fig. 8.11
EXAMPLE 5 Finding angles given secθ
For and (this means may equal or be between and ), we see from the second line of the calculator display shown in Fig. 8.10 that (rounded off).
The angle is the second-quadrant angle, but in the third quadrant as well. The reference angle is and the third-quadrant angle is Therefore, the two angles between and for which are and (see Fig. 8.12). These angles can be checked by finding and .

Fig. 8.12
EXAMPLE 6 Finding angles given tan θ
Given that and find for
Because is positive and is negative, must be a third-quadrant angle. A calculator will display an angle of (rounded off) for However, because we need a third-quadrant angle, we must add (the reference angle) to . Thus, the required angle is (see Fig. 8.13). Check by finding .

Fig. 8.13
If and the calculator will display an angle of for We would then have to recognize that the reference angle is and subtract it from to get , the required second-quadrant angle. This can be checked by finding .
The calculator gives the reference angle (disregarding any minus signs) in all cases except when is negative. Then it can be used to determine the angle required by the problem.
NOTE
[To avoid confusion from the angle displayed by the calculator, a good procedure is to find the reference angle first.]
We can find the reference angle by entering the absolute value of the function. The displayed angle will be the reference angle. The required angle is then found by using the reference angle along with the quadrant of as shown below:
EXAMPLE 7 Using reference angle
Given that find for
Because is negative, is either a second-quadrant angle or a third-quadrant angle. Using 0.1298, the calculator tells us that the reference angle is .
For the second-quadrant angle, we subtract from to get . For the third-quadrant angle, we add to to get . See Fig. 8.14. Therefore, the two solutions are and .
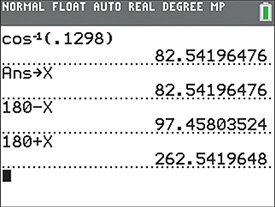
Fig. 8.14
In Section 4.2, we showed how the unit circle could be used to evaluate the trigonometric functions. We now restate this as a definition, which is a special case of the general definition in Eq. (8.1) with the restriction that
There are many situations when the unit circle definition is useful, including evaluating trigonometric functions of quadrantal angles, which have their terminal side along one of the axes (see Fig. 8.16). The sine of is simply the y-coordinate on the unit circle, and the cosine of is the x-coordinate. The other functions are found by taking ratios, and if the denominator is zero, the function is undefined.

Fig. 8.16
EXAMPLE 8 Quadrantal angles and the unit circle
Find the six trigonometric functions of .
As shown in Fig. 8.16(a), intersects the unit circle at (1, 0). Therefore,
Find the six trigonometric functions of .
As shown in Fig. 8.16(d), intersects the unit circle at Thus,
To evaluate functions of negative angles, we can use functions of corresponding positive angles, if we use the correct sign. In Fig. 8.17, note that and which means In the same way, we can get all of the relations between functions of and the functions of Therefore,

Fig. 8.17
EXAMPLE 9 Negative angles
EXERCISES 8.2
In Example 2, add to each angle, express in terms of the same function of a positive acute angle, and then evaluate.
In Example 7, change the to and then find
,
,
,
,
Find when and
Find when and
Find when and
Find when and
Using the fact that evaluate .
Using the fact that evaluate .
Express in terms of the
Express in terms of
For a triangle with angles A, B, and C, evaluate
(a) Is (b) Is
The current i in an alternating-current circuit is given by where is the maximum current in the circuit. Find i if and
The force F that a rope exerts on a crate is related to force directed along the x-axis by where is the standard-position angle for F. See Fig. 8.18. Find F if and
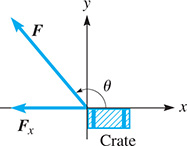
Fig. 8.18
For the slider mechanism shown in Fig. 8.19, Find y if in., and
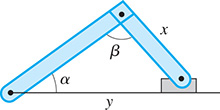
Fig. 8.19
A laser follows the path shown in Fig. 8.20. The angle is related to the distances a, b, and c by Find if and

Fig. 8.20
Answers to Practice Exercises
,
undefined
