4.2 Defining the Trigonometric Functions
Definitions of the Trigonometric Functions • Evaluating the Trigonometric Functions • The Unit Circle
In this section, we define the six trigonometric functions. These functions are used in a wide variety of technological fields to solve problems involving triangles as well as quantities that oscillate repeatedly. The six trigonometric functions are defined below.
DEFINITION OF THE TRIGONOMETRIC FUNCTIONS
Let (x, y) be any point (other than the origin) on the terminal side of the angle in standard position, and let r be the distance between the origin and the given point (see Fig. 4.10).
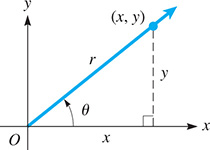
Fig. 4.10
Then the six trigonometric functions are defined as follows:
NOTE
[It is important to notice the reciprocal relationships that exist between sine and cosecant, cosine and secant, and tangent and cotangent.]
If we know the value of one of the trigonometric functions, then we can find the value of the corresponding reciprocal function by interchanging the numerator and denominator.
The definition given above is completely general, which means it applies to all angles, no matter which of the four quadrants they terminate in. However, in this chapter, we will concentrate on angles between and . In Chapters 8 and 20, we will expand our scope and apply this definition to angles terminating in all four quadrants. In all cases, the distance r from the origin to the point is always a positive number, and it is called the radius vector. This will affect the domains of those functions, which will be discussed in Chapter 10 when we investigate their graphs.
NOTE
[It should also be noted that when either or some of the trigonometric ratios are undefined because their denominator is zero.]
EXAMPLE 1 Trigonometric ratios are independent of point
The definition of the trigonometric functions allows us to use any point on the terminal side of to determine the six trigonometric ratios. [It is important to realize that no matter which point we decide to use, we will get the same answer for these ratios].
For example, using point P in Fig. 4.11, we get If we use point Q, we get Since the triangles ORP and OSQ are similar triangles (their corresponding angles are equal), their corresponding sides must be proportional (see Section 2.2). This means or equivalently, by multiplying both sides by

Fig. 4.11
This proves that meaning that we will arrive at the same answer for no matter which point we use on the terminal side. The same can be shown for the other trigonometric ratios. Therefore, each trigonometric ratio depends solely on the angle and for each value of there will be only one value of each trigonometric ratio. This means that the ratios are functions of the angle and this is why we call them trigonometric functions.
EVALUATING THE TRIGONOMETRIC FUNCTIONS
The definitions in Eqs. (4.1) are used in evaluating the trigonometric functions. Also, we often use the Pythagorean theorem, which is discussed in Section 2.2, and which we restate here for reference. For the right triangle in Fig. 4.12, with hypotenuse c and legs a and b,
Therefore, in Fig. 4.10 on the previous page, or
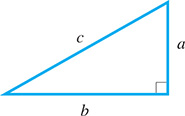
Fig. 4.12
EXAMPLE 2 Values of trigonometric functions
Find the values of the trigonometric functions of the standard-position angle with its terminal side passing through the point (3, 4).
By placing the angle in standard position, as shown in Fig. 4.13, and drawing the terminal side through (3, 4), we find by use of the Pythagorean theorem that
Using the values and we find that
We have left each of these results in the form of a fraction, which is considered to be an exact form in that there has been no approximation made. In writing decimal values, we find that and where these values have been rounded off and are therefore approximate.
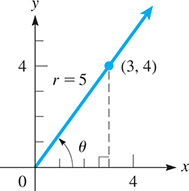
Fig. 4.13
EXAMPLE 3 Values of trigonometric functions
Find the values of the trigonometric functions of the standard-position angle whose terminal side passes through (7.27, 4.19). The coordinates are approximate.
We show the angle and the given point in Fig. 4.14. From the Pythagorean theorem, we have
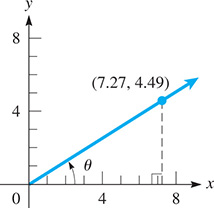
Fig. 4.14
(Here, we show a rounded-off value of r. It is not actually necessary to record the value of r because its value can be stored in the memory of a calculator. The reason for recording it here is to show the values used in the calculation of each of the trigonometric functions.) Therefore, we have the following values:
Because the coordinates are approximate, the results are rounded off.
The trigonometric functions can be evaluated directly on a calculator without rounding intermediate steps by storing the value of r and then using this stored value to compute the trigonometric ratios. The calculator evaluations of and are shown in Fig. 4.15.

Fig. 4.15
CAUTION
In Example 3, we expressed the result as A common error is to omit the angle and give the value as This is a meaningless expression, for we must show the angle for which we have the value of a function.
If one of the trigonometric functions is known, it is possible to find the values of the other functions. The following example illustrates the method.
EXAMPLE 4 Given one function—find others
If we know that and that is a first-quadrant angle, we know the ratio of the ordinate to the radius vector (y to r) is 3 to 7. Therefore, the point on the terminal side for which can be found by use of the Pythagorean theorem:
Therefore, the point is on the terminal side, as shown in Fig. 4.16.
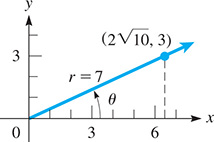
Fig. 4.16
Using the values and we have the other trigonometric functions of They are
These values are exact. Approximate decimal values found on a calculator are
THE UNIT CIRCLE AND THE TRIGONOMETRIC FUNCTIONS
The circle that is centered at the origin and has a radius of 1 is called the unit circle. Suppose the terminal side of in standard position intersects the unit circle at the point (x, y) as shown is Fig. 4.17.
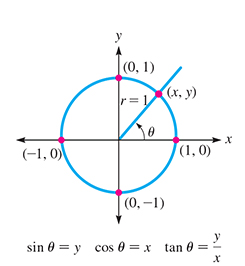
Fig. 4.17
Using the definition of the trigonometric functions and the fact that and Thus, the y-coordinate of the point on the unit circle equals and the x-coordinate equals This fact can be very useful in many situations.
In terms of the unit circle, the same as in the original definition. Also, the three reciprocal functions are still found by taking the reciprocal of the sine, cosine, or tangent.
EXAMPLE 5 The unit circle
Use the unit circle to find and .
A angle, when placed in standard position, intersects the unit circle at the point (0,1). Therefore, and
Find and if the terminal side of (in standard position) intersects the unit circle at the point (0.6, 0.8).
We know that . Since is the reciprocal of 0.8.
Thus,
EXERCISES 4.2
In Exercises 1 and 2, answer the given questions about the indicated examples of this section.
In Example 2, if (4, 3) replaces (3, 4), what are the values?
In Example 4, if 4/7 replaces 3/7, what are the values?
In Exercises 3–18, find values of the trigonometric functions of the angle (in standard position) whose terminal side passes through the given points. For Exercises 3–16, give answers in exact form. For Exercises 17 and 18, the coordinates are approximate.
(6, 8)
(5, 12)
(15, 8)
(240, 70)
(0.09, 0.40)
(1.1, 6.0)
(1.2, 3.5)
(1.2, 0.9)
(7, 7)
(840, 130)
(50, 20)
(0.687, 0.943)
(37.65, 21.87)
In Exercises 19–26, find the values of the indicated functions. In Exercises 19–22, give answers in exact form. In Exercises 23–26, the values are approximate.
Given find and
Given find and
Given find and
Given find and
Given find and
Given find and
Given find and
Given find and
In Exercises 27–30, each given point is on the terminal side of an angle. Show that each of the given functions is the same for each point.
(3, 4), (6, 8), (4.5, 6), and
(5, 12), (15, 36), (7.5, 18), and
(0.3, 0.1), (9, 3), (33, 11), and
(40, 30), (56, 42), (36, 27), and
Use the unit circle to complete Exercises 31–34 (see Example 5).
Find
Find
If the intersects the unit circle at exactly (0.28, 0.96), find and
For the angle in Exercise 33, find and
In Exercises 35–42, answer the given questions.
For an acute angle A, which is greater, sin A or tan A?
For an acute angle which is less, tan A or cot A?
If what is the value of
If what is the value of
If what is in terms of y?
If what is in terms of x?
From the definitions of the trigonometric functions, it can be seen that is the reciprocal of What function is the reciprocal of
 Refer to the definitions of the trigonometric functions in Eqs. (4.1). Is the quotient of one of the functions divided by equal to Explain.
Refer to the definitions of the trigonometric functions in Eqs. (4.1). Is the quotient of one of the functions divided by equal to Explain.
