Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

14.3 Equations in Quadratic Form

Substituting to Fit Quadratic Form • Solving Equations in Quadratic Form • Extraneous Roots

Often, we encounter equations that can be solved by methods applicable to quadratic equations, even though these equations are not actually quadratic.

NOTE

[They do have the property, however, that with a proper substitution they may be written in the form of a quadratic equation.]

All that is necessary is that the equation have terms including some variable quantity, its square, and perhaps a constant term. The following example illustrates these types of equations.

EXAMPLE 1 Identifying quadratic form

The equation $x - 2 \sqrt{x} - 5 = 0$ $x - 2 \sqrt{x} - 5 = 0$ is an equation in quadratic form, because if we let $y = \sqrt{x},$ $y = \sqrt{x},$ we have $x = {(\sqrt{x})}^{2} = y^{2},$ $x = {(\sqrt{x})}^{2} = y^{2},$ and the resulting equation is $y^{2} - 2 y - 5 = 0.$ $y^{2} - 2 y - 5 = 0.$
$t^{- 4} - 5 t^{- 2} + 3 = 0$ $t^{- 4} - 5 t^{- 2} + 3 = 0$
$t^{3} - 3 t^{3/2} - 7 = 0$ $t^{3} - 3 t^{3/2} - 7 = 0$
${(x + 1)}^{4} - {(x + 1)}^{2} - 1 = 0$ ${(x + 1)}^{4} - {(x + 1)}^{2} - 1 = 0$
$x^{10} - 2 x^{5} + 1 = 0$ $x^{10} - 2 x^{5} + 1 = 0$

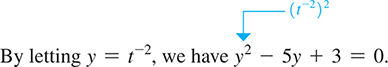
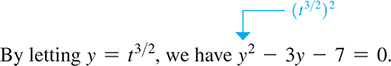
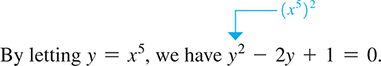
The following examples illustrate the method of solving equations in quadratic form.

EXAMPLE 2 Solving an equation in quadratic form

Solve the equation $2 x^{4} + 7 x^{2} = 4.$ $2 x^{4} + 7 x^{2} = 4.$

We first let $y = x^{2}$ $y = x^{2}$ to write the equation in quadratic form. We will then solve the resulting quadratic equation for y. However, solutions for x are required, so we again let $y = x^{2}$ $y = x^{2}$ to solve for x.

\begin{array}{rcl} 2 y^{2} + 7 y - 4 & = & 0 & let y = x^{2} \\ (2 y - 1) (y + 4) & = & 0 & factor and solve for y \\ y = \frac{1}{2} or y & = & - 4 \\ x^{2} = \frac{1}{2} or x^{2} & = & - 4 & y = x^{2} (to solve for x) \\ x = \pm \frac{1}{\sqrt{2}} or x & = & \pm 2 j \end{array}

$\begin{array}{rcl} 2 y^{2} + 7 y - 4 & = & 0 & let y = x^{2} \\ (2 y - 1) (y + 4) & = & 0 & factor and solve for y \\ y = \frac{1}{2} or y & = & - 4 \\ x^{2} = \frac{1}{2} or x^{2} & = & - 4 & y = x^{2} (to solve for x) \\ x = \pm \frac{1}{\sqrt{2}} or x & = & \pm 2 j \end{array}$

We can let $y_{1} = 2 x^{4} + 7 x^{2}$ $y_{1} = 2 x^{4} + 7 x^{2}$ and $y_{2} = 4$ $y_{2} = 4$ to solve the system on a calculator. The display is shown in Fig. 14.15, and we see that there are two points of intersection, one for $x = 0.7071$ $x = 0.7071$ (shown on screen) and the other for $x = - 0.7071$ $x = - 0.7071$ (not shown). Because $1 / \sqrt{2} = 0.7071,$ $1 / \sqrt{2} = 0.7071,$ this verifies the real solutions. The imaginary solutions cannot be found graphically. Substitution of each value in the original equation shows each value to be a solution.

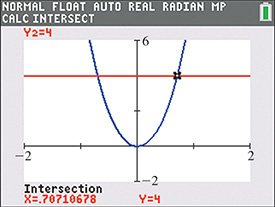
A parabola opens upward with vertex (0, 0). The horizontal line y sub 2 = 4 intersects the parabola at (0.70710678, 4). — Fig. 14.15
Graphing calculator keystrokes: bit.ly/2Eidip7

Two of the solutions in Example 2 are complex numbers. We were able to find these solutions directly from the definition of the square root of a negative number. In some cases (see Exercise 22 of this section), it is necessary to use the method of Section 12.6 to find such complex-number solutions.

EXAMPLE 3 Solving an equation with a square root

Solve the equation $x - \sqrt{x} - 2 = 0.$ $x - \sqrt{x} - 2 = 0.$

By letting $y = \sqrt{x},$ $y = \sqrt{x},$ we have

\begin{array}{l} \begin{array}{rcl} y^{2} - y - 2 & = & 0 \\ (y - 2) (y + 1) & = & 0 \\ y = 2 or y & = & - 1 \end{array} \\ \begin{array}{rclcl} \sqrt{x} & = & 2 & or & \sqrt{x} = - 1 & y = \sqrt{x} \\ x & = & 4 & no soultion \end{array} \end{array}

$\begin{array}{l} \begin{array}{rcl} y^{2} - y - 2 & = & 0 \\ (y - 2) (y + 1) & = & 0 \\ y = 2 or y & = & - 1 \end{array} \\ \begin{array}{rclcl} \sqrt{x} & = & 2 & or & \sqrt{x} = - 1 & y = \sqrt{x} \\ x & = & 4 & no soultion \end{array} \end{array}$

Since $\sqrt{x}$ $\sqrt{x}$ cannot be negative, the only solution is $x = 4.$ $x = 4.$ This solution checks when substituted in the original equation.

The graph of $y_{1} = x - \sqrt{x} - 2$ $y_{1} = x - \sqrt{x} - 2$ is shown in the calculator display in Fig. 14.16. Note that $x = 4$ $x = 4$ is the only solution shown.

The curve y sub 1 = x minus square root of, x, minus 2, rises from approximately (0, 2) and through a zero at (4, 0). — Fig. 14.16
Graphing calculator keystrokes: bit.ly/2OV0mcR

CAUTION

Example 3 illustrates a very important point. Whenever an operation involving the unknown is performed on an equation, this operation may introduce roots into a subsequent equation that are not roots of the original equation. Therefore, we must check all answers in the original equation.

Only operations involving constants—that is, adding, subtracting, multiplying by, or dividing by constants—are certain not to introduce the extraneous roots. We first encountered the concept of an extraneous root in Section 6.7, when we discussed equations involving fractions.

EXAMPLE 4 Solving an equation with negative exponents

Solve the equation $x^{- 2} + 3 x^{- 1} + 1 = 0.$ $x^{- 2} + 3 x^{- 1} + 1 = 0.$

By substituting $y = x^{- 1},$ $y = x^{- 1},$ we have $y^{2} + 3 y + 1 = 0.$ $y^{2} + 3 y + 1 = 0.$ To solve this equation, we may use the quadratic formula:

y = \frac{- 3 \pm \sqrt{9 - 4}}{2} = \frac{- 3 \pm \sqrt{5}}{2}

$y = \frac{- 3 \pm \sqrt{9 - 4}}{2} = \frac{- 3 \pm \sqrt{5}}{2}$

Since $x = 1 / y,$ $x = 1 / y,$ we have

\begin{array}{l} x = \frac{2}{- 3 + \sqrt{5}} & or & x = \frac{2}{- 3 - \sqrt{5}} \end{array}

$\begin{array}{l} x = \frac{2}{- 3 + \sqrt{5}} & or & x = \frac{2}{- 3 - \sqrt{5}} \end{array}$

These answers in decimal form are

\begin{array}{l} x \approx - 2.618 & or & x \approx - 0.382 \end{array}

$\begin{array}{l} x \approx - 2.618 & or & x \approx - 0.382 \end{array}$

These results check when substituted in the original equation. In checking these decimal answers, it is more accurate to use the calculator values, before rounding them off. This can be done by storing the calculator values in memory.

EXAMPLE 5 Solving an equation with grouped terms

Solve the equation ${(x^{2} - x)}^{2} - 8 (x^{2} - x) + 12 = 0.$ ${(x^{2} - x)}^{2} - 8 (x^{2} - x) + 12 = 0.$

By substituting $y = x^{2} - x,$ $y = x^{2} - x,$ we have

\begin{array}{l} \begin{array}{rcl} y^{2} - 8 y + 12 & = & 0 \\ (y - 2) (y - 6) & = & 0 \\ y = 2 or y & = & 6 \end{array} \\ \begin{array}{l} x^{2} - x = 2 & or & x^{2} - x = 6 & y = x^{2} - x \end{array} \end{array}

$\begin{array}{l} \begin{array}{rcl} y^{2} - 8 y + 12 & = & 0 \\ (y - 2) (y - 6) & = & 0 \\ y = 2 or y & = & 6 \end{array} \\ \begin{array}{l} x^{2} - x = 2 & or & x^{2} - x = 6 & y = x^{2} - x \end{array} \end{array}$

Solving each of these equations, we have

\begin{array}{rclrcl} x^{2} - x - 2 & = & 0 & x^{2} - x - 6 & = & 0 \\ (x - 2) (x + 1) & = & 0 & (x - 3) (x + 2) & = & 0 \\ x = 2 or x & = & - 1 & x = 3 or x & = & - 2 \end{array}

$\begin{array}{rclrcl} x^{2} - x - 2 & = & 0 & x^{2} - x - 6 & = & 0 \\ (x - 2) (x + 1) & = & 0 & (x - 3) (x + 2) & = & 0 \\ x = 2 or x & = & - 1 & x = 3 or x & = & - 2 \end{array}$

Each value checks when substituted in the original equation.

EXAMPLE 6 Quadratic form—cell phone screen

An advertisement for a cell phone states that it has a 106-mm screen (diagonal) with an area of ${5040 mm}^{2} .$ ${5040 mm}^{2} .$ Find the length l and width w of the screen. See Fig. 14.17.

A phone screen with length l, width w, diagonal 106 millimeters, and area Ay = 5040 millimeters squared. — Fig. 14.17

Because the required quantities are the length and width, let $l = the$ $l = the$ length of the screen and let $w = its$ $w = its$ width. Because the area is ${5040 mm}^{2}, l w = 5040.$ ${5040 mm}^{2}, l w = 5040.$ Also, using the Pythagorean theorem and the fact that the diagonal is 106 mm, we have the equation $l^{2} + w^{2} = 106^{2} .$ $l^{2} + w^{2} = 106^{2} .$ Therefore, we are to solve the system of equations

l w = 5040 l^{2} + w^{2} = 11, 236

$l w = 5040 l^{2} + w^{2} = 11, 236$

Solving the first equation for l, we have $l = 5040 / w .$ $l = 5040 / w .$ Substituting this into the second equation, we have

\begin{array}{rcl} {(\frac{5040}{w})}^{2} + w^{2} & = & 11, 236 \\ \frac{5040^{2}}{w^{2}} + w^{2} & = & 11, 236 \\ 25, 401, 600 + w^{4} & = & 11, 236 w^{2} \end{array}

$\begin{array}{rcl} {(\frac{5040}{w})}^{2} + w^{2} & = & 11, 236 \\ \frac{5040^{2}}{w^{2}} + w^{2} & = & 11, 236 \\ 25, 401, 600 + w^{4} & = & 11, 236 w^{2} \end{array}$

Let $x = w^{2},$ $x = w^{2},$

\begin{array}{l} x^{2} - 11, 236 x + 25, 401, 600 = 0 \\ \begin{array}{rcl} x & = & \frac{- (- 11, 236) \pm \sqrt{{(- 11, 236)}^{2} - 4 (1) (25, 401, 600)}}{2 (1)} \\ x & = & 8100 or x = 3136 \end{array} \end{array}

$\begin{array}{l} x^{2} - 11, 236 x + 25, 401, 600 = 0 \\ \begin{array}{rcl} x & = & \frac{- (- 11, 236) \pm \sqrt{{(- 11, 236)}^{2} - 4 (1) (25, 401, 600)}}{2 (1)} \\ x & = & 8100 or x = 3136 \end{array} \end{array}$

Therefore, $w^{2} = 8100,$ $w^{2} = 8100,$ or $w^{2} = 3136.$ $w^{2} = 3136.$

Solving for w, we get $w = \pm 90,$ $w = \pm 90,$ or $w = \pm 56.$ $w = \pm 56.$ Only positive values are meaningful in this problem, which means if $w = 56 mm,$ $w = 56 mm,$ then $l = 90 mm$ $l = 90 mm$ (or $l = 56 mm, w = 90 mm$ $l = 56 mm, w = 90 mm$ ). Checking with the statement of the problem, we see that these dimensions for the screen give an area of ${5040 mm}^{2}$ ${5040 mm}^{2}$ and a diagonal of 106 mm.

EXERCISES 14.3

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting equations

In Example 2, change the $+$ $+$ before the $7 x^{2}$ $7 x^{2}$ to $-$ $-$ and then solve the equation.
In Example 3, change the 2 to 6 and then solve the equation.

In Exercises 3–28, solve the given equations algebraically. In Exercise 10, explain your method

$x^{4} - 10 x^{2} + 9 = 0$ $x^{4} - 10 x^{2} + 9 = 0$
$4 R^{4} + 15 R^{2} = 4$ $4 R^{4} + 15 R^{2} = 4$
$3 x^{- 2} - 7 x^{- 1} - 6 = 0$ $3 x^{- 2} - 7 x^{- 1} - 6 = 0$
$10 x^{- 2} + 3 x^{- 1} - 1 = 0$ $10 x^{- 2} + 3 x^{- 1} - 1 = 0$
$x^{- 4} + 2 x^{- 2} = 24$ $x^{- 4} + 2 x^{- 2} = 24$
$x^{- 1} - x^{- 1/2} = 2$ $x^{- 1} - x^{- 1/2} = 2$
$2 x - 5 \sqrt{x} + 3 = 0$ $2 x - 5 \sqrt{x} + 3 = 0$
$4 x + 3 \sqrt{x} = 1$ $4 x + 3 \sqrt{x} = 1$
$3 \sqrt[3]{x} - 5 \sqrt[6]{x} + 2 = 0$ $3 \sqrt[3]{x} - 5 \sqrt[6]{x} + 2 = 0$
$\sqrt{x} + 3 \sqrt[4]{x} = 28$ $\sqrt{x} + 3 \sqrt[4]{x} = 28$
$x^{2/3} - 2 x^{1/3} - 15 = 0$ $x^{2/3} - 2 x^{1/3} - 15 = 0$
$y^{3} + 2 y^{3/2} = 80$ $y^{3} + 2 y^{3/2} = 80$
$8 n^{1/2} - 20 n^{1/4} = 12$ $8 n^{1/2} - 20 n^{1/4} = 12$
$3 x^{4/3} + 5 x^{2/3} = 2$ $3 x^{4/3} + 5 x^{2/3} = 2$
$(x - 1) - \sqrt{x - 1} = 20$ $(x - 1) - \sqrt{x - 1} = 20$
${(C + 1)}^{- 2/3} + 5 {(C + 1)}^{- 1/3} - 6 = 0$ ${(C + 1)}^{- 2/3} + 5 {(C + 1)}^{- 1/3} - 6 = 0$
${(x^{2} - 2 x)}^{2} - 11 (x^{2} - 2 x) + 24 = 0$ ${(x^{2} - 2 x)}^{2} - 11 (x^{2} - 2 x) + 24 = 0$
${(x^{2} - 1)}^{2} + {(x^{2} - 1)}^{- 2} = 2$ ${(x^{2} - 1)}^{2} + {(x^{2} - 1)}^{- 2} = 2$
$x - 3 \sqrt{x - 2} = 6 (Let y = \sqrt{x - 2} .)$ $x - 3 \sqrt{x - 2} = 6 (Let y = \sqrt{x - 2} .)$
$x^{6} + 7 x^{3} = 8$ $x^{6} + 7 x^{3} = 8$
$\frac{1}{{(x - 1)}^{2}} + \frac{1}{x - 1} = 12$ $\frac{1}{{(x - 1)}^{2}} + \frac{1}{x - 1} = 12$
$x^{2} - 3 x = \sqrt{x^{2} - 3 x} + 2$ $x^{2} - 3 x = \sqrt{x^{2} - 3 x} + 2$
$\frac{1}{s^{2} + 1} + \frac{2}{s^{2} + 3} = 1$ $\frac{1}{s^{2} + 1} + \frac{2}{s^{2} + 3} = 1$
${(x + \frac{2}{x})}^{2} - 6 x - \frac{12}{x} = - 9$ ${(x + \frac{2}{x})}^{2} - 6 x - \frac{12}{x} = - 9$
$e^{2 x} - 3 e^{x} + 2 = 0$ $e^{2 x} - 3 e^{x} + 2 = 0$
$10^{2 x} - 2 (10^{x}) = 0$ $10^{2 x} - 2 (10^{x}) = 0$

In Exercises 29–34, solve the given equations algebraically and check the solutions with a calculator

$x^{4} - 20 x^{2} + 64 = 0$ $x^{4} - 20 x^{2} + 64 = 0$
$x^{- 2} - x^{- 1} - 42 = 0$ $x^{- 2} - x^{- 1} - 42 = 0$
$x + 2 = 3 \sqrt{x}$ $x + 2 = 3 \sqrt{x}$
$3 x^{2/3} = 12 x^{1/3} + 36$ $3 x^{2/3} = 12 x^{1/3} + 36$
${(\log x)}^{2} - 3 \log x + 2 = 0$ ${(\log x)}^{2} - 3 \log x + 2 = 0$
$2^{x} + 32 (2^{- x}) = 12$ $2^{x} + 32 (2^{- x}) = 12$

In Exercises 35–42, solve the given problems algebraically.

Solve for $x : \log (x^{4} + 4) - \log (5 x^{2}) = 0.$ $x : \log (x^{4} + 4) - \log (5 x^{2}) = 0.$
A paper drinking cup in the shape of a cone is constructed from $6 π {in.}^{2}$ $6 π {in.}^{2}$ of paper. If the height of the cone is 4 in., find the radius. (Hint: Lateral surface area $S = π r \sqrt{r^{2} + h^{2}} .$ $S = π r \sqrt{r^{2} + h^{2}} .$ )
The equivalent resistance $R_{T}$ $R_{T}$ of two resistors $R_{1}$ $R_{1}$ and $R_{2}$ $R_{2}$ in parallel is given by $R_{T}^{- 1} = R_{1}^{- 1} + R_{2}^{- 1} .$ $R_{T}^{- 1} = R_{1}^{- 1} + R_{2}^{- 1} .$ If $R_{T} = 1.00 Ω$ $R_{T} = 1.00 Ω$ and $R_{2} = \sqrt{R_{1}},$ $R_{2} = \sqrt{R_{1}},$ find $R_{1}$ $R_{1}$ and $R_{2} .$ $R_{2} .$
An equation used in the study of the dispersion of light is $μ = A + B λ^{- 2} + C λ^{- 4} .$ $μ = A + B λ^{- 2} + C λ^{- 4} .$ Solve for $λ .$ $λ .$ (See the chapter introduction.)
In the theory dealing with optical interferometers, the equation $\sqrt{F} = 2 \sqrt{p} / (1 - p)$ $\sqrt{F} = 2 \sqrt{p} / (1 - p)$ is used. Solve for p if $F = 16.$ $F = 16.$
A special washer is made from a circular disc 3.50 cm in radius by removing a rectangular area of $12.0 {cm}^{2}$ $12.0 {cm}^{2}$ from the center. If each corner of the rectangular area is 0.50 cm from the outer edge of the washer, what are the dimensions of the area that is removed?
A rectangular TV screen has an area of $1540 in .^{2}$ $1540 in .^{2}$ and a diagonal of 60.0 in. Find the dimensions of the screen.
A roof truss in the shape of a right triangle has a perimeter of 90 ft. If the hypotenuse is 1 ft longer than one of the other sides, what are the sides of the truss?

Answers to Practice Exercises

1
$1/2, 1/2, - 1/2, - 1/2$ $1/2, 1/2, - 1/2, - 1/2$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 14.3 Equations in Quadratic Form

Create new playlist

Sign In

Sign Up

Table of Contents for
14.3 Equations in Quadratic Form