Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

21.7 Translation of Axes

Centers of Curves Not at Origin • Axes of Curves Parallel to Coordinate Axes • Translation of Axes

The equations we have considered for the parabola, the ellipse, and the hyperbola are those for which the center of the ellipse or hyperbola, or vertex of the parabola, is at the origin. In this section, we consider, without specific use of the definition, the equations of these curves for the cases in which the axis of the curve is parallel to one of the coordinate axes. This is done by translation of axes.

In Fig. 21.83, we choose a point (h, k) in the xy-coordinate plane as the origin of another coordinate system, the $x^{'} y^{'} - coordinate$ $x^{'} y^{'} - coordinate$ system. The $x^{'} - axis$ $x^{'} - axis$ is parallel to the x-axis and the $y^{'} - axis$ $y^{'} - axis$ is parallel to the y-axis. Every point now has two sets of coordinates (x, y) and $(x^{'}, y^{'}) .$ $(x^{'}, y^{'}) .$ We see that

Figure 21.83 Full Alternative Text

x = x^{'} + h and y = y^{'} + k

$x = x^{'} + h and y = y^{'} + k$ (21.26)

Equation (21.26) can also be written in the form

x^{'} = x - h and y^{'} = y - k

$x^{'} = x - h and y^{'} = y - k$ (21.27)

EXAMPLE 1 Find an equation—given vertex and focus

Find the equation of the parabola with vertex (2, 4) and focus (4, 4).

If we let the origin of the $x^{'} y^{'} -coordinate$ $x^{'} y^{'} -coordinate$ system be the point (2, 4), then the point (4, 4) is the point (2, 0) in the $x^{'} y^{'} -system .$ $x^{'} y^{'} -system .$ This means $p = 2$ $p = 2$ and $4 p = 8.$ $4 p = 8.$ See Fig. 21.84. In the $x^{'} y^{'} -system,$ $x^{'} y^{'} -system,$ the equation is

A rightward opening parabola has vertex (2, 4) and focus (4, 4). An x prime y prime plane places (2, 4) at its origin. — Fig. 21.84

{(y^{'})}^{2} = 8 (x^{'})

${(y^{'})}^{2} = 8 (x^{'})$

Using Eqs. (21.27), we have

Left parenthesis y minus 4 right parenthesis squared = 8 left parenthesis x minus 2 right parenthesis. The terms 4 and 2 are labeled, (2, 4).

as the equation of the parabola in the xy-coordinate system.

Following the method of Example 1, by writing the equation of the curve in the $x^{'} y^{'} - system$ $x^{'} y^{'} - system$ and then using Eqs. (21.27), we have the following more general forms of the equations of the parabola, ellipse, and hyperbola.

\begin{array}{l} Parabola, vertex (h, k) : & {(y - k)}^{2} = 4 p (x - h) & (axis parallel to x -axis) \end{array}

$\begin{array}{l} Parabola, vertex (h, k) : & {(y - k)}^{2} = 4 p (x - h) & (axis parallel to x -axis) \end{array}$ (21.28)

\begin{array}{l} {(x - h)}^{2} = 4 p (y - k) & (axis parallel to y -axis) \end{array}

$\begin{array}{l} {(x - h)}^{2} = 4 p (y - k) & (axis parallel to y -axis) \end{array}$ (21.29)

\begin{array}{l} Ellipse, center (h, k) : & \frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}} = 1 & (major axis parallel to x -axis) \end{array}

$\begin{array}{l} Ellipse, center (h, k) : & \frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}} = 1 & (major axis parallel to x -axis) \end{array}$ (21.30)

\begin{array}{l} \frac{{(y - k)}^{2}}{a^{2}} + \frac{{(x - h)}^{2}}{b^{2}} = 1 & (major axis parallel to y -axis) \end{array}

$\begin{array}{l} \frac{{(y - k)}^{2}}{a^{2}} + \frac{{(x - h)}^{2}}{b^{2}} = 1 & (major axis parallel to y -axis) \end{array}$ (21.31)

\begin{array}{l} Hyperbola, center (h, k) : & \frac{{(x - h)}^{2}}{a^{2}} - \frac{{(y - k)}^{2}}{b^{2}} = 1 & (transverse axis parallel to x -axis) \end{array}

$\begin{array}{l} Hyperbola, center (h, k) : & \frac{{(x - h)}^{2}}{a^{2}} - \frac{{(y - k)}^{2}}{b^{2}} = 1 & (transverse axis parallel to x -axis) \end{array}$ (21.32)

\begin{array}{l} \frac{{(y - k)}^{2}}{a^{2}} - \frac{{(x - h)}^{2}}{b^{2}} = 1 & (transverse axis parallel to y -axis) \end{array}

$\begin{array}{l} \frac{{(y - k)}^{2}}{a^{2}} - \frac{{(x - h)}^{2}}{b^{2}} = 1 & (transverse axis parallel to y -axis) \end{array}$ (21.33)

EXAMPLE 2 Describing a curve—given equation

Describe the curve of the equation

\frac{{(x - 3)}^{2}}{25} + \frac{{(y + 2)}^{2}}{9} = 1

$\frac{{(x - 3)}^{2}}{25} + \frac{{(y + 2)}^{2}}{9} = 1$

We see that this equation fits the form of Eq. (21.30) with $h = 3$ $h = 3$ and $k = - 2.$ $k = - 2.$ It is the equation of an ellipse with its center at $(3, - 2)$ $(3, - 2)$ and its major axis parallel to the x-axis. The semimajor axis is $a = 5,$ $a = 5,$ and the semiminor axis is $b = 3.$ $b = 3.$ The ellipse is shown in Fig. 21.85.

A horizontal ellipse centered at (3, negative 2) has major vertices (negative 2, negative 2) and (8, negative 2), and minor vertices (3, 1) and (3, negative 5). Translated axes x prime and y prime have an origin at (3, negative 2). — Fig. 21.85

EXAMPLE 3 Finding the center of a hyperbola

Find the center of the hyperbola $2 x^{2} - y^{2} - 4 x - 4 y - 4 = 0.$ $2 x^{2} - y^{2} - 4 x - 4 y - 4 = 0.$

To analyze this curve, we first complete the square in the x-terms and in the y-terms. This will allow us to recognize the values of h and k.

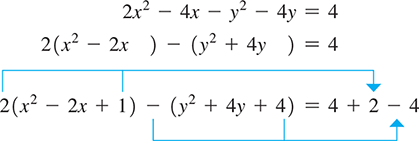
An equation for finding the center of a hyperbola.

21.7-2 Full Alternative Text

NOTE

[We note here that when we added 1 to complete the square of the x-terms within the parentheses, we were actually adding 2 to the left side. Thus, we added 2 to the right side. Similarly, when we added 4 to the y-terms within the parentheses, we were actually subtracting 4 from the left side. Thus, we subtract 4 from the right side.]

Continuing, we have

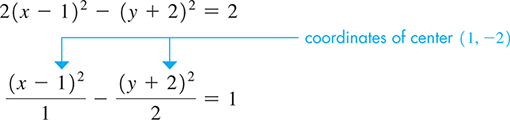
An equation for finding the center of a hyperbola, continued.

21.7-2 Full Alternative Text

Therefore, the center of the hyperbola is $(1, - 2) .$ $(1, - 2) .$ See Fig. 21.86.

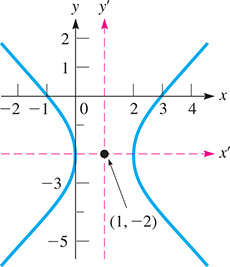
A horizontal hyperbola centered at (1, negative 2) has vertices (0, negative 2) and (2, negative 2). Translated axes x prime and y prime have an origin at (1, negative 2). — Fig. 21.86

EXAMPLE 4 Translation of axes—surface area of a beaker

Cylindrical glass beakers are to be made with a height of 3 in. Express the surface area in terms of the radius of the base and sketch the curve.

The total surface area S of a beaker is the sum of the area of the base and the lateral surface area of the side. In general, S in terms of the radius r of the base and height h of the side is $S = π r^{2} + 2 π r h .$ $S = π r^{2} + 2 π r h .$ Because $h = 3 in .,$ $h = 3 in .,$ we have

S = π r^{2} + 6 π r

$S = π r^{2} + 6 π r$

which is the desired relationship. See Fig. 21.87.

A cylinder with height h = 3 inches and radius r. — Fig. 21.87

To analyze the equation relating S and r, we complete the square of the r terms:

Analysis of the equation relating S and r.

21.7-2 Full Alternative Text

This represents a parabola with vertex $(- 3, - 9 π) .$ $(- 3, - 9 π) .$ See Fig. 21.88. Because $4 p = 1 / π, p = 1 / (4 π)$ $4 p = 1 / π, p = 1 / (4 π)$ and the focus is at $(- 3, \frac{1}{4 π} - 9 π)$ $(- 3, \frac{1}{4 π} - 9 π)$ . The part of the graph for negative r is dashed because only positive values have meaning.

An upward opening parabola falls through (negative 6, 0) to vertex (3, negative 9 pi), then rises through (0, 0). The parabola left of (0, 0) is dashed. — Fig. 21.88

Exercises 21.7

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting problem.

In Example 2, change $y + 2$ $y + 2$ to $y - 2$ $y - 2$ and change the sign before the second term from $+$ $+$ to $- .$ $- .$ Then describe and sketch the curve.
In Example 3, change the fourth and fifth terms from $- 4 y - 4$ $- 4 y - 4$ to $+ 6 y - 9$ $+ 6 y - 9$ and then find the center.

In Exercises 3–10, describe the curve represented by each equation. Identify the type of curve and its center (or vertex if it is a parabola). Sketch each curve.

${(y - 2)}^{2} = 4 (x + 1)$ ${(y - 2)}^{2} = 4 (x + 1)$
$\frac{{(x + 4)}^{2}}{4} + {(y - 1)}^{2} = 1$ $\frac{{(x + 4)}^{2}}{4} + {(y - 1)}^{2} = 1$
$\frac{{(x - 1)}^{2}}{4} - \frac{{(y - 2)}^{2}}{25} = 1$ $\frac{{(x - 1)}^{2}}{4} - \frac{{(y - 2)}^{2}}{25} = 1$
${(y + 5)}^{2} = - 8 (x - 2)$ ${(y + 5)}^{2} = - 8 (x - 2)$
${(x + 1)}^{2} + \frac{y^{2}}{36} = 1$ ${(x + 1)}^{2} + \frac{y^{2}}{36} = 1$
$\frac{{(y - 4)}^{2}}{49} - \frac{{(x + 2)}^{2}}{4} = 1$ $\frac{{(y - 4)}^{2}}{49} - \frac{{(x + 2)}^{2}}{4} = 1$
${(x + 3)}^{2} = - 12 (y - 1)$ ${(x + 3)}^{2} = - 12 (y - 1)$
$\frac{x^{2}}{0.16} + \frac{{(y + 1)}^{2}}{0.25} = 1$ $\frac{x^{2}}{0.16} + \frac{{(y + 1)}^{2}}{0.25} = 1$

In Exercises 11–22, find the equation of each of the curves described by the given information.

Parabola: vertex $(- 1, 3),$ $(- 1, 3),$ focus $(- 1, 6)$ $(- 1, 6)$
Parabola: focus $(4, - 4),$ $(4, - 4),$ directrix $y = - 2$ $y = - 2$
Parabola: axis, directrix are coordinate axes, focus (10, 0)
Parabola: vertex (4, 4), vertical directrix, passes through (0, 1)
Ellipse: center $(- 2, 2),$ $(- 2, 2),$ focus $(- 5, 2),$ $(- 5, 2),$ vertex $(- 7, 2)$ $(- 7, 2)$
Ellipse: center (0, 3), focus (12, 3), major axis 26 units
Ellipse: center $(- 2, 1),$ $(- 2, 1),$ vertex $(- 2, 5),$ $(- 2, 5),$ passes through (0, 1)
Ellipse: foci $(1, - 2)$ $(1, - 2)$ and (1, 10), minor axis 5 units
Hyperbola: vertex $(- 1, 1),$ $(- 1, 1),$ focus $(- 1, 4),$ $(- 1, 4),$ center $(- 1, 2)$ $(- 1, 2)$
Hyperbola: foci (2, 1) and (8, 1), conjugate axis 6 units
Hyperbola: vertices (2, 1) and $(- 4, 1),$ $(- 4, 1),$ focus $(- 6, 1)$ $(- 6, 1)$
Hyperbola: center $(1, - 4),$ $(1, - 4),$ focus (1, 1), transverse axis 8 units

In Exercises 23–40, determine the center (or vertex if the curve is a parabola) of the given curve. Sketch each curve.

$x^{2} + 2 x - 4 y - 3 = 0$ $x^{2} + 2 x - 4 y - 3 = 0$
$y^{2} - 2 x - 2 y - 9 = 0$ $y^{2} - 2 x - 2 y - 9 = 0$
$x^{2} + 4 y = 24$ $x^{2} + 4 y = 24$
$x^{2} + 4 y^{2} = 32 y$ $x^{2} + 4 y^{2} = 32 y$
$4 x^{2} + 9 y^{2} + 24 x = 0$ $4 x^{2} + 9 y^{2} + 24 x = 0$
$2 x^{2} + y^{2} + 8 x = 8 y$ $2 x^{2} + y^{2} + 8 x = 8 y$
$9 x^{2} - y^{2} + 8 y = 7$ $9 x^{2} - y^{2} + 8 y = 7$
$2 x^{2} - 4 x = 9 y - 2$ $2 x^{2} - 4 x = 9 y - 2$
$5 x^{2} - 4 y^{2} + 20 x + 8 y = 4$ $5 x^{2} - 4 y^{2} + 20 x + 8 y = 4$
$0.04 x^{2} + 0.16 y^{2} = 0.01 y$ $0.04 x^{2} + 0.16 y^{2} = 0.01 y$
$4 x^{2} - y^{2} + 32 x + 10 y + 35 = 0$ $4 x^{2} - y^{2} + 32 x + 10 y + 35 = 0$
$2 x^{2} + 2 y^{2} - 24 x + 16 y + 95 = 0$ $2 x^{2} + 2 y^{2} - 24 x + 16 y + 95 = 0$
$16 x^{2} + 25 y^{2} - 32 x + 100 y - 284 = 0$ $16 x^{2} + 25 y^{2} - 32 x + 100 y - 284 = 0$
$9 x^{2} - 16 y^{2} - 18 x + 96 y - 279 = 0$ $9 x^{2} - 16 y^{2} - 18 x + 96 y - 279 = 0$
$5 x^{2} - 3 y^{2} + 95 = 40 x$ $5 x^{2} - 3 y^{2} + 95 = 40 x$
$5 x^{2} + 12 y + 18 = 2 y^{2}$ $5 x^{2} + 12 y + 18 = 2 y^{2}$
$9 x^{2} + 9 y^{2} + 14 = 6 x + 24 y$ $9 x^{2} + 9 y^{2} + 14 = 6 x + 24 y$
$4 y^{2} + 29 = 15 x + 12 y$ $4 y^{2} + 29 = 15 x + 12 y$

In Exercises 41–54, solve the given problems.

Find the equation of the hyperbola with asymptotes $x - y = - 1$ $x - y = - 1$ and $x + y = - 3$ $x + y = - 3$ and vertex $(3, - 1) .$ $(3, - 1) .$
The circle $x^{2} + y^{2} + 4 x - 5 = 0$ $x^{2} + y^{2} + 4 x - 5 = 0$ passes through the foci and the ends of the minor axis of an ellipse that has its major axis along the x-axis. Find the equation of the ellipse.
The vertex and focus of one parabola are, respectively, the focus and vertex of a second parabola. Find the equation of the first parabola, if $y^{2} = 4 x$ $y^{2} = 4 x$ is the equation of the second.
Identify the curve represented by $4 y^{2} - x^{2} - 6 x - 2 y = 14$ $4 y^{2} - x^{2} - 6 x - 2 y = 14$ and view it on a graphing calculator.
What is the general form of the equation of a family of parabolas if each vertex and focus is on the x-axis?
What is the general form of the equation of a family of ellipses with foci on the y-axis if each passes through the origin?
If (a,3) is a point on the parabola $y = x^{2} + 2 x,$ $y = x^{2} + 2 x,$ what is a?
The vertical cross-section of a culvert under a road is elliptical. The culvert is 18 m wide and 12 m high. Find an equation to represent the perimeter of the culvert with the origin at road level and 2.0 m above the top of the culvert. See Fig. 21.89.

Fig. 21.89
An electric current (in A) is $i = 2 + \sin (2 π t - \frac{π}{3}) .$ $i = 2 + \sin (2 π t - \frac{π}{3}) .$ What is the equation for the current if the origin of the $(t^{'}, i^{'})$ $(t^{'}, i^{'})$ system is taken as $(\frac{1}{6}, 2)$ $(\frac{1}{6}, 2)$ of the (t, i) system?
The stopping distance d (in ft) of a car traveling at v mi/h is represented by $d = 0.05 v^{2} + v .$ $d = 0.05 v^{2} + v .$ Where is the vertex of the parabola that represents d?
The stream from a fire hose follows a parabolic curve and reaches a maximum height of 60 ft at a horizontal distance of 95 ft from the nozzle. Find the equation that represents the stream, with the origin at the nozzle. Sketch the graph.
For a constant capacitive reactance and a constant resistance, sketch the graph of the impedance and inductive reactance (as abscissas) for an alternating-current circuit. (See Section 12.7.)
Two wheels in a friction drive assembly are equal ellipses, as shown in Fig. 21.90. They are always in contact, with the left wheel fixed in position and the right wheel able to move horizontally. Find the equation that can be used to represent the circumference of each wheel in the position shown.

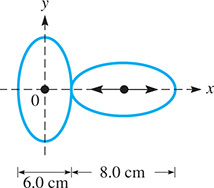
Fig. 21.90
An agricultural test station is to be divided into rectangular sections, each with a perimeter of 480 m. Express the area A of each section in terms of its width w and identify the type of curve represented. Sketch the graph of A as a function of w. For what value of w is A the greatest?

Answer to Practice Exercise

$C (2, - 3), F (1, - 3), F (3, - 3)$ $C (2, - 3), F (1, - 3), F (3, - 3)$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 21.7 Translation of Axes

Create new playlist

Sign In

Sign Up

Table of Contents for
21.7 Translation of Axes