Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

20.4 Half-Angle Formulas

Formula for $\sin (α / 2)$ $\sin (α / 2)$ • Formula for $\cos (α / 2)$ $\cos (α / 2)$

If we let $θ = α / 2$ $θ = α / 2$ in the identity $\cos 2 θ = 1 - 2 \sin^{2} θ$ $\cos 2 θ = 1 - 2 \sin^{2} θ$ and then solve for $\sin (α / 2),$ $\sin (α / 2),$

\sin \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{2}}

$\sin \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{2}}$ (20.26)

Also, with the same substitution in the identity $\cos 2 θ = 2 \cos^{2} θ - 1,$ $\cos 2 θ = 2 \cos^{2} θ - 1,$ which is then solved for $\cos (α / 2),$ $\cos (α / 2),$ we have

\cos \frac{α}{2} = \pm \sqrt{\frac{1 + \cos α}{2}}

$\cos \frac{α}{2} = \pm \sqrt{\frac{1 + \cos α}{2}}$ (20.27)

CAUTION

In each of Eqs. (20.26) and (20.27), the sign chosen depends on the quadrant in which $\frac{α}{2}$ $\frac{α}{2}$ lies.

EXAMPLE 1 Evaluation using cos(α / 2) formula

We can find $\cos 165 °$ $\cos 165 °$ by using the relation

\begin{array}{rcll} \cos 165 ° & = & - \sqrt{\frac{1 + \cos 330 °}{2}} & using Eq . (20.27) \\ = & - \sqrt{\frac{1 + 0.8660}{2}} & = - 0.9659 \end{array}

$\begin{array}{rcll} \cos 165 ° & = & - \sqrt{\frac{1 + \cos 330 °}{2}} & using Eq . (20.27) \\ = & - \sqrt{\frac{1 + 0.8660}{2}} & = - 0.9659 \end{array}$

Here, the minus sign is used, since $165 °$ $165 °$ is in the second quadrant, and the cosine of a second-quadrant angle is negative.

EXAMPLE 2 Evaluation using sin(α / 2) formula

Simplify $\sqrt{\frac{1 - \cos 114 °}{2}}$ $\sqrt{\frac{1 - \cos 114 °}{2}}$ by expressing the result in terms of one-half the given angle. Then, using a calculator, show that the values are equal.

We note that the given expression fits the form of the right side of Eq. (20.26), which means that

\sqrt{\frac{1 - \cos 114 °}{2}} = \sin \frac{1}{2} (114 °) = \sin 57 °

$\sqrt{\frac{1 - \cos 114 °}{2}} = \sin \frac{1}{2} (114 °) = \sin 57 °$

Using a calculator shows that

\sqrt{\frac{1 - \cos 114 °}{2}} = 0.8386705679 and \sin 57 ° = 0.8386705679

$\sqrt{\frac{1 - \cos 114 °}{2}} = 0.8386705679 and \sin 57 ° = 0.8386705679$

which verifies the equation for these values.

EXAMPLE 3 Simplification using cos(α / 2) formula

Simplify the expression $\sqrt{\frac{9 + 9 \cos 6 x}{2}} .$ $\sqrt{\frac{9 + 9 \cos 6 x}{2}} .$

\begin{array}{rcll} \sqrt{\frac{9 + 9 \cos 6 x}{2}} & = & \sqrt{\frac{9 (1 + \cos 6 x)}{2}} & = 3 \sqrt{\frac{1 + \cos 6 x}{2}} \\ = & 3 \cos \frac{1}{2} (6 x) & using Eq . (20.27) with α = 6 x \\ = & 3 \cos 3 x \end{array}

$\begin{array}{rcll} \sqrt{\frac{9 + 9 \cos 6 x}{2}} & = & \sqrt{\frac{9 (1 + \cos 6 x)}{2}} & = 3 \sqrt{\frac{1 + \cos 6 x}{2}} \\ = & 3 \cos \frac{1}{2} (6 x) & using Eq . (20.27) with α = 6 x \\ = & 3 \cos 3 x \end{array}$

Noting the original expression, we see that cos 3x cannot be negative.

EXAMPLE 4 Trig identity with sin(α / 2)—kinetic theory of gases

In the kinetic theory of gases, the expression $\sqrt{{(1 - \cos α)}^{2} + \sin^{2} α}$ $\sqrt{{(1 - \cos α)}^{2} + \sin^{2} α}$ is found. Show that this expression equals $2 \sin \frac{1}{2} α :$ $2 \sin \frac{1}{2} α :$

\begin{array}{rcll} \sqrt{{(1 - \cos α)}^{2} + \sin^{2} α} & = & \sqrt{1 - 2 \cos α + \cos^{2} α + \sin^{2} α} & expanding \\ = & \sqrt{1 - 2 \cos α + 1} & using Eq . (20.26) \\ = & \sqrt{2 - 2 \cos α} \\ = & \sqrt{2 (1 - \cos α)} & factoring \end{array}

$\begin{array}{rcll} \sqrt{{(1 - \cos α)}^{2} + \sin^{2} α} & = & \sqrt{1 - 2 \cos α + \cos^{2} α + \sin^{2} α} & expanding \\ = & \sqrt{1 - 2 \cos α + 1} & using Eq . (20.26) \\ = & \sqrt{2 - 2 \cos α} \\ = & \sqrt{2 (1 - \cos α)} & factoring \end{array}$

This last expression is very similar to that for $\sin \frac{1}{2} α,$ $\sin \frac{1}{2} α,$ except that no 2 appears in the denominator. Therefore, multiplying the numerator and the denominator under the radical by 2 leads to the solution:

\begin{array}{rcl} \sqrt{2 (1 - \cos α)} & = & \sqrt{\frac{4 (1 - \cos α)}{2}} = 2 \sqrt{\frac{1 - \cos α}{2}} \\ = & 2 \sin \frac{1}{2} α & \begin{array}{l} using Eq . (20.26) \end{array} \end{array}

$\begin{array}{rcl} \sqrt{2 (1 - \cos α)} & = & \sqrt{\frac{4 (1 - \cos α)}{2}} = 2 \sqrt{\frac{1 - \cos α}{2}} \\ = & 2 \sin \frac{1}{2} α & \begin{array}{l} using Eq . (20.26) \end{array} \end{array}$

Noting the original expression, we see that $\sin \frac{1}{2} α$ $\sin \frac{1}{2} α$ cannot be negative.

EXAMPLE 5 Evaluation using cos(α / 2) formula

Given that $\tan α = \frac{8}{15} (180 ° < α < 270 °),$ $\tan α = \frac{8}{15} (180 ° < α < 270 °),$ find $\cos (\frac{α}{2}) .$ $\cos (\frac{α}{2}) .$

Knowing that $\tan α = \frac{8}{15}$ $\tan α = \frac{8}{15}$ for a third-quadrant angle, we determine from Fig. 20.20 that $\cos α = - \frac{15}{17} .$ $\cos α = - \frac{15}{17} .$ This means

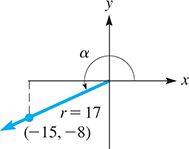
The terminal side of a position angle passes through (negative 15, negative 8) with length r = 17, and at counterclockwise angle alpha in quadrant 3. — Fig. 20.20

\begin{array}{rcl} \cos \frac{α}{2} & = & - \sqrt{\frac{1 + (- 15/17)}{2}} = - \sqrt{\frac{2}{34}} & using Eq . (20.27) \\ = & - \frac{1}{17} \sqrt{17} = - 0.2425 \end{array}

$\begin{array}{rcl} \cos \frac{α}{2} & = & - \sqrt{\frac{1 + (- 15/17)}{2}} = - \sqrt{\frac{2}{34}} & using Eq . (20.27) \\ = & - \frac{1}{17} \sqrt{17} = - 0.2425 \end{array}$

Because $180 ° < α < 270 °,$ $180 ° < α < 270 °,$ we know that $90 ° < \frac{α}{2} < 135 °$ $90 ° < \frac{α}{2} < 135 °$ and therefore $\frac{α}{2}$ $\frac{α}{2}$ is in the second quadrant. Because the cosine is negative for second-quadrant angles, we use the negative value of the radical.

EXAMPLE 6 Simplification—calculator verification

Show that $2 \cos^{2} \frac{x}{2} - \cos x = 1 .$ $2 \cos^{2} \frac{x}{2} - \cos x = 1 .$

The first step is to substitute for $\cos \frac{x}{2},$ $\cos \frac{x}{2},$ which will result in each term on the left being in terms of x and no $\frac{x}{2}$ $\frac{x}{2}$ terms will exist. This might allow us to combine terms. So we perform this operation, and we have for the left side

\begin{array}{rcll} 2 \cos^{2} \frac{x}{2} - \cos x & = & 2 (\frac{1 + \cos x}{2}) - \cos x & \begin{array}{l} using Eq . (20.27) with \\ both sides squared \end{array} \\ = & 1 + \cos x - \cos x = 1 \end{array}

$\begin{array}{rcll} 2 \cos^{2} \frac{x}{2} - \cos x & = & 2 (\frac{1 + \cos x}{2}) - \cos x & \begin{array}{l} using Eq . (20.27) with \\ both sides squared \end{array} \\ = & 1 + \cos x - \cos x = 1 \end{array}$

From Fig. 20.21, we verify that the graph of $y_{1} = 2 {[\cos (x / 2)]}^{2} - \cos x$ $y_{1} = 2 {[\cos (x / 2)]}^{2} - \cos x$ is the same as the graph of $y_{2} = 1 .$ $y_{2} = 1 .$

A horizontal line passes through (0, 1). Part of the line is red and part is blue. — Fig. 20.21

EXAMPLE 7 Formulas for other functions of α / 2

We can find relations for other functions of $\frac{α}{2}$ $\frac{α}{2}$ by expressing these functions in terms of $\sin (\frac{α}{2})$ $\sin (\frac{α}{2})$ and $\cos (\frac{α}{2}) .$ $\cos (\frac{α}{2}) .$ For example,

\begin{array}{rcl} \sec \frac{α}{2} & = & \frac{1}{\cos \frac{α}{2}} = \pm \frac{1}{\sqrt{\frac{1 + \cos α}{2}}} & using Eq . (20.27) \\ = & \pm \sqrt{\frac{2}{1 + \cos α}} \end{array}

$\begin{array}{rcl} \sec \frac{α}{2} & = & \frac{1}{\cos \frac{α}{2}} = \pm \frac{1}{\sqrt{\frac{1 + \cos α}{2}}} & using Eq . (20.27) \\ = & \pm \sqrt{\frac{2}{1 + \cos α}} \end{array}$

EXERCISES 20.4

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the given problem.

In Example 2, change the $-$ $-$ sign in the numerator to $+ .$ $+ .$
In Example 5, change $\frac{8}{15} (180 ° < α < 270 °)$ $\frac{8}{15} (180 ° < α < 270 °)$ to $- \frac{8}{15} (270 ° < α < 360 °) .$ $- \frac{8}{15} (270 ° < α < 360 °) .$

In Exercises 3–8, use the half-angle formulas to evaluate the given functions.

cos 15°
sin 22.5°
sin 105°
cos 112.5°
$\cos \frac{3 π}{8}$ $\cos \frac{3 π}{8}$
$\sin \frac{11 π}{12}$ $\sin \frac{11 π}{12}$

In Exercises 9–12, simplify the given expressions by giving the results in terms of one-half the given angle. Then use a calculator to verify the result.

$\sqrt{\frac{1 - \cos 236 °}{2}}$ $\sqrt{\frac{1 - \cos 236 °}{2}}$
$\sqrt{\frac{1 + \cos 98 °}{2}}$ $\sqrt{\frac{1 + \cos 98 °}{2}}$
$\sqrt{\frac{1 + \cos 96 °}{2}}$ $\sqrt{\frac{1 + \cos 96 °}{2}}$
$\sqrt{\frac{1 - \cos 328 °}{2}}$ $\sqrt{\frac{1 - \cos 328 °}{2}}$

In Exercises 13–20, simplify the given expressions.

$\sqrt{\frac{1 - \cos 8 x}{2}}$ $\sqrt{\frac{1 - \cos 8 x}{2}}$
$\sqrt{\frac{4 + 4 \cos 8 β}{8}}$ $\sqrt{\frac{4 + 4 \cos 8 β}{8}}$
$\sqrt{\frac{1 + \cos 6 x}{2}}$ $\sqrt{\frac{1 + \cos 6 x}{2}}$
$\sqrt{2 - 2 \cos 64 x}$ $\sqrt{2 - 2 \cos 64 x}$
$\sqrt{4 - 4 \cos 10 θ}$ $\sqrt{4 - 4 \cos 10 θ}$
$\sqrt{18 + 18 \cos 1.4 x}$ $\sqrt{18 + 18 \cos 1.4 x}$
$2 \sin^{2} \frac{x}{2} + \cos x$ $2 \sin^{2} \frac{x}{2} + \cos x$
$2 \cos^{2} \frac{θ}{2} \sec θ$ $2 \cos^{2} \frac{θ}{2} \sec θ$

In Exercises 21–24, evaluate the indicated functions.

Find the value of $\sin (\frac{α}{2})$ $\sin (\frac{α}{2})$ if $\cos α = \frac{12}{13} (0 ° < α < 90 °) .$ $\cos α = \frac{12}{13} (0 ° < α < 90 °) .$
Find the value of $\cos (\frac{α}{2})$ $\cos (\frac{α}{2})$ if $\sin α = - \frac{4}{5} (180 ° < α < 270 °) .$ $\sin α = - \frac{4}{5} (180 ° < α < 270 °) .$
Find the value of $\cos (\frac{α}{2})$ $\cos (\frac{α}{2})$ if $\tan α = - 0.2917 (90 ° < α < 180 °) .$ $\tan α = - 0.2917 (90 ° < α < 180 °) .$
Find the value of $\sin (\frac{α}{2})$ $\sin (\frac{α}{2})$ if $\cos α = 0.4706 (270 ° < α < 360 °) .$ $\cos α = 0.4706 (270 ° < α < 360 °) .$

In Exercises 25–28, derive the required expressions.

Derive an expression for $\csc (\frac{α}{2})$ $\csc (\frac{α}{2})$ in terms of $\sec α$ $\sec α$
Derive an expression for $\sec (\frac{α}{2})$ $\sec (\frac{α}{2})$ in terms of $\sec α .$ $\sec α .$
Derive an expression for $\tan (\frac{α}{2})$ $\tan (\frac{α}{2})$ in terms of $\sin α$ $\sin α$ and $\cos α .$ $\cos α .$
Derive an expression for $\cot (\frac{α}{2})$ $\cot (\frac{α}{2})$ in terms of $\sin α$ $\sin α$ and $\cos α .$ $\cos α .$

In Exercises 29–32, prove the given identities.

$\sin \frac{α}{2} = \frac{1 - \cos α}{2 \sin \frac{α}{2}}$ $\sin \frac{α}{2} = \frac{1 - \cos α}{2 \sin \frac{α}{2}}$
$\cos \frac{θ}{2} = \frac{\sin θ}{2 \sin \frac{θ}{2}}$ $\cos \frac{θ}{2} = \frac{\sin θ}{2 \sin \frac{θ}{2}}$
$2 \cos \frac{x}{2} = (1 + \cos x) \sec \frac{x}{2}$ $2 \cos \frac{x}{2} = (1 + \cos x) \sec \frac{x}{2}$
$\cos^{2} \frac{x}{2} [1 + {(\frac{\sin x}{1 + \cos x})}^{2}] = 1$ $\cos^{2} \frac{x}{2} [1 + {(\frac{\sin x}{1 + \cos x})}^{2}] = 1$

In Exercises 33–36, verify each identity by comparing the graph of the left side with the graph of the right side on a calculator.

$2 \sin^{2} \frac{α}{2} - \cos^{2} \frac{α}{2} = \frac{1 - 3 \cos α}{2}$ $2 \sin^{2} \frac{α}{2} - \cos^{2} \frac{α}{2} = \frac{1 - 3 \cos α}{2}$
$\cos^{2} \frac{A}{2} - \sin^{2} \frac{A}{2} = \frac{\sin 2 A}{2 \sin A}$ $\cos^{2} \frac{A}{2} - \sin^{2} \frac{A}{2} = \frac{\sin 2 A}{2 \sin A}$
$2 \sin^{2} \frac{θ}{2} = \frac{\sin^{2} θ}{1 + \cos θ}$ $2 \sin^{2} \frac{θ}{2} = \frac{\sin^{2} θ}{1 + \cos θ}$
$\tan \frac{α}{2} = \frac{\sin α}{1 + \cos α}$ $\tan \frac{α}{2} = \frac{\sin α}{1 + \cos α}$

In Exercises 37–48, use the half-angle formulas to solve the given problems.

Find $\tan θ$ $\tan θ$ if $\sin (θ / 2) = 3/5 .$ $\sin (θ / 2) = 3/5 .$
In a right triangle with sides and angles as shown in Fig. 20.22, show that $\sin^{2} \frac{A}{2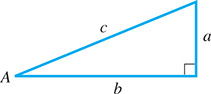} = \frac{c - b}{2 c} .$ $\sin^{2} \frac{A}{2} = \frac{c - b}{2 c} .$

Fig. 20.22
Find the exact value of $\tan 22.5 °$ $\tan 22.5 °$ using half-angle formulas.
If $180 ° < θ < 270 °$ $180 ° < θ < 270 °$ and $\tan (θ / 2) = - π / 3,$ $\tan (θ / 2) = - π / 3,$ find $\sin θ .$ $\sin θ .$
If $90 ° < θ < 180 °$ $90 ° < θ < 180 °$ and $\sin θ = 4/5,$ $\sin θ = 4/5,$ find $\cos (θ / 2) .$ $\cos (θ / 2) .$
Find the area of the segment of the circle in Fig. 20.23, expressing the result in terms of $θ / 2 .$ $θ / 2 .$

Fig. 20.23
In finding the path of a sliding particle, the expression $\sqrt{8 - 8 \cos θ}$ $\sqrt{8 - 8 \cos θ}$ is used. Simplify this expression.
In designing track for a railway system, the equation $d = 4 r \sin^{2} \frac{A}{2}$ $d = 4 r \sin^{2} \frac{A}{2}$ is used. Solve for d in terms of cos A.
In electronics, in order to find the root-mean-square current in a circuit, it is necessary to express $\sin^{2} ω t$ $\sin^{2} ω t$ in terms of $\cos 2 ω t .$ $\cos 2 ω t .$ Show how this is done.
In studying interference patterns of radio signals, the expression $2 E^{2} - 2 E^{2} \cos (π - θ)$ $2 E^{2} - 2 E^{2} \cos (π - θ)$ arises. Show that this can be written as $4 E^{2} \cos^{2} (θ / 2) .$ $4 E^{2} \cos^{2} (θ / 2) .$
The index of refraction n, the angle A of a prism, and the minimum angle of deflection $ϕ$ $ϕ$ are related by $n = \frac{\sin \frac{1}{2} (A + ϕ)}{\sin \frac{1}{2} A} .$ $n = \frac{\sin \frac{1}{2} (A + ϕ)}{\sin \frac{1}{2} A} .$

See Fig. 20.24. Show that an equivalent expression is $n = \sqrt{\frac{1 - \cos A \cos ϕ + \sin A \sin ϕ}{1 - \cos A}}$ $n = \sqrt{\frac{1 - \cos A \cos ϕ + \sin A \sin ϕ}{1 - \cos A}}$

$A prism with angle Ay. A light ray passes through the prism opposite angle Ay, refracting at angle phi so that it exits at a different angle than it entered.$
Fig. 20.24
For the structure shown in Fig. 20.25, show that $x = 2 l \sin^{2} \fra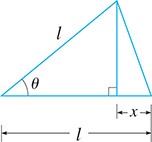c{1}{2} θ .$ $x = 2 l \sin^{2} \frac{1}{2} θ .$

Fig. 20.25

Answers to Practice Exercises

5 sin 2x
$\pm \sqrt{\frac{2}{1 - \cos x}}$ $\pm \sqrt{\frac{2}{1 - \cos x}}$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 20.4 Half-Angle Formulas

Create new playlist

Sign In

Sign Up

Table of Contents for
20.4 Half-Angle Formulas