9.1 Introduction to Vectors

  • Scalars and Vectors • Addition of Vectors • Scalar Multiple of a Vector • Subtraction of Vectors

We deal with many quantities that may be described by a number that shows only the magnitude. These include lengths, areas, time intervals, monetary amounts, and temperatures. Quantities such as these, described only by the magnitude, are known as scalars.

Many other quantities, called vectors, are fully described only when both the magnitude and direction are specified. The following example shows the difference between scalars and vectors.

EXAMPLE 1 Scalars and vectors—speed versus velocity

A jet is traveling at 600 mi/h. From this statement alone, we know only the speed of the jet. Speed is a scalar quantity, and it tells us only the magnitude of the rate. Knowing only the speed of the jet, we know the rate at which it is moving, but we do not know where it is headed.

If the phrase “in a direction 10 °  south of west” is added to the sentence about the jet, we specify the direction of travel as well as the speed. We then know the velocity of the jet; that is the direction of travel as well as the rate at which it is moving. Velocity is a vector quantity.

For an example of the action of two vectors, consider a boat moving on a river. We will assume that the boat is driven by a motor that can move it at 8 mi/h in still water and that the river’s current is going 6 mi/h downstream, as shown in Fig. 9.1. We quickly see that the movement of the boat depends on the direction in which it is headed. If it heads downstream, it moves at 14 mi/h, for the water is moving at 6 mi/h and the boat moves at 8 mi/h with respect to the water. If it heads upstream, however, it moves only at 2 mi/h, because the river is acting directly against the motor. If the boat heads directly across the river, the point it reaches on the other side is not directly opposite the point from which it started. This is so because the river is moving the boat downstream at the same time the boat moves across the river.

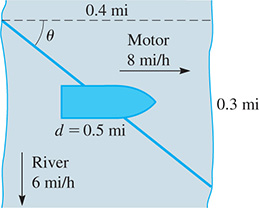
A motor boat travels horizontally right at 8 miles per hour over a river that flows vertically down at 6 miles per hour. The boat travels 0.4 miles to the right and 0.3 miles down river at angle theta to the horizontal.

Fig. 9.1

Checking this last case further, assume that the river is 0.4 mi wide where the boat is crossing. It takes 0.05 h (0.4 mi ÷ 8 mi / h = 0.05 h) to cross. In 0.05 h, the river will carry the boat 0.3 mi (0.05 h × 6 mi / h = 0.3 mi) downstream. This means the boat went 0.3 mi downstream as it went 0.4 mi across the river. From the Pythagorean theorem, we see that it went 0.5 mi from its starting point to its finishing point:

d2 = 0.42 + 0.32 = 0.25d = 0.5 mi

Because the 0.5 mi was traveled in 0.05 h, the magnitude of the velocity (the speed) of the boat was actually

v = dt = 0.5 mi0.05 h = 10 mi / h

Also, note that the direction of this velocity can be represented along a line that makes an angle θ with the line directed directly across the river, as shown in Fig. 9.1. We can find this angle by noting that

tan θ = 0.3 mi0.4 mi = 0.75θ = tan − 10.75 = 37 ° 

Therefore, when headed directly across the river, the boat’s velocity is 10 mi/h directed at an angle of 37 °  downstream from a line directly across the river.

ADDITION OF VECTORS

We have just seen two velocity vectors being added. Note that these vectors are not added the way numbers are added. We must take into account their directions as well as their magnitudes. Reasoning along these lines, let us now define the sum of two vectors.

We will represent a vector quantity by a letter printed in boldface type. The same letter in italic (lightface) type represents the magnitude only. Thus, A is a vector of magnitude A. In handwriting, one usually places an arrow over the letter to represent a vector, such as A→  . 

Let A and B represent vectors directed from O to P and P to Q, respectively (see Fig. 9.2). The vector sum A + B is the vector R, from the initial point O to the terminal point Q. Here, vector R is called the resultant. In general, a resultant is a single vector that is the vector sum of any number of other vectors.

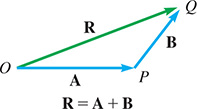
Three vectors.

Fig. 9.2

There are two common methods of adding vectors by means of a diagram. The first method, called the polygon method, is illustrated in Fig. 9.3. To add B to A, shift B parallel to itself until its tail touches the head of A. The vector sum A + B is the resultant vector R, which is drawn from the tail of A to the head of B. When using a diagram to add vectors, it must be drawn with reasonable accuracy.

NOTE

[In using this method, we can move a vector for addition as long as its magnitude and direction remain unchanged. (Because the magnitude and direction specify a vector, two vectors in different locations are considered the same if they have the same magnitude and direction.)]

Adding vectors.

Fig. 9.3

Three or more vectors are added in the same general manner. We place the initial point of the second vector at the terminal point of the first vector, the initial point of the third vector at the terminal point of the second vector, and so on. The resultant is the vector from the initial point of the first vector to the terminal point of the last vector.

NOTE

[The order in which they are added does not matter.]

EXAMPLE 2 Adding vectors—polygon method

The addition of vectors A, B, and C is shown in Fig. 9.4.

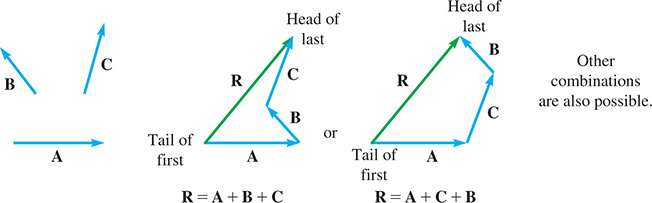
Adding vectors.

Fig. 9.4

Another method that is convenient when only two vectors are being added is the parallelogram method. To use this method, we place the two vectors being added tail to tail and then form a parallelogram that includes those two vectors as sides. The resultant is then the diagonal of the parallelogram, with its initial point being the common initial point of the two vectors being added. This method is illustrated in the following example.

EXAMPLE 3 Adding vectors—parallelogram method

The addition of vectors A and B is shown in Fig. 9.5.

Adding vectors.

Fig. 9.5

If vector C is in the same direction as vector A and C has a magnitude n times that of A, then C = nA ,  where the vector nA is called the scalar multiple of vector A. Note carefully that only the magnitudes of A and 2A are different. Their directions are the same. The addition of scalar multiples of vectors is illustrated in the following example.

NOTE

[This means that 2A is a vector that is twice as long as A but is in the same direction.]

EXAMPLE 4 Scalar multiple of a vector

For vectors A and B in Fig. 9.6, find vector 3A + 2B . 

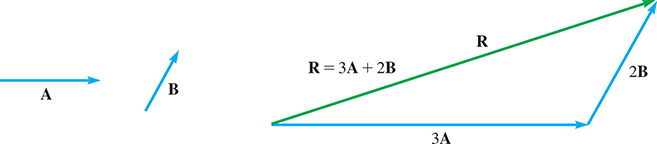
Scalar multiples.

Fig. 9.6

Vector B is subtracted from vector A by reversing the direction of B and proceeding as in vector addition. Vector subtraction is illustrated in the following example.

NOTE

[Thus, A − B = A + ( − B) ,  where the minus sign indicates that vector  − B has the opposite direction of vector B.]

EXAMPLE 5 Subtracting vectors

For vectors A and B in Fig. 9.7, find vector 2A − B . 

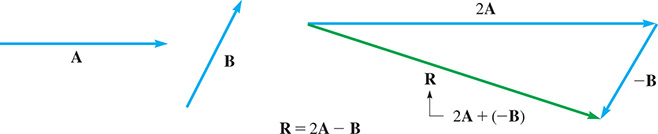
Subtracting vectors.

Fig. 9.7

Among the most important applications of vectors is that of the forces acting on a structure or object. The next example shows the addition of forces by using the parallelogram method.

EXAMPLE 6 Adding vectors—pulling a car

Two persons pull horizontally on ropes attached to a car that is stuck in mud. One person pulls with a force of 500 N directly to the right, while the other person pulls with a force of 350 N at an angle of 40 °  from the first force, as shown in Fig. 9.8(a). Find the resultant force on the car.

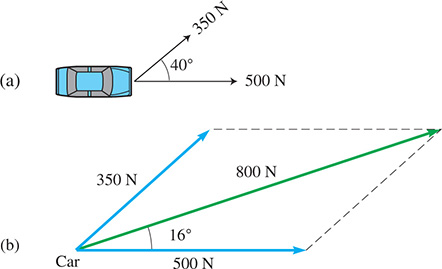
A two-part diagram.

Fig. 9.8

We make a scale drawing of the forces as shown in Fig. 9.8(b), measuring the magnitudes of the forces with a ruler and the angles with a protractor. [The scale drawing of the forces is made larger and with a different scale than that in Fig. 9.8(a) in order to get better accuracy.] We then complete the parallelogram and draw in the diagonal that represents the resultant force. Finally, we find that the resultant force is about 800 N and that it acts at an angle of about 16 °  from the first force.

In addition to force, two other important vector quantities are velocity and displacement. Velocity as a vector is illustrated in Example 1. The following example illustrates the difference between distance and displacement.

NOTE

[The displacement of an object is the change in its position. Displacement is given by the distance from a reference point and the angle from a reference direction.]

EXAMPLE 7 Adding vectors—jet displacement

To avoid a storm, a jet travels at 60 °  north of east from Detroit for 190 mi and then turns to a direction of 10 °  north of east for 280 mi to Ottawa. Find the displacement of Ottawa from Detroit.

We make a scale drawing in Fig. 9.9 to show the route taken by the jet. Measuring distances with a ruler and angles with a protractor, we find that Ottawa is about 420 mi from Detroit, at an angle of about 30 °  north of east. By giving both the magnitude and the direction, we have given the displacement.

Vectors between cities.

Fig. 9.9

If the jet returned directly from Ottawa to Detroit, its displacement from Detroit would be zero, although it traveled a distance of about 890 mi.

EXERCISES 9.1

In Exercises 1–4, find the resultant vectors if the given changes are made in the indicated examples of this section.

  1. In Example 2, what is the resultant of the three vectors if the direction of vector A is reversed?

  2. In Example 4, for vectors A and B, what is vector 2A + 3B ? 

  3. In Example 5, for vectors A and B, what is vector 2B − A ? 

  4. In Example 6, if 20 °  replaces 40 °  ,  what is the resultant force?

In Exercises 5–8, determine whether a scalar or a vector is described in (a) and (b). Explain your answers.

    1. A soccer player runs 15 m from the center of the field.

    2. A soccer player runs 15 m from the center of the field toward the opponents’ goal.

    1. A small-craft warning reports 25 mi/h winds.

    2. A small-craft warning reports 25 mi/h winds from the north.

    1. An arm of an industrial robot pushes with a 10-lb force downward on a part.

    2. A part is being pushed with a 10-lb force by an arm of an industrial robot.

    1. A ballistics test shows that a bullet hit a wall at a speed of 400 ft/s.

    2. A ballistics test shows that a bullet hit a wall at a speed of 400 ft/s perpendicular to the wall.

In Exercises 9–14, add the given vectors by drawing the appropriate resultant.

  1. A vector points right to a vector that points up and left.

  2. A vector points down and right to a vector that points down and left.

  3. A vector points up and left to a vector that points up and right to a third vector that points down and right with half magnitude.

  4. Two vectors form an angle. One vector goes left, and the other goes down and left with greater magnitude.

  5. A vector points up and left. Another vector points down and left.

  6. A vector points vertically down, another points horizontally right, and another points down and left.

In Exercises 15–18, draw the given vectors and find their sum graphically. The magnitude is shown first, followed by the direction as an angle in standard position.

  1. 3.6 cm, 0 ° ; 4.3 cm, 90 ° 

  2. 2.3 cm, 45 ° ; 5.2 cm, 120 ° 

  3. 6.0 cm, 150 ° ; 1.8 cm, 315 ° 

  4. 7.5 cm, 240 ° ; 2.3 cm, 30 ° 

In Exercises 19–40, find the indicated vector sums and differences with the given vectors by means of diagrams. (You might find graph paper to be helpful.)

Five vectors.

  1. A + B

  2. B + C

  3. C + D

  4. D + E

  5. A + C + E

  6. B + D + A

  7. 2A + D + E

  8. B + E + A

  9. B + 3E

  10. A + 2C

  11. 3C + E

  12. 2D + A

  13. A − B

  14. C − D

  15. E − B

  16. C − 2A

  17. 3B + 12A

  18. 2B − 32E

  19. B + 2C − E

  20. A + 2D − 3B

  21. C − B − 34A

  22. D − 2C − 12E

In Exercises 41–48, solve the given problems. Use a ruler and protractor as in Examples 6 and 7.

  1. Two forces that act on an airplane wing are called the lift and the drag. Find the resultant of these forces acting on the airplane wing in Fig. 9.10.

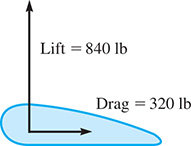
    Vectors on a wing. The vector that points to the right is drag = 320 pounds. The vector that points up is lift = 840 pounds.

    Fig. 9.10

  2. Two electric charges create an electric field intensity, a vector quantity, at a given point. The field intensity is 30 kN/C to the right and 60 kN/C at an angle of 45 °  above the horizontal to the right. Find the resultant electric field intensity at this point.

  3. A ski tow is moving skiers vertically upward at 24 m/min and horizontally at 44 m/min. What is the velocity of the tow?

  4. A jet travels 17 km in a straight line as it also descends 8 km. It then turns upward and travels 10 km in a straight line until it reaches its original altitude, all in an easterly direction. What is the jet’s displacement from its original position?

  5. A driver takes the wrong road at an intersection and travels 4 mi north, then 6 mi east, and finally 10 mi to the southeast to reach the home of a friend. What is the displacement of the friend’s home from the intersection?

  6. A ship travels 20 km in a direction of 30 °  south of east, then turns and goes due south for another 40 km, and finally turns again 30 °  south of east and goes another 20 km. What is the ship’s displacement from its original position?

  7. A rope holds a helium-filled balloon in place with a tension of 510 N at an angle of 80 °  with the ground due to a wind. The weight (a vertical force) of the balloon and contents is 400 N, and the upward buoyant force is 900 N. The wind creates a horizontal force of 90 N on the balloon. What is the resultant force on the balloon?

  8. While unloading a crate weighing 610 N, the chain from a crane supports it with a force of 650 N at an angle of 20 °  from the vertical. What force must a horizontal rope exert on the crate so that the total force (including its weight) on the crate is zero?

Answers to Practice Exercises

  1. Same as R in Fig. 9.4.

  2. (Half scale)

    A vector goes up and left.
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
13.59.136.170