Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1.9 Division of Algebraic Expressions

Dividing Monomials • Dividing by a Monomial • Dividing One Polynomial by Another

To find the quotient of one monomial divided by another, we use the laws of exponents and the laws for dividing signed numbers. Again, the exponents may be combined only if the base is the same.

EXAMPLE 1 Dividing monomials

$\frac{3 c^{7}}{c^{2}} = 3 c^{7 - 2} = 3 c^{5}$ $\frac{3 c^{7}}{c^{2}} = 3 c^{7 - 2} = 3 c^{5}$
.9-6 Full Alternative Text
$\frac{- 6 a^{2} x y^{2}}{2 a x y^{4}} = - (\frac{6}{2}) \frac{a^{2 - 1} x^{1 - 1}}{y^{4 - 2}} = \frac{- 3 a}{y^{2}}$ $\frac{- 6 a^{2} x y^{2}}{2 a x y^{4}} = - (\frac{6}{2}) \frac{a^{2 - 1} x^{1 - 1}}{y^{4 - 2}} = \frac{- 3 a}{y^{2}}$

As shown in illustration (c), we use only positive exponents in the final result unless there are specific instructions otherwise.

From arithmetic, we may show how a multinomial is to be divided by a monomial. When adding fractions $(say \frac{2}{7} and \frac{3}{7}),$ $(say \frac{2}{7} and \frac{3}{7}),$ we have $\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} .$ $\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} .$

Looking at this from right to left, we see that the quotient of a multinomial divided by a monomial is found by dividing each term of the multinomial by the monomial and adding the results. This can be shown as

\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c}

$\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c}$

CAUTION

Be careful: Although $\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c},$ $\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c},$ we must note that $\frac{c}{a + b}$ $\frac{c}{a + b}$ is not $\frac{c}{a} + \frac{c}{b} .$ $\frac{c}{a} + \frac{c}{b} .$

EXAMPLE 2 Dividing by a monomial

Two equations a and b illustrate monomial division.

.9-6 Full Alternative Text

We usually do not write out the middle step as shown in these illustrations. The divisions of the terms of the numerator by the denominator are usually done by inspection (mentally), and the result is shown as it appears in the next example.

NOTE

[Note carefully the last term 1 of the result. When all factors of the numerator are the same as those in the denominator, we are dividing a number by itself, which gives a result of 1.]

EXAMPLE 3 Dividing by a monomial—irrigation pump

The expression $\frac{2 p + v^{2} d + 2 y d g}{2 d g}$ $\frac{2 p + v^{2} d + 2 y d g}{2 d g}$ is used when analyzing the operation of an irrigation pump. Performing the indicated division, we have

\frac{2 p + v^{2} d + 2 y d g}{2 d g} = \frac{p}{d g} + \frac{v^{2}}{2 g} + y

$\frac{2 p + v^{2} d + 2 y d g}{2 d g} = \frac{p}{d g} + \frac{v^{2}}{2 g} + y$

DIVISION OF ONE POLYNOMIAL BY ANOTHER

To divide one polynomial by another, use the following steps.

Arrange the dividend (the polynomial to be divided) and the divisor in descending powers of the variable.
Divide the first term of the dividend by the first term of the divisor. The result is the first term of the quotient.
Multiply the entire divisor by the first term of the quotient and subtract the product from the dividend.
Divide the first term of this difference by the first term of the divisor. This gives the second term of the quotient.
Multiply this term by the entire divisor and subtract the product from the first difference.
Repeat this process until the remainder is zero or of lower degree than the divisor.
Express the answer in the form $quotient + \frac{remainder}{divisor} .$ $quotient + \frac{remainder}{divisor} .$

EXAMPLE 4 Dividing one polynomial by another

Perform the division $(6 x^{2} + x - 2) \div (2 x - 1) .$ $(6 x^{2} + x - 2) \div (2 x - 1) .$

(This division can also be indicated in the fractional form \frac{6 x^{2} + x - 2}{2 x - 1} .)

$(This division can also be indicated in the fractional form \frac{6 x^{2} + x - 2}{2 x - 1} .)$

We set up the division as we would for long division in arithmetic. Then, following the procedure outlined above, we have the following:

.9-6 Full Alternative Text

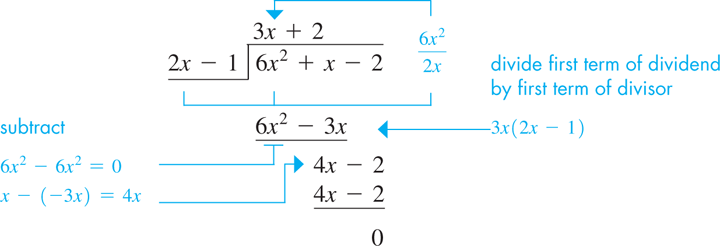
The remainder is zero and the quotient is $3 x + 2.$ $3 x + 2.$ Therefore, the answer is

3 x + 2 + \frac{0}{2 x - 1}, or simply 3 x + 2

$3 x + 2 + \frac{0}{2 x - 1}, or simply 3 x + 2$

EXAMPLE 5 Quotient with a remainder

Perform the division $\frac{8 x^{3} + 4 x^{2} + 3}{4 x^{2} - 1.}$ $\frac{8 x^{3} + 4 x^{2} + 3}{4 x^{2} - 1.}$ Because there is no x-term in the dividend, we should leave space for any x-terms that might arise (which we will show as 0x).

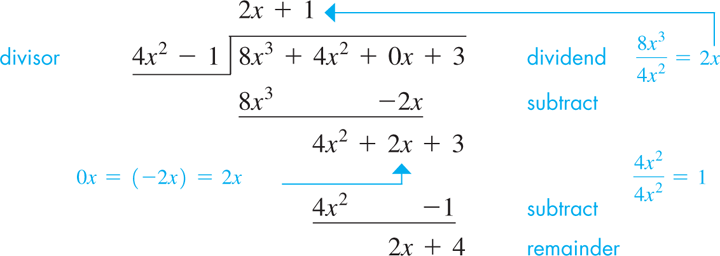
The process of dividing polynomial 6 x squared plus x minus 2 by 2 x minus 1 has 6 steps as follows.

.9-6 Full Alternative Text

Because the degree of the remainder $2 x + 4$ $2 x + 4$ is less than that of the divisor, the long-division process is complete and the answer is $2 x + 1 + \frac{2 x + 4}{4 x^{2} - 1} .$ $2 x + 1 + \frac{2 x + 4}{4 x^{2} - 1} .$

EXERCISES 1.9

In Exercises 1–4, make the given changes in the indicated examples of this section and then perform the indicated divisions.

In Example 1(c), change the denominator to $- 2 a^{2} x y^{5} .$ $- 2 a^{2} x y^{5} .$
In Example 2(b), change the denominator to $2 x y^{2} .$ $2 x y^{2} .$
In Example 4, change the dividend to $6 x^{2} - 7 x + 2.$ $6 x^{2} - 7 x + 2.$
In Example 5, change the sign of the middle term of the numerator from $+$ $+$ to $- .$ $- .$

In Exercises 5–24, perform the indicated divisions.

$\frac{8 x^{3} y^{2}}{- 2 x y}$ $\frac{8 x^{3} y^{2}}{- 2 x y}$
$\frac{- 18 b^{7} c^{3}}{b c^{2}}$ $\frac{- 18 b^{7} c^{3}}{b c^{2}}$
$\frac{- 16 r^{3} t^{5}}{- 4 r^{5} t}$ $\frac{- 16 r^{3} t^{5}}{- 4 r^{5} t}$
$\frac{51 m n^{5}}{17 m^{2} n^{2}}$ $\frac{51 m n^{5}}{17 m^{2} n^{2}}$
$\frac{(15 x^{2} y) (2 x z)}{10 x y}$ $\frac{(15 x^{2} y) (2 x z)}{10 x y}$
$\frac{(5 s T) (8 s^{2} T^{3})}{10 s^{3} T^{2}}$ $\frac{(5 s T) (8 s^{2} T^{3})}{10 s^{3} T^{2}}$
$\frac{(4 a^{3}) {(2 x)}^{2}}{{(4 a x)}^{2}}$ $\frac{(4 a^{3}) {(2 x)}^{2}}{{(4 a x)}^{2}}$
$\frac{12 a^{2} b}{{(3 a b^{2})}^{2}}$ $\frac{12 a^{2} b}{{(3 a b^{2})}^{2}}$
$\frac{3 a^{2} x + 6 x y}{3 x}$ $\frac{3 a^{2} x + 6 x y}{3 x}$
$\frac{2 m^{2} n - 6 m n}{- 2 m}$ $\frac{2 m^{2} n - 6 m n}{- 2 m}$
$\frac{3 r s t - 6 r^{2} s t^{2}}{3 r s}$ $\frac{3 r s t - 6 r^{2} s t^{2}}{3 r s}$
$\frac{- 5 a^{2} n - 10 a n^{2}}{5 a n}$ $\frac{- 5 a^{2} n - 10 a n^{2}}{5 a n}$
$\frac{4 p q^{3} + 8 p^{2} q^{2} - 16 p q^{5}}{4 p q^{2}}$ $\frac{4 p q^{3} + 8 p^{2} q^{2} - 16 p q^{5}}{4 p q^{2}}$
$\frac{a^{2} x_{1} x_{2}^{2} + a x_{1}^{3} - a x_{1}}{a x_{1}}$ $\frac{a^{2} x_{1} x_{2}^{2} + a x_{1}^{3} - a x_{1}}{a x_{1}}$
$\frac{2 π f L - π f R^{2}}{π f R}$ $\frac{2 π f L - π f R^{2}}{π f R}$
$\frac{9 {(a B)}^{4} - 6 a B^{4}}{- 3 a B^{3}}$ $\frac{9 {(a B)}^{4} - 6 a B^{4}}{- 3 a B^{3}}$
$\frac{- 7 a^{2} b + 14 a b^{2} - 21 a^{3}}{14 a^{2} b^{2}}$ $\frac{- 7 a^{2} b + 14 a b^{2} - 21 a^{3}}{14 a^{2} b^{2}}$
$\frac{2 x^{n + 2} + 4 a x^{n}}{2 x^{n}}$ $\frac{2 x^{n + 2} + 4 a x^{n}}{2 x^{n}}$
$\frac{6 y^{2 n} - 4 a y^{n + 1}}{2 y^{n}}$ $\frac{6 y^{2 n} - 4 a y^{n + 1}}{2 y^{n}}$
$\frac{3 a (F + T) b^{2} - (F + T)}{a (F + T)}$ $\frac{3 a (F + T) b^{2} - (F + T)}{a (F + T)}$

In Exercises 25–44, perform the indicated divisions. Express the answer as shown in Example 5 when applicable.

$(x^{2} + 9 x + 20) \div (x + 4)$ $(x^{2} + 9 x + 20) \div (x + 4)$
$(x^{2} + 7 x - 18) \div (x - 2)$ $(x^{2} + 7 x - 18) \div (x - 2)$
$(2 x^{2} + 7 x + 3) \div (x + 3)$ $(2 x^{2} + 7 x + 3) \div (x + 3)$
$(3 t^{2} - 7 t + 4) \div (t - 1)$ $(3 t^{2} - 7 t + 4) \div (t - 1)$
$(x^{2} - 3 x + 2) \div (x - 2)$ $(x^{2} - 3 x + 2) \div (x - 2)$
$(2 x^{2} - 5 x - 7) \div (x + 1)$ $(2 x^{2} - 5 x - 7) \div (x + 1)$
$(x - 14 x^{2} + 8 x^{3}) \div (2 x - 3)$ $(x - 14 x^{2} + 8 x^{3}) \div (2 x - 3)$
$(6 + 7 y + 6 y^{2}) \div (2 y + 1)$ $(6 + 7 y + 6 y^{2}) \div (2 y + 1)$
$(4 Z^{2} - 5 Z - 7) \div (4 Z + 3)$ $(4 Z^{2} - 5 Z - 7) \div (4 Z + 3)$
$(6 x^{2} - 5 x - 9) \div (- 4 + 3 x)$ $(6 x^{2} - 5 x - 9) \div (- 4 + 3 x)$
$\frac{x^{3} + 3 x^{2} - 4 x - 12}{x + 2}$ $\frac{x^{3} + 3 x^{2} - 4 x - 12}{x + 2}$
$\frac{3 x^{3} + 19 x^{2} + 13 x - 20}{3 x - 2}$ $\frac{3 x^{3} + 19 x^{2} + 13 x - 20}{3 x - 2}$
$\frac{2 a^{4} + 4 a^{2} - 16}{a^{2} - 2}$ $\frac{2 a^{4} + 4 a^{2} - 16}{a^{2} - 2}$
$\frac{6 T^{3} + T^{2} + 2}{3 T^{2} - T + 2}$ $\frac{6 T^{3} + T^{2} + 2}{3 T^{2} - T + 2}$
$\frac{y^{3} + 27}{y + 3}$ $\frac{y^{3} + 27}{y + 3}$
$\frac{D^{3} - 1}{D - 1}$ $\frac{D^{3} - 1}{D - 1}$
$\frac{x^{2} - 2 x y + y^{2}}{x - y}$ $\frac{x^{2} - 2 x y + y^{2}}{x - y}$
$\frac{3 r^{2} - 5 r R + 2 R^{2}}{r - 3 R}$ $\frac{3 r^{2} - 5 r R + 2 R^{2}}{r - 3 R}$
$\frac{t^{3} - 8}{t^{2} + 2 t + 4}$ $\frac{t^{3} - 8}{t^{2} + 2 t + 4}$
$\frac{a^{4} + b^{4}}{a^{2} - 2 a b + 2 b^{2}}$ $\frac{a^{4} + b^{4}}{a^{2} - 2 a b + 2 b^{2}}$

In Exercises 45–56, solve the given problems.

When $2 x^{2} - 9 x - 5$ $2 x^{2} - 9 x - 5$ is divided by $x + c,$ $x + c,$ the quotient is $2 x + 1.$ $2 x + 1.$ Find c.
When $6 x^{2} - x + k$ $6 x^{2} - x + k$ is divided by $3 x + 4,$ $3 x + 4,$ the remainder is zero. Find k.
By division show that $\frac{x^{4} + 1}{x + 1}$ $\frac{x^{4} + 1}{x + 1}$ is not equal to $x^{3} .$ $x^{3} .$
By division show that $\frac{x^{3} + y^{3}}{x + y}$ $\frac{x^{3} + y^{3}}{x + y}$ is not equal to $x^{2} + y^{2} .$ $x^{2} + y^{2} .$
If a gas under constant pressure has volume $V_{1}$ $V_{1}$ at temperature $T_{1}$ $T_{1}$ (in kelvin), then the new volume $V_{2}$ $V_{2}$ when the temperature changes from $T_{1}$ $T_{1}$ to $T_{2}$ $T_{2}$ is given by $V_{2} = V_{1} (1 + \frac{T_{2} - T_{1}}{T_{1}}) .$ $V_{2} = V_{1} (1 + \frac{T_{2} - T_{1}}{T_{1}}) .$ Simplify the right-hand side of this equation.
The area of a certain rectangle can be represented by $6 x^{2} + 19 x + 10.$ $6 x^{2} + 19 x + 10.$ If the length is $2 x + 5,$ $2 x + 5,$ what is the width? (Divide the area by the length.)
In the optical theory dealing with lasers, the following expression arises: $\frac{8 A^{5} + 4 A^{3} μ^{2} E^{2} - A μ^{4} E^{4}}{8 A^{4}} .$ $\frac{8 A^{5} + 4 A^{3} μ^{2} E^{2} - A μ^{4} E^{4}}{8 A^{4}} .$ ( $μ$ $μ$ is the Greek letter mu.) Simplify this expression.
In finding the total resistance of the resistors shown in Fig. 1.14, the following expression is used.

Fig. 1.14

$\frac{6 R_{1} + 6 R_{2} + R_{1} R_{2}}{6 R_{1} R_{2}}$ $\frac{6 R_{1} + 6 R_{2} + R_{1} R_{2}}{6 R_{1} R_{2}}$

Simplify this expression.
When analyzing the potential energy associated with gravitational forces, the expression $\frac{G M m [(R + r) - (R - r)]}{2 r R}$ $\frac{G M m [(R + r) - (R - r)]}{2 r R}$ arises. Simplify this expression.
A computer model shows that the temperature change T in a certain freezing unit is found by using the expression $\frac{3 T^{3} - 8 T^{2} + 8}{T - 2} .$ $\frac{3 T^{3} - 8 T^{2} + 8}{T - 2} .$ Perform the indicated division.
In analyzing the displacement of a certain valve, the expression $\frac{s^{2} - 2 s - 2}{s^{4} + 4}$ $\frac{s^{2} - 2 s - 2}{s^{4} + 4}$ is used. Find the reciprocal of this expression and then perform the indicated division.
In analyzing a rectangular computer image, the area and width of the image vary with time such that the length is given by the expression $\frac{2 t^{3} + 94 t^{2} - 290 t + 500}{2 t + 100} .$ $\frac{2 t^{3} + 94 t^{2} - 290 t + 500}{2 t + 100} .$ By performing the indicated division, find the expression for the length.

Answers to Practice Exercises

$2 x - 3 a$ $2 x - 3 a$
$2 x + 3$ $2 x + 3$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 1.9 Division of Algebraic Expressions

Create new playlist

Sign In

Sign Up

Table of Contents for
1.9 Division of Algebraic Expressions