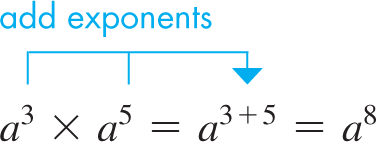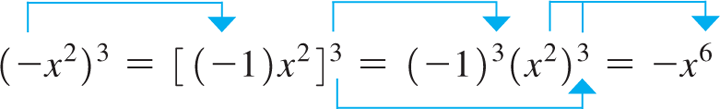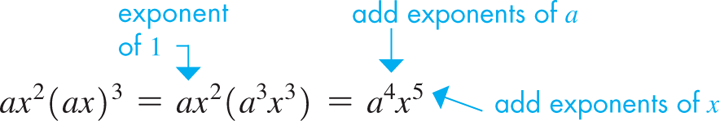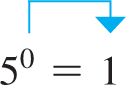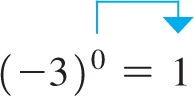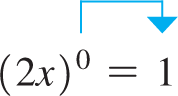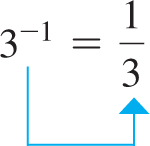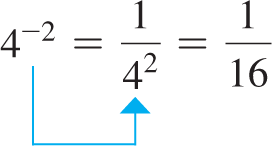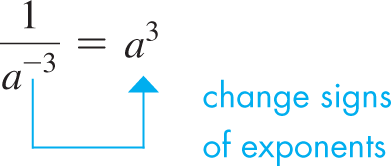Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1.4 Exponents and Unit Conversions

Positive Integer Exponents • Zero and Negative Exponents • Order of Operations • Evaluating Algebraic Expressions • Converting Units

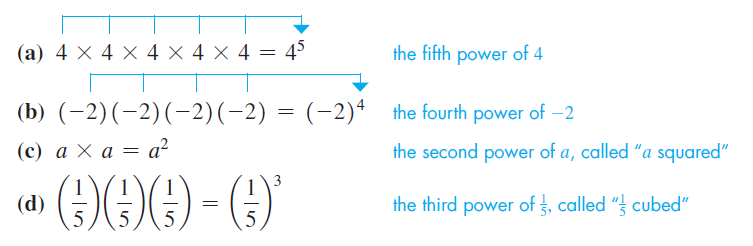
In mathematics and its applications, we often have a number multiplied by itself several times. To show this type of product, we use the notation $a^{n},$ $a^{n},$ where a is the number and n is the number of times it appears. In the expression $a^{n},$ $a^{n},$ the number a is called the base, and n is called the exponent; in words, $a^{n}$ $a^{n}$ is read as “the nth power of a.”

EXAMPLE 1 Meaning of exponents

Meaning of exponents are explained in four steps.

.4-3 Full Alternative Text

We now state the basic operations with exponents using positive integers as exponents. Therefore, with m and n as positive integers, we have the following operations:

a^{m} \times a^{n} = a^{m + n}

$a^{m} \times a^{n} = a^{m + n}$ (1.3)

\frac{a^{m}}{a^{n}} = a^{m - n} (m > n, a \neq 0) \frac{a^{m}}{a^{n}} = \frac{1}{a^{n - m}} (m < n, a \neq 0)

$\frac{a^{m}}{a^{n}} = a^{m - n} (m > n, a \neq 0) \frac{a^{m}}{a^{n}} = \frac{1}{a^{n - m}} (m < n, a \neq 0)$ (1.4)

{(a^{m})}^{n} = a^{m n}

${(a^{m})}^{n} = a^{m n}$ (1.5)

{(a b)}^{n} = a^{n} b^{n} {(\frac{a}{b})}^{n} = \frac{a^{n}}{b^{n}} (b \neq 0)

${(a b)}^{n} = a^{n} b^{n} {(\frac{a}{b})}^{n} = \frac{a^{n}}{b^{n}} (b \neq 0)$ (1.6)

EXAMPLE 2 Illustrating Eqs. (1.3) and (1.4)

Using Eq. (1.3):	Using the meaning of exponents:
	.4-3 Full Alternative Text
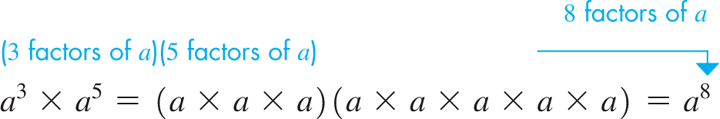Using first form Eq. (1.4):	Using the meaning of exponents:
	$\frac{a^{5}}{a^{3}} = \frac{\overset{1}{a} \times \overset{1}{a} \times \overset{1}{a} \times a \times a}{\underset{1}{a} \times \underset{1}{a} \times \underset{1}{a}} = a^{2}$ $\frac{a^{5}}{a^{3}} = \frac{\overset{1}{a} \times \overset{1}{a} \times \overset{1}{a} \times a \times a}{\underset{1}{a} \times \underset{1}{a} \times \underset{1}{a}} = a^{2}$
Using second form Eq. (1.4):	Using the meaning of exponents:
.4-3 Full Alternative Text	$\frac{a^{3}}{a^{5}} = \frac{\overset{1}{a} \times \overset{1}{a} \times \overset{1}{a}}{\underset{1}{a} \times \underset{1}{a} \times \underset{1}{a} \times a \times a} = \frac{1}{a^{2}}$ $\frac{a^{3}}{a^{5}} = \frac{\overset{1}{a} \times \overset{1}{a} \times \overset{1}{a}}{\underset{1}{a} \times \underset{1}{a} \times \underset{1}{a} \times a \times a} = \frac{1}{a^{2}}$

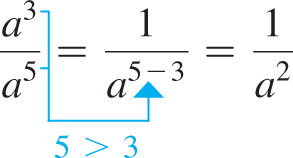EXAMPLE 3 Illustrating Eqs. (1.5) and (1.6)

Using Eq. (1.5):	Using the meaning of exponents:
	${(a^{5})}^{3} = (a^{5}) (a^{5}) (a^{5}) = a^{5 + 5 + 5} = a^{15}$ ${(a^{5})}^{3} = (a^{5}) (a^{5}) (a^{5}) = a^{5 + 5 + 5} = a^{15}$
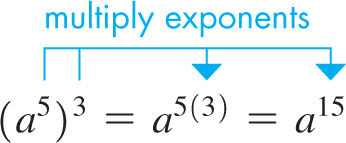Using first form Eq. (1.6):	Using the meaning of exponents:
	${(a b)}^{3} = (a b) (a b) (a b) = a^{3} b^{3}$ ${(a b)}^{3} = (a b) (a b) (a b) = a^{3} b^{3}$
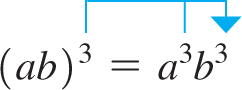Using second form Eq. (1.6):	Using the meaning of exponents:
	${(\frac{a}{b})}^{3} = (\frac{a}{b}) (\frac{a}{b}) (\frac{a}{b}) = \frac{a^{3}}{b^{3}}$ ${(\frac{a}{b})}^{3} = (\frac{a}{b}) (\frac{a}{b}) (\frac{a}{b}) = \frac{a^{3}}{b^{3}}$

CAUTION

When an expression involves a product or a quotient of different bases, only exponents of the same base may be combined. Consider the following example.

CAUTION

In illustration (b), note that $a x^{2}$ $a x^{2}$ means a times the square of x and does not mean $a^{2} x^{2},$ $a^{2} x^{2},$ whereas ${(a x)}^{3}$ ${(a x)}^{3}$ does mean $a^{3} x^{3} .$ $a^{3} x^{3} .$

EXAMPLE 4 Other illustrations of exponents

.4-3 Full Alternative Text
.4-3 Full Alternative Text
$\frac{{(3 \times 2)}^{4}}{{(3 \times 5)}^{3}} = \frac{3^{4} 2^{4}}{3^{3} 5^{3}} = \frac{3 \times 2^{4}}{5^{3}}$ $\frac{{(3 \times 2)}^{4}}{{(3 \times 5)}^{3}} = \frac{3^{4} 2^{4}}{3^{3} 5^{3}} = \frac{3 \times 2^{4}}{5^{3}}$
$\frac{{(r y^{3})}^{2}}{r {(y^{2})}^{4}} = \frac{r^{2} y^{6}}{r y^{8}} = \frac{r}{y^{2}}$ $\frac{{(r y^{3})}^{2}}{r {(y^{2})}^{4}} = \frac{r^{2} y^{6}}{r y^{8}} = \frac{r}{y^{2}}$

EXAMPLE 5 Exponents—beam deflection

In analyzing the amount a beam bends, the following simplification may be used. (P is the force applied to a beam of length L; E and I are constants related to the beam.)

\begin{array}{rcl} \frac{1}{2} (\frac{P L}{4 E I}) (\frac{2}{3}) {(\frac{L}{2})}^{2} & = & \frac{1}{2} (\frac{P L}{4 E I}) (\frac{2}{3}) (\frac{L^{2}}{2^{2}}) \\ = & \frac{\overset{1}{2} P L (L^{2})}{\underset{1}{2} (3) (4) (4) E I} = \frac{P L^{3}}{48 E I} \end{array}

$\begin{array}{rcl} \frac{1}{2} (\frac{P L}{4 E I}) (\frac{2}{3}) {(\frac{L}{2})}^{2} & = & \frac{1}{2} (\frac{P L}{4 E I}) (\frac{2}{3}) (\frac{L^{2}}{2^{2}}) \\ = & \frac{\overset{1}{2} P L (L^{2})}{\underset{1}{2} (3) (4) (4) E I} = \frac{P L^{3}}{48 E I} \end{array}$

In simplifying this expression, we combined exponents of L and divided out the 2 that was a factor common to the numerator and the denominator.

ZERO AND NEGATIVE EXPONENTS

If $n = m$ $n = m$ in Eqs. (1.4), we have $a^{m} / a^{m} = a^{m - m} = a^{0} .$ $a^{m} / a^{m} = a^{m - m} = a^{0} .$ Also, $a^{m} / a^{m} = 1,$ $a^{m} / a^{m} = 1,$ since any nonzero quantity divided by itself equals 1. Therefore, for Eqs. (1.4) to hold for $m = n,$ $m = n,$

a^{0} = 1 (a \neq 0)

$a^{0} = 1 (a \neq 0)$ (1.7)

Equation (1.7) states that any nonzero expression raised to the zero power is 1. Zero exponents can be used with any of the operations for exponents.

EXAMPLE 6 Zero as an exponent

We note in illustration (g) that only t is raised to the zero power. If the quantity 2t were raised to the zero power, it would be written as ${(2 t)}^{0},$ ${(2 t)}^{0},$ as in part (d).

Applying both forms of Eq. (1.4) to the case where $n > m$ $n > m$ leads to the definition of a negative exponent. For example, applying both forms to $a^{2} / a^{7},$ $a^{2} / a^{7},$ we have

\frac{a^{2}}{a^{7}} = a^{2 - 7} = a^{- 5} and \frac{a^{2}}{a^{7}} = \frac{1}{a^{7 - 2}} = \frac{1}{a^{5}}

$\frac{a^{2}}{a^{7}} = a^{2 - 7} = a^{- 5} and \frac{a^{2}}{a^{7}} = \frac{1}{a^{7 - 2}} = \frac{1}{a^{5}}$

For these results to be equal, then $a^{- 5} = 1 / a^{5} .$ $a^{- 5} = 1 / a^{5} .$ Thus, if we define

a^{- n} = \frac{1}{a^{n}} (a \neq 0)

$a^{- n} = \frac{1}{a^{n}} (a \neq 0)$ (1.8)

then all the laws of exponents will hold for negative integers.

EXAMPLE 7 Negative exponents

$An expression with negative exponent. 4 to the power of negative 2 equals, start fraction 1 over 4 squared end fraction equal 1 sixteenth.$
$An expression with negative exponent. start fraction 1 over a to the power of negative 3 end fraction equals a to the power of 3. A text points from the negative 3 exponent to the cubed exponent and states, change signs f exponents.$
${(3 x)}^{- 1} = \frac{1}{3 x}$ ${(3 x)}^{- 1} = \frac{1}{3 x}$
$3 x^{- 1} = 3 (\frac{1}{x}) = \frac{3}{x}$ $3 x^{- 1} = 3 (\frac{1}{x}) = \frac{3}{x}$
${(\frac{a^{3}}{x})}^{- 2} = \frac{{(a^{3})}^{- 2}}{x^{- 2}} = \frac{a^{- 6}}{x^{- 2}} = \frac{x^{2}}{a^{6}}$ ${(\frac{a^{3}}{x})}^{- 2} = \frac{{(a^{3})}^{- 2}}{x^{- 2}} = \frac{a^{- 6}}{x^{- 2}} = \frac{x^{2}}{a^{6}}$

ORDER OF OPERATIONS

We have seen that the basic operations on numbers must be performed in a particular order. Since raising a number to a power is actually multiplication, it is performed before additions and subtractions, and in fact, before multiplications and divisions.

EXAMPLE 8 Using order of operations

$\begin{array}{l} \begin{array}{rcl} 8 - {(- 1)}^{2} - 2 {(- 3)}^{2} & = & 8 - 1 - 2 (9) \\ = & 8 - 1 - 18 = - 11 \end{array} & \begin{array}{l} apply exponents first, \\ then multiply, and then \\ subtract \end{array} \end{array}$ $\begin{array}{l} \begin{array}{rcl} 8 - {(- 1)}^{2} - 2 {(- 3)}^{2} & = & 8 - 1 - 2 (9) \\ = & 8 - 1 - 18 = - 11 \end{array} & \begin{array}{l} apply exponents first, \\ then multiply, and then \\ subtract \end{array} \end{array}$
$\begin{array}{l} \begin{array}{rcl} 806 \div {(26.1 - 9.09)}^{2} & = & 806 \div {(\underline{17.0} 1)}^{2} \\ = & 806 \div \underline{289} .3401 = 2.79 \end{array} & \begin{array}{l} subtract inside parentheses \\ first, then square the answer, \\ and then divide \end{array} \end{array}$ $\begin{array}{l} \begin{array}{rcl} 806 \div {(26.1 - 9.09)}^{2} & = & 806 \div {(\underline{17.0} 1)}^{2} \\ = & 806 \div \underline{289} .3401 = 2.79 \end{array} & \begin{array}{l} subtract inside parentheses \\ first, then square the answer, \\ and then divide \end{array} \end{array}$

NOTE

[In part (b), the significant digits retained from each intermediate step are underlined.]

EXAMPLE 9 Even and odd powers

Using the meaning of a power of a number, we have

\begin{array}{l} {(- 2)}^{2} = (- 2) (- 2) = 4 {(- 2)}^{3} = (- 2) (- 2) (- 2) = - 8 \\ {(- 2)}^{4} = 16 {(- 2)}^{5} = - 32 {(- 2)}^{6} = 64 {(- 2)}^{7} = - 128 \end{array}

$\begin{array}{l} {(- 2)}^{2} = (- 2) (- 2) = 4 {(- 2)}^{3} = (- 2) (- 2) (- 2) = - 8 \\ {(- 2)}^{4} = 16 {(- 2)}^{5} = - 32 {(- 2)}^{6} = 64 {(- 2)}^{7} = - 128 \end{array}$

NOTE

[Note that a negative number raised to an even power gives a positive value, and a negative number raised to an odd power gives a negative value.]

EVALUATING ALGEBRAIC EXPRESSIONS

An algebraic expression is evaluated by substituting given values of the literal numbers in the expression and calculating the result. On a calculator, the key is used to square numbers, and the or key is used for other powers.

To calculate the value of $20 \times 6 + 200/5 - 3^{4},$ $20 \times 6 + 200/5 - 3^{4},$ we use the key sequence

20 times 6 + 200 divided by 5 minus 3 caret 4.

with the result of 79 shown in the display of Fig. 1.9. Note that calculators are programmed to follow the correct order of operations.

A calculator screen with input 20 times 6 plus 200 divided by 5 minus 3 raised to the fourth, and output 79. — Fig. 1.9

EXAMPLE 10 Evaluating an expression—free-fall distance

The distance (in ft) that an object falls in 4.2 s is found by substituting 4.2 for t in the expression $16.0 t^{2}$ $16.0 t^{2}$ as shown below:

16.0 {(4.2)}^{2} = 280 ft

$16.0 {(4.2)}^{2} = 280 ft$

The calculator result from the first line of Fig. 1.10 has been rounded off to two significant digits, the accuracy of 4.2.

A calculator screen with input 16 times 4.2 squared, and output 282.24; input 8.380 plus 0.0115 times, negative 2.87, cubed, and output 8.108141116. — Fig. 1.10

EXAMPLE 11 Evaluating an expression—length of a wire

A wire made of a special alloy has a length L (in m) given by $L = a + 0.0115 T^{3},$ $L = a + 0.0115 T^{3},$ where T (in $° C$ $° C$ ) is the temperature (between $- 4 ° C$ $- 4 ° C$ and $4 ° C$ $4 ° C$ ). To find the wire length for L for $a = 8.380 m$ $a = 8.380 m$ and $T = - 2.87 ° C,$ $T = - 2.87 ° C,$ we substitute these values to get

L = 8.380 + 0.0115 {(- 2.87)}^{3} = 8.108 m

$L = 8.380 + 0.0115 {(- 2.87)}^{3} = 8.108 m$

The calculator result from the second line of Fig. 1.10 has been rounded to the nearest thousandth.

OPERATIONS WITH UNITS AND UNIT CONVERSIONS

Many problems in science and technology require us to perform operations on numbers with units. For multiplication, division, powers, or roots, whatever operation is performed on the numbers also is performed on the units. For addition and subtraction, only numbers with the same units can be combined, and the answer will have the same units as the numbers in the problem. Essentially, units are treated the same as any other algebraic symbol.

EXAMPLE 12 Algebraic operations with units

$(2 ft) (4 lb) = 8 ft \cdot lb the dot symbol represents multiplication$ $(2 ft) (4 lb) = 8 ft \cdot lb the dot symbol represents multiplication$
$255 m + 121 m = 376 m note that the units are not added$ $255 m + 121 m = 376 m note that the units are not added$
${(3.45 in .)}^{2} = 11.9 in .^{2} the unit is squared as well as the number$ ${(3.45 in .)}^{2} = 11.9 in .^{2} the unit is squared as well as the number$
$(65.0 \frac{mi}{h}) (3.52 h) = 229 mi note that \frac{mi}{h} \times \frac{h}{1} = \frac{mi}{1} = mi$ $(65.0 \frac{mi}{h}) (3.52 h) = 229 mi note that \frac{mi}{h} \times \frac{h}{1} = \frac{mi}{1} = mi$
$\frac{8.48 g}{{(1.69 m)}^{3}} = \frac{8.48 g}{{(1.69)}^{3} m^{3}} = 1.76 g / m^{3} the units are divided$ $\frac{8.48 g}{{(1.69 m)}^{3}} = \frac{8.48 g}{{(1.69)}^{3} m^{3}} = 1.76 g / m^{3} the units are divided$
$\begin{array}{rcl} (\frac{8.75 mi}{1.32 {min}^{2}}) {(\frac{1 min}{60 s})}^{2} (\frac{5280 ft}{1 mi}) & = & \frac{(8.75 mi) (1 {min}^{2}) (5280 ft)}{(1.32 {min}^{2}) (3600 s^{2}) (1 mi)} \begin{array}{l} {the units min}^{2} \\ and mi both \end{array} \\ cancel \\ = & 9.72 ft / s^{2} \end{array}$ $\begin{array}{rcl} (\frac{8.75 mi}{1.32 {min}^{2}}) {(\frac{1 min}{60 s})}^{2} (\frac{5280 ft}{1 mi}) & = & \frac{(8.75 mi) (1 {min}^{2}) (5280 ft)}{(1.32 {min}^{2}) (3600 s^{2}) (1 mi)} \begin{array}{l} {the units min}^{2} \\ and mi both \end{array} \\ cancel \\ = & 9.72 ft / s^{2} \end{array}$

Often, it is necessary to convert from one set of units to another. This can be accomplished by using conversion factors (for example, $1 in . = 2.54 cm$ $1 in . = 2.54 cm$ ). Several useful conversion factors are shown in Table 1.1.

Table 1.1 Conversion Factors

Length	Volume/Capacity	Weight/Mass	Energy/Power
$1 in . = 2.54 cm$ $1 in . = 2.54 cm$ (exact)	${1 ft}^{3} = 28.32 L$ ${1 ft}^{3} = 28.32 L$	$1 lb = 453.6 g$ $1 lb = 453.6 g$	$1 Btu = 778.2 ft \cdot lb$ $1 Btu = 778.2 ft \cdot lb$
$1 ft = 0.3048 m$ $1 ft = 0.3048 m$ (exact)	$1 L = 1.057 qt$ $1 L = 1.057 qt$	$1 kg = 2.205 lb$ $1 kg = 2.205 lb$	$1 ft \cdot lb = 1.356 J$ $1 ft \cdot lb = 1.356 J$
$1 km = 0.6214 mi$ $1 km = 0.6214 mi$	$1 gal = 3.785 L$ $1 gal = 3.785 L$	$1 lb = 4.448 N$ $1 lb = 4.448 N$	$1 hp = 550 ft \cdot lb / s$ $1 hp = 550 ft \cdot lb / s$ (exact)
$1 mi = 5280 ft$ $1 mi = 5280 ft$ (exact)			$1 hp = 746.0 W$ $1 hp = 746.0 W$

Metric prefixes are sometimes attached to units to indicate they are multiplied by a given power of ten. Table 1.2 (on the next page) shows some commonly used prefixes.

Table 1.2 Metric Prefixes

Prefix	Factor	Symbol
exa	$10^{18}$ $10^{18}$	E
peta	$10^{15}$ $10^{15}$	P
tera	$10^{12}$ $10^{12}$	T
giga	$10^{9}$ $10^{9}$	G
mega	$10^{6}$ $10^{6}$	M
kilo	$10^{3}$ $10^{3}$	k
hecto	$10^{2}$ $10^{2}$	h
deca	$10^{1}$ $10^{1}$	da
deci	$10^{- 1}$ $10^{- 1}$	d
centi	$10^{- 2}$ $10^{- 2}$	c
milli	$10^{- 3}$ $10^{- 3}$	m
micro	$10^{- 6}$ $10^{- 6}$	$μ$ $μ$
nano	$10^{- 9}$ $10^{- 9}$	n
pico	$10^{- 12}$ $10^{- 12}$	p
femto	$10^{- 15}$ $10^{- 15}$	f
atto	$10^{- 18}$ $10^{- 18}$	a

When a conversion factor is written in fractional form, the fraction has a value of 1 since the numerator and denominator represent the same quantity. For example, $\frac{1 in .}{2.54 cm} = 1$ $\frac{1 in .}{2.54 cm} = 1$ or $\frac{1 km}{1000 m} = 1.$ $\frac{1 km}{1000 m} = 1.$ To convert units, we multiply the given number (including its units) by one or more of these fractions placed in such a way that the units we wish to eliminate will cancel and the units we wish to retain will remain in the answer. Since we are multiplying the given number by fractions that have a value of 1, the original quantity remains unchanged even though it will be expressed in different units.

EXAMPLE 13 Converting units

The length of a certain smartphone is 13.8 cm. Convert this to inches.

$\begin{matrix} 13.8 cm = \underset{|}{\underset{⎵}{\frac{13.8 cm}{1}}} \times \underset{|}{\underset{⎵}{\frac{1 in .}{2.54 cm}}} = \frac{(13.8) (1) in .}{(1) (2.54)} = 5.43 in . \\ original number 1 \end{matrix}$ $\begin{matrix} 13.8 cm = \underset{|}{\underset{⎵}{\frac{13.8 cm}{1}}} \times \underset{|}{\underset{⎵}{\frac{1 in .}{2.54 cm}}} = \frac{(13.8) (1) in .}{(1) (2.54)} = 5.43 in . \\ original number 1 \end{matrix}$

Notice that the unit cm appears in both the numerator and denominator and therefore cancels, leaving only the unit inches in the final answer.
A car is traveling at 65.0 mi/h. Convert this speed to km/min (kilometers per minute).

From Table 1.1, we note that $1 km = 0.6214 mi,$ $1 km = 0.6214 mi,$ and we know that $1 h = 60 min .$ $1 h = 60 min .$ Using these values, we have

$\begin{array}{rcl} 65.0 \frac{mi}{h} & = & \frac{65.0 mi}{1 h} \times \frac{1 km}{0.6214 mi} \times \frac{1 h}{60 min} = \frac{(65.0) (1) (1) km}{(1) (0.6214) (60) min} \\ = & 1.74 km / min \end{array}$ $\begin{array}{rcl} 65.0 \frac{mi}{h} & = & \frac{65.0 mi}{1 h} \times \frac{1 km}{0.6214 mi} \times \frac{1 h}{60 min} = \frac{(65.0) (1) (1) km}{(1) (0.6214) (60) min} \\ = & 1.74 km / min \end{array}$

We note that the units mi and h appear in both numerator and denominator and therefore cancel out, leaving the units km and min. Also note that the 1’s and 60 are exact.

See Appendix B for a description of the U.S. Customary and SI units, as well as a list of all the units used in this text and their symbols.
The density of iron is $7.86 g / {cm}^{3}$ $7.86 g / {cm}^{3}$ (grams per cubic centimeter). Express this density in $kg / m^{3}$ $kg / m^{3}$ (kilograms per cubic meter).

From Table 1.2, $1 kg = 1000 g$ $1 kg = 1000 g$ exactly, and $1 cm = 0.01 m$ $1 cm = 0.01 m$ exactly. Therefore,

$\begin{array}{rcl} 7.86 \frac{g}{{cm}^{3}} & = & \frac{7.86 g}{1 {cm}^{3}} \times \frac{1 kg}{1000 g} \times {(\frac{1 cm}{0.01 m})}^{3} = \frac{(7.86) (1) (1^{3}) kg}{(1) (1000) ({0.01}^{3}) m^{3}} \\ = & \frac{(7.86) kg}{0.001 m^{3}} = 7860 kg / m^{3} \end{array}$ $\begin{array}{rcl} 7.86 \frac{g}{{cm}^{3}} & = & \frac{7.86 g}{1 {cm}^{3}} \times \frac{1 kg}{1000 g} \times {(\frac{1 cm}{0.01 m})}^{3} = \frac{(7.86) (1) (1^{3}) kg}{(1) (1000) ({0.01}^{3}) m^{3}} \\ = & \frac{(7.86) kg}{0.001 m^{3}} = 7860 kg / m^{3} \end{array}$

Here, the units g and ${cm}^{3}$ ${cm}^{3}$ are in both numerator and denominator and therefore cancel out, leaving units of kg and $m^{3} .$ $m^{3} .$ Also, all numbers are exact, except 7.86.

EXERCISES 1.4

In Exercises 1 and 2, make the given changes in the indicated examples of this section, and then simplify the resulting expression.

In Example 4(a), change ${(- x^{2})}^{3}$ ${(- x^{2})}^{3}$ to ${(- x^{3})}^{2} .$ ${(- x^{3})}^{2} .$
In Example 6(d), change ${(2 x)}^{0}$ ${(2 x)}^{0}$ to $2 x^{0} .$ $2 x^{0} .$

In Exercises 3–42, simplify the given expressions. Express results with positive exponents only.

$x^{3} x^{4}$ $x^{3} x^{4}$
$y^{2} y^{7}$ $y^{2} y^{7}$
$2 b^{4} b^{2}$ $2 b^{4} b^{2}$
$3 k^{5} k$ $3 k^{5} k$
$\frac{m^{5}}{m^{3}}$ $\frac{m^{5}}{m^{3}}$
$\frac{2 x^{6}}{- x}$ $\frac{2 x^{6}}{- x}$
$\frac{- n^{5}}{7 n^{9}}$ $\frac{- n^{5}}{7 n^{9}}$
$\frac{3 s}{s^{4}}$ $\frac{3 s}{s^{4}}$
${(P^{2})}^{4}$ ${(P^{2})}^{4}$
${(x^{8})}^{3}$ ${(x^{8})}^{3}$
${(a T^{2})}^{30}$ ${(a T^{2})}^{30}$
${(3 r^{2})}^{3}$ ${(3 r^{2})}^{3}$
${(\frac{2}{b})}^{3}$ ${(\frac{2}{b})}^{3}$
${(\frac{F}{t})}^{20}$ ${(\frac{F}{t})}^{20}$
${(\frac{x^{2}}{- 2})}^{4}$ ${(\frac{x^{2}}{- 2})}^{4}$
${(\frac{3}{n^{3}})}^{3}$ ${(\frac{3}{n^{3}})}^{3}$
${(8 a)}^{0}$ ${(8 a)}^{0}$
$- v^{0}$ $- v^{0}$
$- 3 x^{0}$ $- 3 x^{0}$
$- {(- 2)}^{0}$ $- {(- 2)}^{0}$
$6^{- 1}$ $6^{- 1}$
$- w^{- 5}$ $- w^{- 5}$
$\frac{1}{R^{- 2}}$ $\frac{1}{R^{- 2}}$
$\frac{1}{- t^{- 48}}$ $\frac{1}{- t^{- 48}}$
${(- t^{2})}^{7}$ ${(- t^{2})}^{7}$
${(- y^{3})}^{5}$ ${(- y^{3})}^{5}$
$- \frac{L^{- 3}}{L^{- 5}}$ $- \frac{L^{- 3}}{L^{- 5}}$
$2 i^{40} i^{- 70}$ $2 i^{40} i^{- 70}$
$\frac{2 v^{4}}{{(2 v)}^{4}}$ $\frac{2 v^{4}}{{(2 v)}^{4}}$
$\frac{x^{2} x^{3}}{{(x^{2})}^{3}}$ $\frac{x^{2} x^{3}}{{(x^{2})}^{3}}$
$\frac{{(n^{2})}^{4}}{{(n^{4})}^{2}}$ $\frac{{(n^{2})}^{4}}{{(n^{4})}^{2}}$
$\frac{{(3 t)}^{- 1}}{- 3 t^{- 1}}$ $\frac{{(3 t)}^{- 1}}{- 3 t^{- 1}}$
${(π^{0} x^{2} a^{- 1})}^{- 1}$ ${(π^{0} x^{2} a^{- 1})}^{- 1}$
${(3 m^{- 2} n^{4})}^{- 2}$ ${(3 m^{- 2} n^{4})}^{- 2}$
${(- 8 g^{- 1} s^{3})}^{2}$ ${(- 8 g^{- 1} s^{3})}^{2}$
$a x^{- 2} {(- a^{2} x)}^{3}$ $a x^{- 2} {(- a^{2} x)}^{3}$
${(\frac{4 x^{- 1}}{a^{- 1}})}^{- 3}$ ${(\frac{4 x^{- 1}}{a^{- 1}})}^{- 3}$
${(\frac{2 b^{2}}{- y^{5}})}^{- 2}$ ${(\frac{2 b^{2}}{- y^{5}})}^{- 2}$
$\frac{15 n^{2} T^{5}}{3 n^{- 1} T^{6}}$ $\frac{15 n^{2} T^{5}}{3 n^{- 1} T^{6}}$
$\frac{{(n R T^{- 2})}^{32}}{R^{- 2} T^{32}}$ $\frac{{(n R T^{- 2})}^{32}}{R^{- 2} T^{32}}$

In Exercises 43–50, evaluate the given expressions. In Exercises 45–50, all numbers are approximate.

$7 (- 4) - {(- 5)}^{2}$ $7 (- 4) - {(- 5)}^{2}$
$6 - | - 2 |^{5} - (- 2) (8)$ $6 - | - 2 |^{5} - (- 2) (8)$
$- {(- 26.5)}^{2} - {(- 9.85)}^{3}$ $- {(- 26.5)}^{2} - {(- 9.85)}^{3}$
$- {0.711}^{2} - {(- | - 0.809 |)}^{6}$ $- {0.711}^{2} - {(- | - 0.809 |)}^{6}$
$\frac{3.07 (- | - 1.86 |)}{{(- 1.86)}^{4} + 1.596}$ $\frac{3.07 (- | - 1.86 |)}{{(- 1.86)}^{4} + 1.596}$
$\frac{{15.66}^{2} - {(- 4.017)}^{4}}{1.044 (- 3.68)}$ $\frac{{15.66}^{2} - {(- 4.017)}^{4}}{1.044 (- 3.68)}$
$2.38 {(- 10.7)}^{2} - \frac{254}{{1.17}^{3}}$ $2.38 {(- 10.7)}^{2} - \frac{254}{{1.17}^{3}}$
$4.2 (2.6) + \frac{0.889}{1.89 - {1.09}^{2}}$ $4.2 (2.6) + \frac{0.889}{1.89 - {1.09}^{2}}$

In Exercises 51–62, perform the indicated operations.

Does ${(\frac{1}{x^{- 1}})}^{- 1}$ ${(\frac{1}{x^{- 1}})}^{- 1}$ represent the reciprocal of x?
Does ${(\frac{0.2 - 5^{- 1}}{10^{- 2}})}^{0}$ ${(\frac{0.2 - 5^{- 1}}{10^{- 2}})}^{0}$ equal 1? Explain.
If $a^{3} = 5,$ $a^{3} = 5,$ then what does $a^{12}$ $a^{12}$ equal?
Is $a^{- 2} < a^{- 1}$ $a^{- 2} < a^{- 1}$ for any negative value of a? Explain.
If a is a positive integer, simplify ${(x^{a} \cdot x^{- a})}^{5} .$ ${(x^{a} \cdot x^{- a})}^{5} .$
If a and b are positive integers, simplify ${(- y^{a - b} \cdot y^{a + b})}^{2} .$ ${(- y^{a - b} \cdot y^{a + b})}^{2} .$
In developing the “big bang” theory of the origin of the universe, the expression ${(k T / (h c))}^{3} {(G k T h c)}^{2} c$ ${(k T / (h c))}^{3} {(G k T h c)}^{2} c$ arises. Simplify this expression.
In studying planetary motion, the expression $(G m M) {(m r)}^{- 1} (r^{- 2})$ $(G m M) {(m r)}^{- 1} (r^{- 2})$ arises. Simplify this expression.
In designing a cam for a fire engine pump, the expression $π {(\frac{r}{2})}^{3} (\frac{4}{3 π r^{2}})$ $π {(\frac{r}{2})}^{3} (\frac{4}{3 π r^{2}})$ is used. Simplify this expression.
For a certain integrated electric circuit, it is necessary to simplify the expression $\frac{g M {(2 π f M)}^{- 2}}{2 π f C} .$ $\frac{g M {(2 π f M)}^{- 2}}{2 π f C} .$ Perform this simplification.
If $2500 is invested at 4.2% interest, compounded quarterly, the amount in the account after 6 years is $2500 {(1 + 0.042/4)}^{24} .$ $2500 {(1 + 0.042/4)}^{24} .$ Calculate this amount (the 1 is exact).
In designing a building, it was determined that the forces acting on an I beam would deflect the beam an amount (in cm), given by $\frac{x (1000 - 20 x^{2} + x^{3})}{1850},$ $\frac{x (1000 - 20 x^{2} + x^{3})}{1850},$ where x is the distance (in m) from one end of the beam. Find the deflection for $x = 6.85 m .$ $x = 6.85 m .$ (The 1000 and 20 are exact.)
Calculate the value of ${(1 + \frac{1}{n})}^{n}$ ${(1 + \frac{1}{n})}^{n}$ for $n = 1, 10, 100, 1000$ $n = 1, 10, 100, 1000$ on a calculator. Round to four decimal places. (For even larger values of n, the value will never exceed 2.7183. The limiting value is a number called e, which will be important in future chapters.)
For computer memory, the metric prefixes have an unusual meaning: $1 KB = 2^{10} bytes, 1 MB = 2^{10} KB, 1 GB = 2^{10} MB,$ $1 KB = 2^{10} bytes, 1 MB = 2^{10} KB, 1 GB = 2^{10} MB,$ and $1 TB = 2^{10} GB .$ $1 TB = 2^{10} GB .$ How many bytes are there in 1 TB? (KB is kilobyte, MB is megabyte, GB is gigabyte, TB is terabyte)

In Exercises 65–68, perform the indicated operations and attach the correct units to your answers.

$(28.2 \frac{ft}{s}) (9.81 s)$ $(28.2 \frac{ft}{s}) (9.81 s)$
$(40.5 \frac{mi}{gal}) (3.7 gal)$ $(40.5 \frac{mi}{gal}) (3.7 gal)$
$(7.25 \frac{m}{s^{2}}) (\frac{1 ft}{0.3048 m}) {(\frac{60 s}{1 min})}^{2}$ $(7.25 \frac{m}{s^{2}}) (\frac{1 ft}{0.3048 m}) {(\frac{60 s}{1 min})}^{2}$
$(238 \frac{kg}{m^{3}}) (\frac{1000 g}{1 kg}) {(\frac{1 m}{100 cm})}^{3}$ $(238 \frac{kg}{m^{3}}) (\frac{1000 g}{1 kg}) {(\frac{1 m}{100 cm})}^{3}$

In Exercises 69–74, make the indicated conversions.

15.7 qt to L
7.50 W to hp
${245 cm}^{2}$ ${245 cm}^{2}$ to ${in.}^{2}$ ${in.}^{2}$
$85.7 {mi}^{2}$ $85.7 {mi}^{2}$ to ${km}^{2}$ ${km}^{2}$
$65.2 \frac{m}{s}$ $65.2 \frac{m}{s}$ to $\frac{ft}{min}$ $\frac{ft}{min}$
$25.0 \frac{mi}{gal}$ $25.0 \frac{mi}{gal}$ to $\frac{km}{L}$ $\frac{km}{L}$

In Exercises 75–82, solve the given problems.

A laptop computer has a screen that measures 15.6 in. across its diagonal. Convert this to centimeters.
GPS satellites orbit the Earth at an altitude of about 12,500 mi. Convert this to kilometers.
A wastewater treatment plant processes 575,000 gal/day. Convert this to liters per hour.
Water flows from a fire hose at a rate of 85 gal/min. Convert this to liters per second.
The speed of sound is about 1130 ft/s. Change this to kilometers per hour.
A military jet flew at a rate of 7200 km/h. What is this speed in meters per second?
At sea level, atmospheric pressure is about $14.7 lb / {in.}^{2} .$ $14.7 lb / {in.}^{2} .$ Express this in pascals (Pa). Hint: A pascal is a $N / m^{2}$ $N / m^{2}$ (see Appendix B).
The density of water is about $62.4 lb / {ft}^{3} .$ $62.4 lb / {ft}^{3} .$ Convert this to kilograms per cubic meter.

Answers to Practice Exercises

$a^{3} x^{5}$ $a^{3} x^{5}$
$\frac{2^{5} c^{3}}{3^{2} d^{2}} = \frac{32 c^{3}}{9 d^{2}}$ $\frac{2^{5} c^{3}}{3^{2} d^{2}} = \frac{32 c^{3}}{9 d^{2}}$
$- 1$ $- 1$
$- c^{3}$ $- c^{3}$
$\frac{a^{2}}{6 x}$ $\frac{a^{2}}{6 x}$
$10.3 lb / {in.}^{2}$ $10.3 lb / {in.}^{2}$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 1.4 Exponents and Unit Conversions

Create new playlist

Sign In

Sign Up

Table of Contents for
1.4 Exponents and Unit Conversions