Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

5.5 Solving Systems of Three Linear Equations in Three Unknowns Algebraically Solving Systems of Three Linear Equations in Three Unknowns Algebraically

5.4 Solving Systems of Two Linear Equations in Two Unknowns by Determinants

Determinant of the Second Order • Cramer’s Rule • Solving Systems of Equations by Determinants

Consider two linear equations in two unknowns, as given in Eqs. (5.4):

\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}

$\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ (5.4)

If we multiply the first of these equations by $b_{2}$ $b_{2}$ and the second by $b_{1},$ $b_{1},$ we obtain

\begin{array}{l} a_{1} b_{2} x + b_{1} b_{2} y = c_{1} b_{2} \\ a_{2} b_{1} x + b_{2} b_{1} y = c_{2} b_{1} \end{array}

$\begin{array}{l} a_{1} b_{2} x + b_{1} b_{2} y = c_{1} b_{2} \\ a_{2} b_{1} x + b_{2} b_{1} y = c_{2} b_{1} \end{array}$ (5.5)

We see that the coefficients of y are the same. Thus, subtracting the second equation from the first, we can solve for x. The solution can be shown to be

x = \frac{c_{1} b_{2} - c_{2} b_{1}}{a_{1} b_{2} - a_{2} b_{1}}

$x = \frac{c_{1} b_{2} - c_{2} b_{1}}{a_{1} b_{2} - a_{2} b_{1}}$ (5.6)

In the same manner, we may show that

y = \frac{a_{1} c_{2} - a_{2} c_{1}}{a_{1} b_{2} - a_{2} b_{1}}

$y = \frac{a_{1} c_{2} - a_{2} c_{1}}{a_{1} b_{2} - a_{2} b_{1}}$ (5.7)

The expression $a_{1} b_{2} - a_{2} b_{1},$ $a_{1} b_{2} - a_{2} b_{1},$ which appears in each of the denominators of Eqs. (5.6) and (5.7), is an example of a special kind of expression called a determinant of the second order. The determinant $a_{1} b_{2} - a_{2} b_{1}$ $a_{1} b_{2} - a_{2} b_{1}$ is denoted by

| \begin{array}{l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array} |

$| \begin{array}{l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array} |$

Therefore, by definition, a determinant of the second order is

| \begin{array}{l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array} | = a_{1} b_{2} - a_{2} b_{1}

$| \begin{array}{l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array} | = a_{1} b_{2} - a_{2} b_{1}$ (5.8)

The numbers $a_{1}$ $a_{1}$ and $b_{1}$ $b_{1}$ are called the elements of the first row of the determinant. The numbers $a_{1}$ $a_{1}$ and $a_{2}$ $a_{2}$ are the elements of the first column of the determinant. In the same manner, the numbers $a_{2}$ $a_{2}$ and $b_{2}$ $b_{2}$ are the elements of the second row, and the numbers $b_{1}$ $b_{1}$ and $b_{2}$ $b_{2}$ are the elements of the second column. The numbers $a_{1}$ $a_{1}$ and $b_{2}$ $b_{2}$ are the elements of the principal diagonal, and the numbers $a_{2}$ $a_{2}$ and $b_{1}$ $b_{1}$ are the elements of the secondary diagonal. Thus, one way of stating the definition indicated in Eq. (5.8) is that the value of a determinant of the second order is found by taking the product of the elements of the principal diagonal and subtracting the product of the elements of the secondary diagonal.

A diagram that is often helpful for remembering the expansion of a second-order determinant is shown in Fig. 5.32.

CAUTION

It is very important in following Eq. (5.8), or the diagram, that you remember to subtract the product $a_{2} b_{1}$ $a_{2} b_{1}$ of the secondary diagonal from the product $a_{1} b_{2}$ $a_{1} b_{2}$ of the principal diagonal.

The following examples illustrate the evaluation of determinants of the second order.

Figure 5.32 Full Alternative Text

EXAMPLE 1 Evaluating a second-order determinant

.4-2 Full Alternative Text

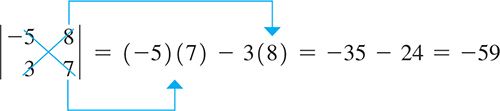
EXAMPLE 2 Evaluating second-order determinants

$| \begin{array}{r} 4 & 6 \\ 3 & 17 \end{array} | = 4 (17) - (3) (6) = 68 - 18 = 50$ $| \begin{array}{r} 4 & 6 \\ 3 & 17 \end{array} | = 4 (17) - (3) (6) = 68 - 18 = 50$
$| \begin{array}{r} 4 & 0 \\ - 3 & 17 \end{array} | = 4 (17) - (- 3) (0) = 68 - 0 = 68$ $| \begin{array}{r} 4 & 0 \\ - 3 & 17 \end{array} | = 4 (17) - (- 3) (0) = 68 - 0 = 68$
$| \begin{array}{r} 3.6 & 6.1 \\ - 3.2 & - 17.2 \end{array} | = 3.6 (- 17.2) - (- 3.2) (6.1) = - 42.4$ $| \begin{array}{r} 3.6 & 6.1 \\ - 3.2 & - 17.2 \end{array} | = 3.6 (- 17.2) - (- 3.2) (6.1) = - 42.4$

Note the signs of the terms being combined.

CAUTION

Be careful. If a diagonal contains a zero, the product is zero.

We note that the numerators and denominators of Eqs. (5.6) and (5.7) may be written as determinants. The numerators of the equations are

| \begin{matrix} c_{1} & b_{1} \\ c_{2} & b_{2} \end{matrix} | and | \begin{matrix} a_{1} & c_{1} \\ a_{2} & c_{2} \end{matrix} |

$| \begin{matrix} c_{1} & b_{1} \\ c_{2} & b_{2} \end{matrix} | and | \begin{matrix} a_{1} & c_{1} \\ a_{2} & c_{2} \end{matrix} |$

Therefore, the solutions for x and y can be expressed directly in terms of determinants, which is called Cramer’s rule.

It is important to notice three key features of the determinants in Cramer’s rule:

The determinants in the denominators are the same and are formed by using the coefficients of x and y.
In the solution for x, the determinant in the numerator is obtained from the determinant in the denominator by replacing the x-coefficients with the constant terms.
In the solution for y, the determinant in the numerator is obtained from the determinant in the denominator by replacing the y-coefficients with the constant terms.

CAUTION

In Using Cramer’s rule, we must be very sure that the equations are written in the form of Eqs. (5.4) before setting up the determinants. That is, be sure the unknowns are in the same order in each equation.

The following examples illustrate the method of solving systems of equations by determinants.

EXAMPLE 3 Solving a system using Cramer’s rule

Solve the following system of equations by determinants:

\begin{array}{rcr} 2 x + y & = & 1 \\ 5 x - 2 y & = & - 11 \end{array}

$\begin{array}{rcr} 2 x + y & = & 1 \\ 5 x - 2 y & = & - 11 \end{array}$

NOTE

[First, note that the equations are in the proper form of Eqs. (5.4) for solution by determinants.]

Next, set up the determinant for the denominator, which consists of the four coefficients in the system, written as shown. It is

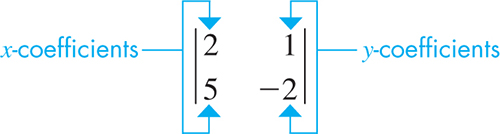
A 2 by 2 determinant matrix with following values. row 1. 2, 1. Row 2. 5, negative 2. Values in first column, 2 and 5 are x coefficients, values in second column, 1 and negative 2 are y coefficients.

For finding x, the determinant in the numerator is obtained from this determinant by replacing the first column by the constants that appear on the right sides of the equations. Thus, the numerator for the solution for x is

A two by two determinant matrix with following values. Row 1. 1, 1. Row 2. negative 11, negative 2. an arrow points to the first column with text that reads Replace x coefficients with the constants.

For finding y, the determinant in the numerator is obtained from the determinant of the denominator by replacing the second column by the constants that appear on the right sides of the equations. Thus, the numerator for the solution for y is

A two by two determinant matrix with following values. Row 1. 2, 1. Row 2. 5, negative 11. Values in second column,1 and negative 11 are y coefficients. Replace that with constants.

Now, set up the solutions for x and y using the determinants above:

\begin{array}{l} x = \frac{| \begin{array}{r} 1 & 1 \\ - 11 & - 2 \end{array} |}{| \begin{array}{r} 2 & 1 \\ 5 & - 2 \end{array} |} = \frac{1 (- 2) - (- 11) (1)}{2 (- 2) - (5) (1)} = \frac{- 2 + 11}{- 4 - 5} = \frac{9}{- 9} = - 1 \\ y = \frac{| \begin{array}{r} 2 & 1 \\ 5 & - 11 \end{array} |}{| \begin{array}{r} 2 & 1 \\ 5 & - 2 \end{array} |} = \frac{2 (- 11) - (5) (1)}{- 9} = \frac{- 22 - 5}{- 9} = 3 \end{array}

$\begin{array}{l} x = \frac{| \begin{array}{r} 1 & 1 \\ - 11 & - 2 \end{array} |}{| \begin{array}{r} 2 & 1 \\ 5 & - 2 \end{array} |} = \frac{1 (- 2) - (- 11) (1)}{2 (- 2) - (5) (1)} = \frac{- 2 + 11}{- 4 - 5} = \frac{9}{- 9} = - 1 \\ y = \frac{| \begin{array}{r} 2 & 1 \\ 5 & - 11 \end{array} |}{| \begin{array}{r} 2 & 1 \\ 5 & - 2 \end{array} |} = \frac{2 (- 11) - (5) (1)}{- 9} = \frac{- 22 - 5}{- 9} = 3 \end{array}$

Therefore, the solution to the system of equations is $x = - 1, y = 3 .$ $x = - 1, y = 3 .$

Substituting these values into the equations, we have

\begin{array}{r} 2 (- 1) + 3 & \underline{\underline{?}} & 1 & and & 5 (- 1) - 2 (3) & \underline{\underline{?}} & - 11 \\ 1 & = & 1 & - 11 & = & - 11 \end{array}

$\begin{array}{r} 2 (- 1) + 3 & \underline{\underline{?}} & 1 & and & 5 (- 1) - 2 (3) & \underline{\underline{?}} & - 11 \\ 1 & = & 1 & - 11 & = & - 11 \end{array}$

which shows that they check.

NOTE

[Because the same determinant appears in each denominator, it needs to be evaluated only once.] This means that three determinants are to be evaluated in order to solve the system.

EXAMPLE 4 Solving a system using Cramer’s rule

Solve the following system of equations by determinants. Numbers are approximate.

\begin{array}{l} 5.3 x + 7.2 y = 4.5 \\ 3.2 x - 6.9 y = 5.7 \end{array}

$\begin{array}{l} 5.3 x + 7.2 y = 4.5 \\ 3.2 x - 6.9 y = 5.7 \end{array}$

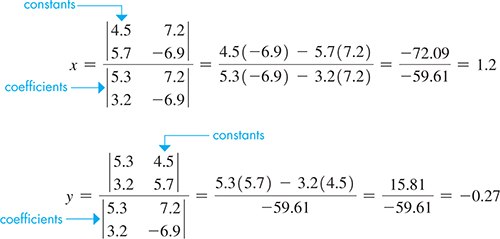
Two equations are solved using Cramer’s rule.

.4-2 Full Alternative Text

It is important to round only the final answers when performing these calculations. When substituted into the original equations, the solutions check reasonably well. The small differences are due to rounding the final answers.

EXAMPLE 5 Solving a system—investment income

Two investments totaling $18,000 yield an annual income of $700. If the first investment has an interest rate of 5.5% and the second a rate of 3.0%, what is the value of each?

Let $x = the$ $x = the$ value of the first investment and $y = the$ $y = the$ value of the second investment. We know that the total of the two investments is $18,000. This leads to the equation $x + y = $18, 000 .$ $x + y = $18, 000 .$ The first investment yields 0.055x dollars annually, and the second yields 0.030y dollars annually. This leads to the equation $0.055 x + 0.030 y = 700 .$ $0.055 x + 0.030 y = 700 .$ These two equations are then solved simultaneously:

\begin{array}{c} \begin{array}{ccccrll} x & + & y & = & 18, 000 & sum of investments \\ 0.055 x & + & 0.030 y & = & 700 & \leftarrow & income \\ ↑ & ↑ \\ 5.5 % value & 3.0 % value \end{array} \end{array} \begin{matrix} x = \end{matrix}

$\begin{array}{c} \begin{array}{ccccrll} x & + & y & = & 18, 000 & sum of investments \\ 0.055 x & + & 0.030 y & = & 700 & \leftarrow & income \\ ↑ & ↑ \\ 5.5 % value & 3.0 % value \end{array} \end{array} \begin{matrix} x = \end{matrix}$

x = \frac{| \begin{matrix} 18, 000 & 1 \\ 700 & 0.030 \end{matrix} |}{| \begin{matrix} 1 & 1 \\ 0.055 & 0.030 \end{matrix} |} = \frac{540 - 700}{0.030 - 0.055} = \frac{- 160}{- 0.025} = 6400

$x = \frac{| \begin{matrix} 18, 000 & 1 \\ 700 & 0.030 \end{matrix} |}{| \begin{matrix} 1 & 1 \\ 0.055 & 0.030 \end{matrix} |} = \frac{540 - 700}{0.030 - 0.055} = \frac{- 160}{- 0.025} = 6400$

The value of y can be found most easily by substituting this value of x into the first equation, $y = 18, 000 - x = 18, 000 - 6400 = 11, 600 .$ $y = 18, 000 - x = 18, 000 - 6400 = 11, 600 .$

Therefore, the values invested are $6400 and $11,600. Checking, the total income is $$6400 (0.055) + $11, 600 (0.030) = $700,$ $$6400 (0.055) + $11, 600 (0.030) = $700,$ which agrees with the statement of the problem.

CAUTION

The equations must be in the form of Eqs. (5.4) before the determinants are set up.

The specific positions of the values in the determinants are based on that form of writing the system. If either unknown is missing from an equation, a zero must be placed in the proper position. Also, from Example 4, we see that determinants are easier to use than other algebraic methods when the coefficients are decimals.

CAUTION

If the determinant of the denominator is zero, we do not have a unique solution because this would require division by zero. If the determinant of the denominator is zero and that of the numerator is not zero, the system is inconsistent. If the determinants of both numerator and denominator are zero, the system is dependent.

Exercises 5.4

In Exercises 1–4, make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 2(a), change the 6 to $- 6$ $- 6$ and then evaluate.
In Example 2(a), change the 4 to $- 4$ $- 4$ and the 6 to $- 6$ $- 6$ and then evaluate.
In Example 3, change the $+$ $+$ to $-$ $-$ in the first equation and then solve the system of equations.
In Example 5, change $700 to $830 and then solve for the values of the investments.

In Exercises 5–18, evaluate the given determinants.

$| \begin{array}{r} 8 & 3 \\ 4 & 1 \end{array} |$ $| \begin{array}{r} 8 & 3 \\ 4 & 1 \end{array} |$
$| \begin{array}{r} - 1 & 3 \\ 2 & 6 \end{array} |$ $| \begin{array}{r} - 1 & 3 \\ 2 & 6 \end{array} |$
$| \begin{array}{r} 3 & - 5 \\ 7 & - 2 \end{array} |$ $| \begin{array}{r} 3 & - 5 \\ 7 & - 2 \end{array} |$
$| \begin{array}{r} - 4 & 7 \\ 1 & - 3 \end{array} |$ $| \begin{array}{r} - 4 & 7 \\ 1 & - 3 \end{array} |$
$| \begin{array}{r} 15 & - 9 \\ 12 & 0 \end{array} |$ $| \begin{array}{r} 15 & - 9 \\ 12 & 0 \end{array} |$
$| \begin{array}{r} - 20 & - 15 \\ - 8 & - 6 \end{array} |$ $| \begin{array}{r} - 20 & - 15 \\ - 8 & - 6 \end{array} |$
$| \begin{array}{r} - 20 & 110 \\ - 70 & - 80 \end{array} |$ $| \begin{array}{r} - 20 & 110 \\ - 70 & - 80 \end{array} |$
$| \begin{array}{r} - 6.5 & 12.2 \\ - 15.5 & 34.6 \end{array} |$ $| \begin{array}{r} - 6.5 & 12.2 \\ - 15.5 & 34.6 \end{array} |$
$| \begin{array}{r} 0.75 & - 1.32 \\ 0.15 & 1.18 \end{array} |$ $| \begin{array}{r} 0.75 & - 1.32 \\ 0.15 & 1.18 \end{array} |$
$| \begin{array}{r} 0.20 & - 0.05 \\ 0.28 & 0.09 \end{array} |$ $| \begin{array}{r} 0.20 & - 0.05 \\ 0.28 & 0.09 \end{array} |$
$| \begin{array}{r} - 8 & - 4 \\ - 32 & 16 \end{array} |$ $| \begin{array}{r} - 8 & - 4 \\ - 32 & 16 \end{array} |$
$| \begin{array}{r} 43 & - 7 \\ - 81 & 16 \end{array} |$ $| \begin{array}{r} 43 & - 7 \\ - 81 & 16 \end{array} |$
$| \begin{array}{c} 2 & a - 1 \\ a + 2 & a \end{array} |$ $| \begin{array}{c} 2 & a - 1 \\ a + 2 & a \end{array} |$
$| \begin{array}{c} x + y & y - x \\ 2 x & 2 y \end{array} |$ $| \begin{array}{c} x + y & y - x \\ 2 x & 2 y \end{array} |$

In Exercises 19–28, solve the given systems of equations by determinants. (These are the same as those for Exercises 15–24 of Section 5.3.)

$\begin{array}{l} x + 2 y = 5 \\ x - 2 y = 1 \end{array}$ $\begin{array}{l} x + 2 y = 5 \\ x - 2 y = 1 \end{array}$
$\begin{array}{l} x + 3 y = 7 \\ 2 x + 3 y = 5 \end{array}$ $\begin{array}{l} x + 3 y = 7 \\ 2 x + 3 y = 5 \end{array}$
$\begin{array}{l} 2 x - 3 y = 4 \\ 2 x + y = - 4 \end{array}$ $\begin{array}{l} 2 x - 3 y = 4 \\ 2 x + y = - 4 \end{array}$
$\begin{array}{l} R - 4 r = 17 \\ 4 r + 3 R = 3 \end{array}$ $\begin{array}{l} R - 4 r = 17 \\ 4 r + 3 R = 3 \end{array}$
$\begin{array}{l} 12 t + 9 y = 14 \\ 6 t = 7 y - 16 \end{array}$ $\begin{array}{l} 12 t + 9 y = 14 \\ 6 t = 7 y - 16 \end{array}$
$\begin{array}{l} 3 x - y = 3 \\ 4 x = 3 y + 14 \end{array}$ $\begin{array}{l} 3 x - y = 3 \\ 4 x = 3 y + 14 \end{array}$
$\begin{array}{l} v + 2 t = 7 \\ 2 v + 4 t = 9 \end{array}$ $\begin{array}{l} v + 2 t = 7 \\ 2 v + 4 t = 9 \end{array}$
$\begin{array}{l} 3 x - y = 5 \\ 3 y - 9 x = - 15 \end{array}$ $\begin{array}{l} 3 x - y = 5 \\ 3 y - 9 x = - 15 \end{array}$
$\begin{array}{l} 2 x - 3 y - 4 = 0 \\ 3 x + 2 = 2 y \end{array}$ $\begin{array}{l} 2 x - 3 y - 4 = 0 \\ 3 x + 2 = 2 y \end{array}$
$\begin{array}{l} 3 i_{1} + 5 = - 4 i_{2} \\ 3 i_{2} = 5 i_{1} - 2 \end{array}$ $\begin{array}{l} 3 i_{1} + 5 = - 4 i_{2} \\ 3 i_{2} = 5 i_{1} - 2 \end{array}$

In Exercises 29–36, solve the given systems of equations by determinants. All numbers are approximate. (Exercises 29–32 are the same as Exercises 37–40 of Section 5.3.)

$\begin{array}{l} 0.3 x - 0.7 y = 0.4 \\ 0.2 x + 0.5 y = 0.7 \end{array}$ $\begin{array}{l} 0.3 x - 0.7 y = 0.4 \\ 0.2 x + 0.5 y = 0.7 \end{array}$
$\begin{array}{l} 250 R + 225 Z = 400 \\ 375 R - 675 Z = 325 \end{array}$ $\begin{array}{l} 250 R + 225 Z = 400 \\ 375 R - 675 Z = 325 \end{array}$
$\begin{array}{l} 40 s - 30 t = 60 \\ 20 s - 40 t = - 50 \end{array}$ $\begin{array}{l} 40 s - 30 t = 60 \\ 20 s - 40 t = - 50 \end{array}$
$\begin{array}{l} 0.060 x + 0.048 y = - 0.084 \\ 0.065 y - 0.13 x = 0.078 \end{array}$ $\begin{array}{l} 0.060 x + 0.048 y = - 0.084 \\ 0.065 y - 0.13 x = 0.078 \end{array}$
$\begin{array}{l} 301 x - 529 y = 1520 \\ 385 x - 741 y = 2540 \end{array}$ $\begin{array}{l} 301 x - 529 y = 1520 \\ 385 x - 741 y = 2540 \end{array}$
$\begin{array}{l} 0.25 d + 0.63 n = - 0.37 \\ - 0.61 d - 1.80 n = 0.55 \end{array}$ $\begin{array}{l} 0.25 d + 0.63 n = - 0.37 \\ - 0.61 d - 1.80 n = 0.55 \end{array}$
$\begin{array}{l} 1.2 y + 10.8 = - 8.4 x \\ 3.5 x + 4.8 y + 12.9 = 0 \end{array}$ $\begin{array}{l} 1.2 y + 10.8 = - 8.4 x \\ 3.5 x + 4.8 y + 12.9 = 0 \end{array}$
$\begin{array}{l} 6541 x + 4397 y = - 7732 \\ 3309 x - 8755 y = 7622 \end{array}$ $\begin{array}{l} 6541 x + 4397 y = - 7732 \\ 3309 x - 8755 y = 7622 \end{array}$

In Exercises 37–40, answer the given questions about the determinant to the right. $| \begin{array}{l} a & b \\ c & d \end{array} |$ $| \begin{array}{l} a & b \\ c & d \end{array} |$

What is the value of the determinant if $c = d = 0 ?$ $c = d = 0 ?$
What change in value occurs if both the rows and the columns are interchanged?
What is the value of the determinant if $a = k b$ $a = k b$ and $c = k d ?$ $c = k d ?$
How does the value change if a and c are doubled?

In Exercises 41–44, solve the given systems of equations by determinants. All numbers are accurate to at least two significant digits.

The forces acting on a link of an industrial robot are shown in Fig. 5.33. The equations for finding forces $F_{1}$ $F_{1}$ and $F_{2}$ $F_{2}$ are

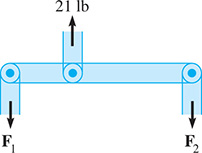
Fig. 5.33

$\begin{array}{l} F_{1} + F_{2} = 21 \\ 2 F_{1} = 5 F_{2} \end{array}$ $\begin{array}{l} F_{1} + F_{2} = 21 \\ 2 F_{1} = 5 F_{2} \end{array}$

Find $F_{1}$ $F_{1}$ and $F_{2} .$ $F_{2} .$
The area of a quadrilateral is

$A = \frac{1}{2} (| \begin{array}{r} x_{0} & x_{1} \\ y_{0} & y_{1} \end{array} | + | \begin{matrix} x_{1} & x_{2} \\ y_{1} & y_{2} \end{matrix} | + | \begin{matrix} x_{2} & x_{3} \\ y_{2} & y_{3} \end{matrix} | + | \begin{matrix} x_{3} & x_{0} \\ y_{3} & y_{0} \end{matrix} |)$ $A = \frac{1}{2} (| \begin{array}{r} x_{0} & x_{1} \\ y_{0} & y_{1} \end{array} | + | \begin{matrix} x_{1} & x_{2} \\ y_{1} & y_{2} \end{matrix} | + | \begin{matrix} x_{2} & x_{3} \\ y_{2} & y_{3} \end{matrix} | + | \begin{matrix} x_{3} & x_{0} \\ y_{3} & y_{0} \end{matrix} |)$

where $(x_{0}, y_{0}), (x_{1}, y_{1}), (x_{2}, y_{2}),$ $(x_{0}, y_{0}), (x_{1}, y_{1}), (x_{2}, y_{2}),$ and $(x_{3}, y_{3})$ $(x_{3}, y_{3})$ are the rectangular coordinates of the vertices of the quadrilateral, listed counterclockwise. (This surveyor’s formula can be generalized to find the area of any polygon.)

A surveyor records the locations of the vertices of a quadrilateral building lot on a rectangular coordinate system as (12.79, 0.00), (67.21, 12.30), (53.05, 47.12), and (10.09, 53.11), where distances are in meters. Find the area of the lot.
An airplane begins a flight with a total of 36.0 gal of fuel stored in two separate wing tanks. During the flight, 25.0% of the fuel in one tank is used, and in the other tank 37.5% of the fuel is used. If the total fuel used is 11.2 gal, the amounts x and y used from each tank can be found by solving the system of equations

$\begin{array}{l} x + y = 36.0 \\ 0.250 x + 0.375 y = 11.2 \end{array}$ $\begin{array}{l} x + y = 36.0 \\ 0.250 x + 0.375 y = 11.2 \end{array}$

Find x and y.
In applying Kirchhoff’s laws (see the chapter introduction; the equations can be found in most physics textbooks) to the electric circuit shown in Fig. 5.34, the following equations are found. Find the indicated currents $I_{1}$ $I_{1}$ and $I_{2}$ $I_{2}$ (in A).

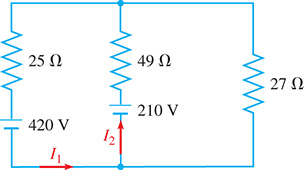
Fig. 5.34

$\begin{array}{l} 52 I_{1} - 27 I_{2} = - 420 \\ - 27 I_{1} + 76 I_{2} = 210 \end{array}$ $\begin{array}{l} 52 I_{1} - 27 I_{2} = - 420 \\ - 27 I_{1} + 76 I_{2} = 210 \end{array}$

In Exercises 45–56, set up appropriate systems of two linear equations in two unknowns and then solve the systems by determinants. All numbers are accurate to at least two significant digits.

A new development has 3-bedroom homes and 4-bedroom homes. The developer’s profit was $25,000 from each 3-br home, and $35,000 from each 4-br home, totaling $6,800,000. Total annual property taxes are $560,000, with $2000 from each 3-br home and $3000 from each 4-br home. How many of each were built?
Two joggers are 2.0 mi apart. If they jog toward each other, they will meet in 12 min. If they jog in the same direction, the faster one will overtake the slower one in 2.0 h. At what rate does each jog?
A shipment of 320 cell phones and radar detectors was destroyed due to a truck accident. On the insurance claim, the shipper stated that each phone was worth $110, each detector was worth $160, and their total value was $40,700. How many of each were in the shipment?
Two types of electromechanical carburetors are being assembled and tested. Each of the first type requires 15 min of assembly time and 2 min of testing time. Each of the second type requires 12 min of assembly time and 3 min of testing time. If 222 min of assembly time and 45 min of testing time are available, how many of each type can be assembled and tested, if all the time is used?
Since ancient times, a rectangle for which the length L is approximately 1.62 times the width w has been considered the most pleasing to view, and is called a golden rectangle. If a painting in the shape of a golden rectangle has a perimeter of 4.20 m, find the dimensions.
The ratio of men to women on a bus was 5/7. Then two women and one man boarded, and the ratio was 7/10. How many men and women were on the bus before the last three passengers boarded?
A machinery sales representative receives a fixed salary plus a sales commission each month. If $6200 is earned on sales of $70,000 in one month and $4700 is earned on sales of $45,000 in the following month, what are the fixed salary and the commission percent?
A moving walkway at an airport is 65.0 m long. A child running at a constant speed takes 20.0 s to run along the walkway in the direction it is moving, and then 52.0 s to run all the way back. What are the speed of the walkway and the speed of the child?
A boat carrying illegal drugs leaves a port and travels at 42 mi/h. A Coast Guard cutter leaves the port 24 min later and travels at 50 mi/h in pursuit of the boat. Find the times each has traveled when the cutter overtakes the boat with drugs. See Fig. 5.35.

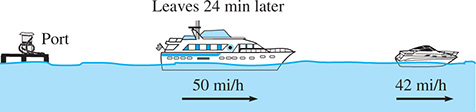
Fig. 5.35
Sterling silver is 92.5% silver and 7.5% copper. One silver-copper alloy is 94.0% silver, and a second silver-copper alloy is 85.0% silver. How much of each should be used in order to make 100 g of sterling silver?
A surveyor measures the angle of elevation to the top of a hill to be 15.5°. He then moves 345 ft closer, on level ground, and remeasures the angle of elevation to be 21.4° (see Fig. 5.36). Find the height h of the hill and the distance d. Hint: Use the tangent function to set up a system of equations.

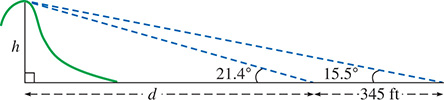
Fig. 5.36

Figure 5.36 Full Alternative Text
The velocity of sound in steel is 15,900 ft/s faster than the velocity of sound in air. One end of a long steel bar is struck, and an instrument at the other end measures the time it takes for the sound to reach it. The sound in the bar takes 0.0120 s, and the sound in the air takes 0.180 s. What are the velocities of sound in air and in steel?

Answers to Practice Exercises

22
2. $x = - 2, y = 3$ $x = - 2, y = 3$
3. $x = $8000, y = $10, 000$ $x = $8000, y = $10, 000$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 5.4 Solving Systems of Two Linear Equations in&#160;Two&#160;Unknowns&#160;by Determinants Solving Systems of Two Linear Equations in Two Unknowns by Determinants

Create new playlist

Sign In

Sign Up

Table of Contents for
5.4 Solving Systems of Two Linear Equations in Two Unknowns by Determinants Solving Systems of Two Linear Equations in Two Unknowns by Determinants