Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

21.8 The Second-degree Equation

Second-degree Equation • Coefficients A, B, C Determine the Type of Curve • Conic Sections

The equations of the circle, parabola, ellipse, and hyperbola are all special cases of the same general equation. In this section, we discuss this equation and how to identify the particular form it takes when it represents a specific type of curve.

Each of these curves can be represented by a second-degree equation of the form

A x^{2} + B x y + C y^{2} + D x + E y + F = 0

$A x^{2} + B x y + C y^{2} + D x + E y + F = 0$ (21.34)

The coefficients of the second-degree equation terms determine the type of curve that results. Recalling the discussions of the general forms of the equations of the circle, parabola, ellipse, and hyperbola from the previous sections of this chapter, Eq. (21.34) represents the indicated curve for given conditions of A, B, and C, as follows:

Another conclusion about Eq. (21.34) is that, if either $D \neq 0$ $D \neq 0$ or $E \neq 0$ $E \neq 0$ (or both), the center of the curve (or vertex of a parabola) is not at the origin. If $B \neq 0,$ $B \neq 0,$ the axis of the curve has been rotated. We have considered only one such case (the hyperbola $x y = c$ $x y = c$ ) so far in this chapter. In the following section, rotation of axes is taken up, and if $B \neq 0,$ $B \neq 0,$ we will see that the type of curve depends on the value $B^{2} - 4 A C .$ $B^{2} - 4 A C .$ The following examples illustrate how the type of curve is identified from the equation according to the five criteria listed above.

EXAMPLE 1 Identify a circle from the equation

The equation $2 x^{2} = 3 - 2 y^{2}$ $2 x^{2} = 3 - 2 y^{2}$ represents a circle. This can be seen by putting the equation in the form of Eq. (21.34). This form is

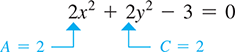
2 x squared + 2 y squared minus 3 = 0. 2 in 2 x squared is labeled, A = 2. And 2 in 2 y squared is labeled, c = 2.

We see that $A = C .$ $A = C .$ Also, since there is no xy-term, we know that $B = 0.$ $B = 0.$ This means that the equation represents a circle. If we write it as $x^{2} + y^{2} = \frac{3}{2},$ $x^{2} + y^{2} = \frac{3}{2},$ we see that it fits the form of Eq. (21.12). The circle is shown in Fig. 21.91.

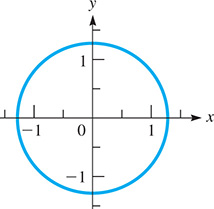
A circle centered at (0, 0) with radius 3 over 2. — Fig. 21.91

EXAMPLE 2 Identify an ellipse from the equation

The equation $3 y^{2} = 6 y - x^{2} + 3$ $3 y^{2} = 6 y - x^{2} + 3$ represents an ellipse. Before analyzing the equation, we should put it in the form of Eq. (21.34). For this equation, this form is

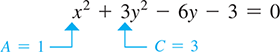
X squared + 3 y squared minus 6 y minus 3 = 0. X squared is labeled, A = 1. 3 and 3 y squared is labeled, c = 3.

Here, we see that $B = 0,$ $B = 0,$ A and C have the same sign, and $A \neq C .$ $A \neq C .$ Therefore, it is an ellipse. The $- 6 y$ $- 6 y$ term indicates that the center of the ellipse is not at the origin. This ellipse is shown in Fig. 21.92.

A horizontal ellipse centered at (0, 1). — Fig. 21.92

EXAMPLE 3 Identify a hyperbola from the equation

Identify the curve represented by $2 x^{2} + 12 x = y^{2} - 14.$ $2 x^{2} + 12 x = y^{2} - 14.$ Determine the appropriate quantities for the curve, and sketch the graph.

Writing this equation in the form of Eq. (21.34), we have

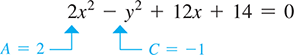
2 x squared minus y squared + 12 x + 14 = 0. 2 in 2 x squared is labeled, A = 2. Y squared is labeled, c = 1.

We identify this equation as representing a hyperbola, because A and C have different signs and $B = 0.$ $B = 0.$ We now write it in the standard form of a hyperbola:

2 x squared + 12 x minus y squared = negative 14.

21.8-2 Full Alternative Text

Thus, we see that the center (h, k) of the hyperbola is the point $(- 3, 0) .$ $(- 3, 0) .$ Also, $a = \sqrt{2}$ $a = \sqrt{2}$ and $b = 2.$ $b = 2.$ This means that the vertices are $(- 3 + \sqrt{2}, 0)$ $(- 3 + \sqrt{2}, 0)$ and $(- 3 - \sqrt{2}, 0),$ $(- 3 - \sqrt{2}, 0),$ and the conjugate axis extends from $(- 3, 2)$ $(- 3, 2)$ to $(- 3, - 2) .$ $(- 3, - 2) .$ Also, $c^{2} = 2 + 4 = 6,$ $c^{2} = 2 + 4 = 6,$ which means that $c = \sqrt{6} .$ $c = \sqrt{6} .$ The foci are $(- 3 + \sqrt{6}, 0)$ $(- 3 + \sqrt{6}, 0)$ and $(- 3 - \sqrt{6}, 0) .$ $(- 3 - \sqrt{6}, 0) .$ The graph is shown in Fig. 21.93.

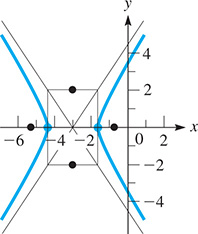
A horizontal hyperbola centered at (negative 3, 0). — Fig. 21.93

Figure 21.93 Full Alternative Text

EXAMPLE 4 Identify a parabola—calculator display

Identify the curve represented by $4 y^{2} - 23 = 4 (4 x + 3 y)$ $4 y^{2} - 23 = 4 (4 x + 3 y)$ and find the appropriate important quantities. Then view it on a calculator.

Writing the equation in the form of Eq. (21.34), we have

4 y^{2} - 16 x - 12 y - 23 = 0

$4 y^{2} - 16 x - 12 y - 23 = 0$

Therefore, we recognize the equation as representing a parabola, because $A = 0$ $A = 0$ and $B = 0.$ $B = 0.$ Now, writing the equation in the standard form of a parabola, we have

21.8-2 Full Alternative Text

We now note that the vertex is $(- 2, 3/2)$ $(- 2, 3/2)$ and that $p = 1.$ $p = 1.$ This means that the focus is $(- 1, 3/2)$ $(- 1, 3/2)$ and the directrix is $x = - 3.$ $x = - 3.$

To view the graph of this equation on a calculator, we first solve the equation for y and get $y = (3 \pm 4 \sqrt{x + 2}) / 2.$ $y = (3 \pm 4 \sqrt{x + 2}) / 2.$ Entering these two functions in the calculator, we get the view shown in Fig. 21.94.

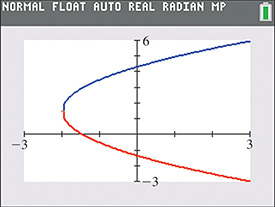
A rightward opening calculator parabola with vertex (negative 2, 3 over 2). The upper and lower halves are represented by different equations. — Fig. 21.94

In Chapter 14, when these curves were first introduced, they were referred to as conic sections. If a plane is passed through a cone, the intersection of the plane and the cone results in one of these curves; the curve formed depends on the angle of the plane with respect to the axis of the cone. This is shown in Fig. 21.95.

Diagrams of conic sections. — Fig. 21.95

Figure 21.95 Full Alternative Text

Exercises 21.8

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the indicated problem.

In Example 1, change the $-$ $-$ before the $2 y^{2}$ $2 y^{2}$ to $+$ $+$ and then determine what type of curve is represented.
In Example 3, change $y^{2} - 14$ $y^{2} - 14$ to $14 - y^{2}$ $14 - y^{2}$ and then determine what type of curve is represented.

In Exercises 3–24, identify each of the equations as representing either a circle, a parabola, an ellipse, a hyperbola, or none of these.

$x^{2} + 2 y^{2} - 2 = 0$ $x^{2} + 2 y^{2} - 2 = 0$
$x^{2} - y - 5 = 0$ $x^{2} - y - 5 = 0$
$2 x^{2} - y^{2} - 1 = 0$ $2 x^{2} - y^{2} - 1 = 0$
$y (y + x^{2}) = 4 (x + y^{2})$ $y (y + x^{2}) = 4 (x + y^{2})$
$8 x^{2} + 2 y^{2} = 6 y (1 - y)$ $8 x^{2} + 2 y^{2} = 6 y (1 - y)$
$x (x - 3) = y (1 - 2 y^{2})$ $x (x - 3) = y (1 - 2 y^{2})$
$2.2 x^{2} - (x + y) = 1.6$ $2.2 x^{2} - (x + y) = 1.6$
$2 x^{2} + 4 y^{2} = y + 2 x$ $2 x^{2} + 4 y^{2} = y + 2 x$
$x^{2} = (y - 1) (y + 1)$ $x^{2} = (y - 1) (y + 1)$
$3.2 x^{2} = 2.1 y (1 - 2 y)$ $3.2 x^{2} = 2.1 y (1 - 2 y)$
$36 x^{2} = 12 y (1 - 3 y) + 1$ $36 x^{2} = 12 y (1 - 3 y) + 1$
$y = 3 (1 - 2 x) (1 + 2 x)$ $y = 3 (1 - 2 x) (1 + 2 x)$
$y (3 - 2 x) = x (5 - 2 y)$ $y (3 - 2 x) = x (5 - 2 y)$
$x (13 - 5 x) = 5 y^{2}$ $x (13 - 5 x) = 5 y^{2}$
$2 x y + x - 3 y = 6$ $2 x y + x - 3 y = 6$
${(y + 1)}^{2} = x^{2} + y^{2} - 1$ ${(y + 1)}^{2} = x^{2} + y^{2} - 1$
$2 x (x - y) = y (3 + y - 2 x)$ $2 x (x - y) = y (3 + y - 2 x)$
$15 x^{2} = x (x - 12) + 4 y (y - 6)$ $15 x^{2} = x (x - 12) + 4 y (y - 6)$
${(x + 1)}^{2} + {(y + 1)}^{2} = 2 (x + y + 1)$ ${(x + 1)}^{2} + {(y + 1)}^{2} = 2 (x + y + 1)$
${(2 x + y)}^{2} = 4 x (y - 2) - 16$ ${(2 x + y)}^{2} = 4 x (y - 2) - 16$
$x (y - x) = x^{2} + x (y + 1) - y^{2} + 1$ $x (y - x) = x^{2} + x (y + 1) - y^{2} + 1$
$4 x (x - 1) = 2 x^{2} - 2 y^{2} + 3$ $4 x (x - 1) = 2 x^{2} - 2 y^{2} + 3$

In Exercises 25–30, identify the curve represented by each of the given equations. Determine the appropriate important quantities for the curve and sketch the graph.

$x^{2} = 8 (y - x - 2)$ $x^{2} = 8 (y - x - 2)$
$x^{2} = 6 x - 4 y^{2} - 1$ $x^{2} = 6 x - 4 y^{2} - 1$
$y^{2} = 2 (x^{2} - 2 x - 2 y)$ $y^{2} = 2 (x^{2} - 2 x - 2 y)$
$4 x^{2} + 4 = 9 - 8 x - 4 y^{2}$ $4 x^{2} + 4 = 9 - 8 x - 4 y^{2}$
$y^{2} + 42 = 2 x (10 - x)$ $y^{2} + 42 = 2 x (10 - x)$
$x^{2} - 4 y = y^{2} + 4 (1 - x)$ $x^{2} - 4 y = y^{2} + 4 (1 - x)$

In Exercises 31–36, identify the type of curve for each equation, and then view it on a calculator.

$x^{2} + 2 y^{2} - 4 x + 12 y + 14 = 0$ $x^{2} + 2 y^{2} - 4 x + 12 y + 14 = 0$
$4 y^{2} - x^{2} + 40 y - 4 x + 60 = 0$ $4 y^{2} - x^{2} + 40 y - 4 x + 60 = 0$
$4 (y^{2} - 4 x - 2) = 5 (4 y - 5)$ $4 (y^{2} - 4 x - 2) = 5 (4 y - 5)$
$2 (2 x^{2} - y) = 8 - y^{2}$ $2 (2 x^{2} - y) = 8 - y^{2}$
$4 (y^{2} + 6 y + 1) = x (x - 4) - 24$ $4 (y^{2} + 6 y + 1) = x (x - 4) - 24$
$8 x + 31 - x y = y (y - 2 - x)$ $8 x + 31 - x y = y (y - 2 - x)$

In Exercises 37–40, use the given values to determine the type of curve represented.

For the equation $x^{2} + k y^{2} = a^{2},$ $x^{2} + k y^{2} = a^{2},$ what type of curve is represented if (a) $k = 1,$ $k = 1,$ (b) $k < 0,$ $k < 0,$ and (c) $k > 0 (k \neq 1) ?$ $k > 0 (k \neq 1) ?$
In Eq. (21.34), if $A > C > 0$ $A > C > 0$ and $B = D = E = F = 0,$ $B = D = E = F = 0,$ describe the locus of the equation.
In Eq. (21.34), if $A = B = C = 0, D \neq 0, E \neq 0,$ $A = B = C = 0, D \neq 0, E \neq 0,$ and $F \neq 0,$ $F \neq 0,$ describe the locus of the equation.
In Eq. (21.34), if $A = - C \neq 0, B = D = E = 0$ $A = - C \neq 0, B = D = E = 0$ and $F = C,$ $F = C,$ describe the locus of the equation if $C > 0.$ $C > 0.$

A flashlight emits a cone of light onto the floor. In Exercises 41–44, determine the type of curve for the perimeter of the lighted area on the floor depending on the position of the flashlight and cone as described. See Fig. 21.96.

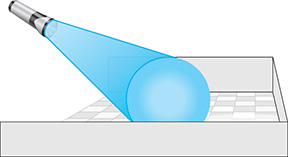
A flashlight shines a beam on a floor at an angle. The beam widens toward its end relative to where it first leaves the flashlight. — Fig. 21.96

The flashlight is directed at the floor and perpendicular to it.
The flashlight is directed toward the floor, but is not perpendicular to it.
The flashlight is parallel to the floor.
The flashlight is directed downward toward the floor such that the upper edge of the cone of light is parallel to the floor.

In Exercises 45–48, determine the type of curve from the given information.

The diagonal brace in a rectangular metal frame is 3.0 cm longer than the length of one of the sides. Determine the type of curve represented by the equation relating the lengths of the sides of the frame.
One circular solar cell has a radius that is 2.0 in. less than the radius r of a second circular solar cell. Determine the type of curve represented by the equation relating the total area A of both cells and r.
A supersonic jet creates a conical shock wave behind it. What type of curve is outlined on the surface of a lake by the shock wave if the jet is flying horizontally?
In Fig. 21.95, if the plane cutting the cones passes through the intersection of the upper and lower cones, what type of curve is the intersection of the plane and cones?

Answers to Practice Exercises

Ellipse
Parabola

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 21.8 The Second-degree Equation

Create new playlist

Sign In

Sign Up

Table of Contents for
21.8 The Second-degree Equation