Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

17.4 Inequalities Involving Absolute Values

Absolute Value Greater Than Given Value • Absolute Value Less Than Given Value

Inequalities involving absolute values are often useful in later topics in mathematics such as calculus and in applications such as the accuracy of measurements. In this section, we show the meaning of such inequalities and how they are solved.

If we wish to write the inequality $| x | > 1$ $| x | > 1$ without absolute-value signs, we must note that we are considering values of x that are numerically larger than 1. Thus, we may write this inequality in the equivalent form $x < - 1$ $x < - 1$ or $x > 1.$ $x > 1.$ We now note that the original inequality, with an absolute-value sign, can be written in terms of two equivalent inequalities, neither involving absolute values. If we are asked to write the inequality $| x | < 1$ $| x | < 1$ without absolute-value signs, we write $- 1 < x < 1,$ $- 1 < x < 1,$ since we are considering values of x numerically less than 1.

Following reasoning similar to this, whenever absolute values are involved in inequalities, the following two relations allow us to write equivalent inequalities without absolute values. For $n > 0,$ $n > 0,$

If | f (x) | > n, then f (x) < - n or f (x) > n .

$If | f (x) | > n, then f (x) < - n or f (x) > n .$ (17.1)

If | f (x) | < n, then - n < f (x) < n .

$If | f (x) | < n, then - n < f (x) < n .$ (17.2)

EXAMPLE 1 Absolute value less than

Solve the inequality $| x - 3 | < 2.$ $| x - 3 | < 2.$

Here, we want values of x such that $x - 3$ $x - 3$ is numerically smaller than 2, or the values of x within 2 units of $x = 3.$ $x = 3.$ These are given by the inequality $1 < x < 5.$ $1 < x < 5.$ Now, using Eq. (17.2), we have

- 2 < x - 3 < 2

$- 2 < x - 3 < 2$

By adding 3 to all three members of this inequality, we have

1 < x < 5

$1 < x < 5$

which is the proper interval. See Fig. 17.30.

A number line for inequality, absolute value of x minus 3, < 2. Open circles are at 1 and 5, and a closed circle is at 3. The open circles are 2 units from 3. — Fig. 17.30

EXAMPLE 2 Absolute value greater than

Solve the inequality $| 2 x - 1 | > 5.$ $| 2 x - 1 | > 5.$

By using Eq. (17.1), we have

2 x - 1 < - 5 or 2 x - 1 > 5

$2 x - 1 < - 5 or 2 x - 1 > 5$

Completing the solution, we have

\begin{array}{rcrl} 2 x < - 4 & or & 2 x > 6 & add 1 to each member \\ x < - 2 & x > 3 & divide each member by 2 \end{array}

$\begin{array}{rcrl} 2 x < - 4 & or & 2 x > 6 & add 1 to each member \\ x < - 2 & x > 3 & divide each member by 2 \end{array}$

This means that the given inequality is satisfied for $x < - 2$ $x < - 2$ or for $x > 3.$ $x > 3.$ The solution is shown in Fig. 17.31.

NOTE

[We must be very careful to remember that we cannot write this as $3 < x < - 2.$ $3 < x < - 2.$ ]

A number line with an open circle at negative 2 and shading to the left, and an open circle at 3 with shading to the right. — Fig. 17.31

The meaning of this inequality is that the numerical value of $2 x - 1$ $2 x - 1$ is greater than 5. By considering values in these intervals, we can see that this is true for values of x less than $- 2$ $- 2$ or greater than 3.

EXAMPLE 3 Absolute value greater than or equal to

Solve the inequality $2 | \frac{2 x}{3} + 1 | \geq 4.$ $2 | \frac{2 x}{3} + 1 | \geq 4.$

The solution is as follows:

\begin{array}{l} \begin{array}{rcl} 2 | \frac{2 x}{3} + 1 | & \geq & 4 & original inequality \\ | \frac{2 x}{3} + 1 | & \geq & 2 & \begin{array}{l} divide each member by 2 to \\ isolate the absolute value \end{array} \end{array} \\ \begin{array}{rclcrcl} \frac{2 x}{3} + 1 & \leq & - 2 & or & \frac{2 x}{3} + 1 & \geq & 2 & using Eq . (17.1) \\ 2 x + 3 & \leq & - 6 & 2 x + 3 & \geq & 6 \\ 2 x & \leq & - 9 & 2 x & \geq & 3 \\ x & \leq & - \frac{9}{2} & x & \geq & \frac{3}{2} & solution \end{array} \end{array}

$\begin{array}{l} \begin{array}{rcl} 2 | \frac{2 x}{3} + 1 | & \geq & 4 & original inequality \\ | \frac{2 x}{3} + 1 | & \geq & 2 & \begin{array}{l} divide each member by 2 to \\ isolate the absolute value \end{array} \end{array} \\ \begin{array}{rclcrcl} \frac{2 x}{3} + 1 & \leq & - 2 & or & \frac{2 x}{3} + 1 & \geq & 2 & using Eq . (17.1) \\ 2 x + 3 & \leq & - 6 & 2 x + 3 & \geq & 6 \\ 2 x & \leq & - 9 & 2 x & \geq & 3 \\ x & \leq & - \frac{9}{2} & x & \geq & \frac{3}{2} & solution \end{array} \end{array}$

This solution is shown in Fig. 17.32. Note that the sign of equality does not change the method of solution. It simply indicates that $- \frac{9}{2}$ $- \frac{9}{2}$ and $\frac{3}{2}$ $\frac{3}{2}$ are included in the solution.

A number line with a closed circle at negative 9 over 2 and shading to the left, and a closed circle at 3 over 2 with shading to the right. — Fig. 17.32

EXAMPLE 4 Absolute value less than

Solve the inequality $| 3 - 2 x | < 3.$ $| 3 - 2 x | < 3.$

We have the following solution.

\begin{array}{rcl} | 3 - 2 x | & < & 3 & original inequality \\ - 3 < 3 - 2 x & < & 3 & using Eq . (17.2) \\ - 6 < - 2 x & < & 0 \\ 3 > x & > & 0 & divide by - 2 and reverse signs of inequality \\ 0 < x & < & 3 & solution \end{array}

$\begin{array}{rcl} | 3 - 2 x | & < & 3 & original inequality \\ - 3 < 3 - 2 x & < & 3 & using Eq . (17.2) \\ - 6 < - 2 x & < & 0 \\ 3 > x & > & 0 & divide by - 2 and reverse signs of inequality \\ 0 < x & < & 3 & solution \end{array}$

The meaning of the inequality is that the numerical value of $3 - 2 x$ $3 - 2 x$ is less than 3. This is true for values of x between 0 and 3. The solution is shown in Fig. 17.33.

A number line with shading between open circles at 0 and 3. — Fig. 17.33

EXAMPLE 5 Absolute value—fire hose pressure

The pressure from a fire truck pump is $120 lb / in .^{2}$ $120 lb / in .^{2}$ with a possible variation of $\pm 10 lb / in .^{2}$ $\pm 10 lb / in .^{2}$ Express this pressure p in terms of an inequality with absolute values.

This statement tells us that the pressure is no less than $110 lb / in .^{2}$ $110 lb / in .^{2}$ and no more than $130 lb / in .^{2} .$ $130 lb / in .^{2} .$ Another way of stating this is that the numerical difference between the actual value of p (unknown exactly) and the measured value, $120 lb / in .^{2},$ $120 lb / in .^{2},$ is less than or equal to $10 lb / in .^{2} .$ $10 lb / in .^{2} .$ Using an absolute value inequality, this is written as

| p - 120 | \leq 10

$| p - 120 | \leq 10$

where values are in $lb / in .^{2} .$ $lb / in .^{2} .$

We can see that this is the correct way of writing the inequality by using Eq. (17.2), which gives us

\begin{array}{rcl} - 10 & \leq & p - 120 \leq 10 \\ 110 & \leq & p \leq 130 \end{array}

$\begin{array}{rcl} - 10 & \leq & p - 120 \leq 10 \\ 110 & \leq & p \leq 130 \end{array}$

This verifies that p should not be less than $110 lb / in .^{2}$ $110 lb / in .^{2}$ or more than $130 lb / in .^{2} .$ $130 lb / in .^{2} .$ This solution is shown in Fig. 17.34.

A number line with shading between closed circles at 110 and 120, and shading between closed circles at 110 and 130. — Fig. 17.34

Most calculators can be used to display the solution of an inequality that involves absolute values just as they can display the solutions to other inequalities. Because calculators differ in their operation, check the manual of your calculator to see how an absolute value is entered and displayed. The following example shows the display of the solution of an inequality on a graphing calculator.

EXAMPLE 6 Calculator solution of absolute-value inequality

Display the solution to the inequality $| \frac{x}{2} - 3 | < 1$ $| \frac{x}{2} - 3 | < 1$ on a calculator.

On the calculator, set $y_{1} = abs (x / 2 - 3) < 1$ $y_{1} = abs (x / 2 - 3) < 1$ and obtain the display shown in Fig. 17.35. From this display, we see that the solution is $4 < x < 8.$ $4 < x < 8.$

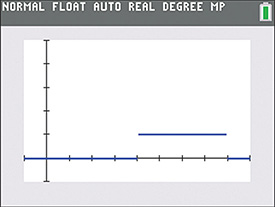
A line segment goes from (4, 1) to (8, 1). — Fig. 17.35

EXERCISES 17.4

In Exercises 1 and 2, make the given changes in the indicated examples of this section and then solve the resulting inequalities.

In Example 2, change the $>$ $>$ to $<,$ $<,$ solve the resulting inequality, and graph the solution.
In Example 4, change the $<$ $<$ to $>,$ $>,$ solve the resulting inequality, and graph the solution.

In Exercises 3–24, solve the given inequalities. Graph each solution.

$| x - 4 | < 1$ $| x - 4 | < 1$
$| x + 4 | < 6$ $| x + 4 | < 6$
$| 5 x + 4 | > 6$ $| 5 x + 4 | > 6$
$| \frac{1}{2} N - 1 | > 3$ $| \frac{1}{2} N - 1 | > 3$
$1 + | 6 x - 5 | \leq 5$ $1 + | 6 x - 5 | \leq 5$
$| 30 - 42 x | \leq 0$ $| 30 - 42 x | \leq 0$
$| 3 - 4 x | > 3$ $| 3 - 4 x | > 3$
$3 + | 3 x + 1 | \geq 5$ $3 + | 3 x + 1 | \geq 5$
$| \frac{t + 1}{5} | < 5$ $| \frac{t + 1}{5} | < 5$
$| \frac{2 x - 9}{4} | < 3$ $| \frac{2 x - 9}{4} | < 3$
$| 20 x + 85 | \leq 46$ $| 20 x + 85 | \leq 46$
$| 2.6 x - 9.1 | > 10.4$ $| 2.6 x - 9.1 | > 10.4$
$2 | x - 24 | > 84$ $2 | x - 24 | > 84$
$3 | 4 - 3 x | \leq 10$ $3 | 4 - 3 x | \leq 10$
$8 + 3 | 3 - 2 x | < 11$ $8 + 3 | 3 - 2 x | < 11$
$5 - 4 | 1 - 7 x | > 13$ $5 - 4 | 1 - 7 x | > 13$
$4 | 2 - 5 x | \geq 6$ $4 | 2 - 5 x | \geq 6$
$2.5 | 7.1 - 2.0 x | \leq 6.5$ $2.5 | 7.1 - 2.0 x | \leq 6.5$
$| \frac{3 R}{5} + 1 | < 8$ $| \frac{3 R}{5} + 1 | < 8$
$| \frac{4 x}{3} - 5 | \geq 7$ $| \frac{4 x}{3} - 5 | \geq 7$
$| 6.5 - \frac{x}{2} | \geq 2.3$ $| 6.5 - \frac{x}{2} | \geq 2.3$
$| \frac{2 w + 5}{w + 1} | \geq 1$ $| \frac{2 w + 5}{w + 1} | \geq 1$

In Exercises 25–28, solve the given inequalities by displaying the solutions on a calculator. See Example 6.

$| 2 x - 5 | < 3$ $| 2 x - 5 | < 3$
$2 | 6 - T | > 5$ $2 | 6 - T | > 5$
$| 4 - \frac{x}{2} | \geq 1$ $| 4 - \frac{x}{2} | \geq 1$
$| \frac{y}{3} + 12 | - 3 \leq 22$ $| \frac{y}{3} + 12 | - 3 \leq 22$

In Exercises 29–32, solve the given quadratic inequalities. Check each by displaying the solution on a calculator.

$| x^{2} + x - 4 | > 2$ $| x^{2} + x - 4 | > 2$

[After using Eq. (17.1), you will have two inequalities. The solution includes the values of x that satisfy either of the inequalities.]
$| x^{2} + 3 x - 1 | > 3$ $| x^{2} + 3 x - 1 | > 3$ (See Exercise 29.)
$| x^{2} + x - 4 | < 2$ $| x^{2} + x - 4 | < 2$

[Use Eq. (17.2), and then treat the resulting inequality as two inequalities of the form $f (x) > - n$ $f (x) > - n$ and $f (x) < n .$ $f (x) < n .$ The solution includes the values of x that satisfy both of the inequalities.]
$| x^{2} + 3 x - 1 | < 3$ $| x^{2} + 3 x - 1 | < 3$ (See Exercise 31.)

In Exercises 33–40, solve the given problems.

Solve for x if $| x | < a$ $| x | < a$ and $a \leq 0.$ $a \leq 0.$ Explain.
Solve for x if $| x - 1 | < 4$ $| x - 1 | < 4$ and $x \geq 0.$ $x \geq 0.$
Solve for x: $| x - 5 | < 3$ $| x - 5 | < 3$ and $| x - 7 | < 2.$ $| x - 7 | < 2.$
Solve for $x : 1 < | x - 2 | < 3.$ $x : 1 < | x - 2 | < 3.$
If $| x - 1 | < 4,$ $| x - 1 | < 4,$ find a and b if $a < x + 4 < b .$ $a < x + 4 < b .$
Solve for x if $| x - 1 | > 4$ $| x - 1 | > 4$ and $| x - 3 | < 5$ $| x - 3 | < 5$ .
The thickness t (in km) of Earth’s crust varies and can be described as $| t - 27 | \leq 23.$ $| t - 27 | \leq 23.$ What are the minimum and maximum values of the thickness of Earth’s crust?
A motorist notes the gasoline gauge and estimates there are about 9 gal in the tank, but knows the estimate may be off by as much as 1 gal. This means we can write $| n - 9 | \leq 1,$ $| n - 9 | \leq 1,$ where n is the number of gallons in the tank. Using this inequality, what distance can the car go on this gas, if it gets 25 mi/gal?

In Exercises 41–48, use inequalities involving absolute values to solve the given problems.

The production p (in barrels) of oil at a refinery is estimated at $2, 000, 000 \pm 200, 000.$ $2, 000, 000 \pm 200, 000.$ Express p using an inequality with absolute values and describe the production in a verbal statement.
According to the Waze navigation app, the time required for a driver to reach his destination is 52 min. If this time is accurate to $\pm 3$ $\pm 3$ min, express the travel time t using an inequality with absolute values.
The temperature T (in °C) at which a certain machine can operate properly is $70 \pm 20.$ $70 \pm 20.$ Express the temperature T for proper operation using an inequality with absolute values.
The Mach number M of a moving object is the ratio of its velocity v to the velocity of sound $v_{s},$ $v_{s},$ and $v_{s}$ $v_{s}$ varies with temperature. A jet traveling at 1650 km/h changes its altitude from 500 m to 5500 m. At 500 m (with the temperature at 27° C), $v_{s} = 1250 km / h,$ $v_{s} = 1250 km / h,$ and at $5500 m (- 3 ° C), v_{s} = 1180 km / h .$ $5500 m (- 3 ° C), v_{s} = 1180 km / h .$ Express the range of M, using an inequality with absolute values.
The diameter d of a certain type of tubing is 3.675 cm with a tolerance of 0.002 cm. Express this as an inequality with absolute values.
The velocity v (in ft/s) of a projectile launched upward from the ground is given by $v = - 32 t + 56,$ $v = - 32 t + 56,$ where t is given in seconds. Given that $speed = | velocity |,$ $speed = | velocity |,$ find the times at which the speed is greater than 8 ft/s.
The voltage v in a certain circuit is given by $v = 6.0 - 200 i,$ $v = 6.0 - 200 i,$ where i is the current (in A). For what values of the current is the absolute value of the voltage less than 2.0 V?
A rocket is fired from a plane flying horizontally at 9000 ft. The height h (in ft) of the rocket above the plane is given by $h = 560 t - 16 t^{2},$ $h = 560 t - 16 t^{2},$ where t is the time (in s) of flight of the rocket. When is the rocket more than 4000 ft above or below the plane? See Fig. 17.36.

Fig. 17.36

Answers to Practice Exercises

$x < 3$ $x < 3$ or $x > 6$ $x > 6$
$2 \leq x \leq 6$ $2 \leq x \leq 6$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 17.4 Inequalities Involving Absolute Values

Create new playlist

Sign In

Sign Up

Table of Contents for
17.4 Inequalities Involving Absolute Values